Source code (c++, python or opengl) and STL models: [click here to download]

Demonstration (video): [View]

Paper (PDF): [View]

The algorithm is described in detail in our paper (please cite it whenever the code/database is used):

An Optimal Algorithm for 3D Triangle Mesh Slicing
R. Minetto, N. Volpato, J. Stolfi, R.M.M.H. Gregori and M.V.G. da Silva, pp. 1-10, 2017
Computer-Aided Design (CAD), Elsevier.
http://dx.doi.org/10.1016/j.cad.2017.07.001

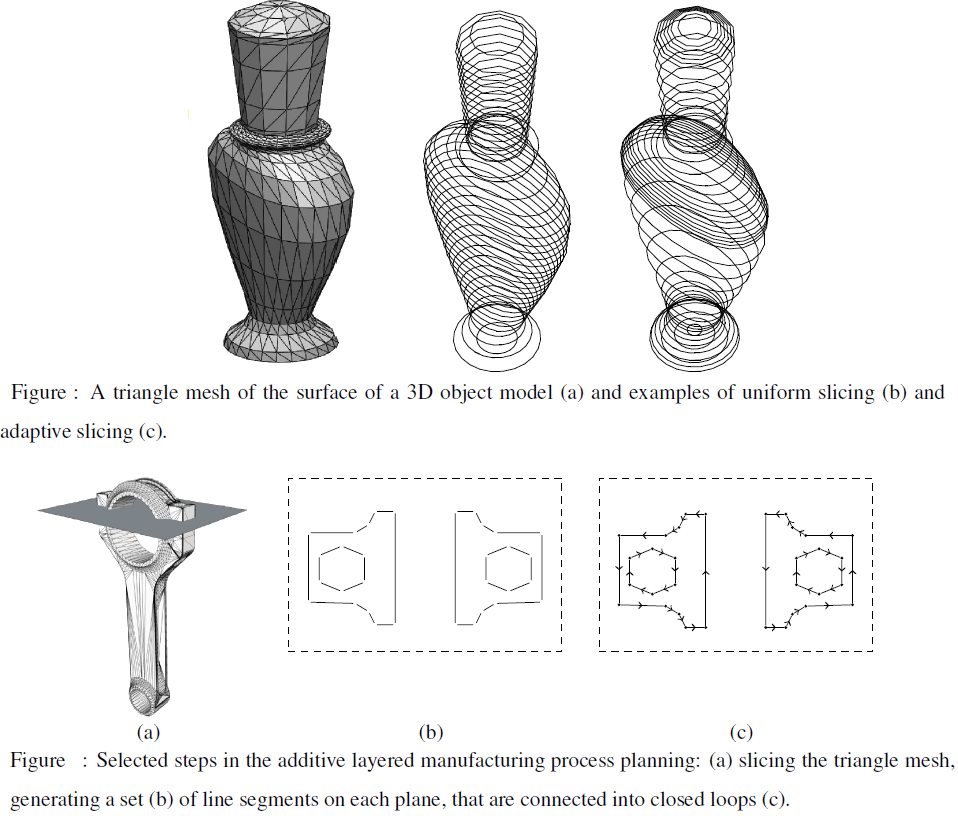
We describe an algorithm for slicing an unstructured triangular mesh model by a series of parallel planes. We prove that the algorithm is asymptotically optimal: its time complexity is O(n log k + k + m) for irregularly spaced slicing planes, where n is the number of triangles, k is the number of slicing planes, and m is the number of triangle-plane intersections segments. The time complexity reduces to O(n + k + m) if the planes are uniformly spaced or the triangles of the mesh are given in the proper order. We also describe an asymptotically optimal linear time algorithm for constructing a set of polygons from the unsorted lists of line segments produced by the slicing step. The proposed algorithms are compared both theoretically and experimentally against known methods in the literature.