Teoria da Computação (ICSA31)

• Base: [HMU06] Sec. 1.5; [Pap93] Cap. 1
• Exercícios: 1–3

DEFINIÇÃO 1.1. Um alfabeto é um conjunto finito não-vazio de símbolos.

Exemplos:

\begin{equation*} \begin{gathered} \{0,1\}\quad\{a\}\quad\{b,r,a,s,i,l\}\\ \{0,1,2,3,4,5,6,7,8,9\}\quad\{?,\#\} \end{gathered} \end{equation*}

DEFINIÇÃO 1.2. Uma palavra (ou string) \(w\) sobre um alfabeto \(\Sigma\) é uma sequência finita de símbolos de \(\Sigma\), sendo o comprimento de \(w\) denotado por \(\lvert w\rvert\). Em particular, a palavra vazia (i.e. a palavra cujo comprimento é \(0\)) é denotada por \(\def\upeps{\text{ε}}\upeps\).

Sendo \(k\) um inteiro não-negativo e \(\Sigma\) um alfabeto, \(\Sigma^k\) denota o conjunto das palavras sobre \(\Sigma\) com comprimento exatamente \(k\). Adicionalmente, \(\Sigma^{\ast}\) denota o conjunto de todas as palavras sobre \(\Sigma\), ou seja,

\begin{equation} \Sigma^{\ast}=\bigcup_{k\geq 0}\Sigma^k\,, \end{equation}

assim como \(\Sigma^+\) denota o conjunto de todas as palavras de comprimento não nulo sobre \(\Sigma\), isto é,

\begin{equation} \Sigma^+=\bigcup_{k> 0}\Sigma^k=\Sigma^{\ast}\setminus\{\upeps\}\,. \end{equation}

Ainda, para cada símbolo \(s\in\Sigma\) e cada palavra \(w\in\Sigma^{\ast}\), escrevemos \(\#s(w)\) para denotar o número de ocorrências do símbolo \(s\) em \(w\).

Sendo \(w_1\) e \(w_2\), a concatenação de \(w_1\) com \(w_2\) é denotada por \(w_1\cdot w_2\), ou simplesmente por \(w_1w_2\).

DEFINIÇÃO 1.3. Uma linguagem é um conjunto de palavras sobre um alfabeto \(\Sigma\), i.e. um subconjunto de \(\Sigma^{\ast}\).

DEFINIÇÃO 1.4. Sendo \(\Sigma\) um alfabeto e \(L\subseteq\Sigma^{\ast}\), o complemento de \(L\), ou a linguagem complementar de \(L\), é a linguagem \(\Sigma^{\ast}\setminus L\).

DEFINIÇÃO 1.5. Sendo \(\Sigma\) um alfabeto e \(X\) um conjunto enumerável, uma função de codificação é uma função injetiva \(\def\funto#1#2#3{{#1}\colon{#2}\to{#3}}\funto{\langle\rangle}{X}{\Sigma^{\ast}}\).

DEFINIÇÃO 1.6. Um problema computacional é uma tripla \(\Pi=(\mathscr I, \mathscr S, \rho)\) em que:

• \(\mathscr I\) é um conjunto enumerável, o conjunto das instâncias de \(\Pi\);
• \(\mathscr S\) é um conjunto enumerável, o conjunto das soluções de \(\Pi\);
• \(\rho\subseteq \mathscr I\times \mathscr S\) é uma relação binária, a relação que associa a cada instância suas respectivas soluções.

DEFINIÇÃO 1.7. Um problema computacional \(\Pi=(\mathscr I, \mathscr S, \rho)\) é dito um problema de decisão se \(\mathscr S=\{0,1\}\) e se \(\rho\) é uma função. Neste caso, os elementos de \(\rho^{-1}(1)\) são as instâncias positivas de \(\Pi\), enquanto que os elementos de \(\rho^{-1}(0)\) são as instâncias negativas.

DEFINIÇÃO 1.8. Sendo \(\Pi=(\mathscr I, \mathscr S, \rho)\) um problema de decisão, \(\Sigma\) um alfabeto, e \(\funto{\langle\rangle}{\mathscr I\cup\mathscr S}{\Sigma^{\ast}}\) uma função de codificação, a linguagem associada a \(\Pi\) é a linguagem das instâncias positivas de \(\Pi\) codificadas, isto é,

\begin{equation} L=\{\langle x\rangle\mathbin{:}x\in \rho^{-1}(1)\}\,. \end{equation}

• Base: [HMU06] Sec. 2.1–2.3, Cap. 3; [Sip12] Cap. 1
• Exercícios: 4–8

DEFINIÇÃO 2.1. Sendo \(L_1\) e \(L_2\) duas linguagens sobre um alfabeto \(\Sigma\), a concatenação de \(L_1\) com \(L_2\) é a linguagem

\begin{equation*} \def\bydef{\mathbin{:=}}L_1L_2\bydef\{w_1w_2\mathbin : w_1\in L_1\text{ e }w_2\in L_2\}\,. \end{equation*}

DEFINIÇÃO 2.2. Sendo \(L\) uma linguagem sobre um alfabeto \(\Sigma\) e \(k\) um inteiro não-negativo qualquer, definimos

\begin{equation*} L^k\bydef\{w_1w_2\dotsb w_k\mathbin : w_i\in L\text{ para todo }i\in\{1,\dotsc,k\}\}\,. \end{equation*}

Observe que, como \(\upeps\) é o elemento neutro da operação de concatenação, temos que \(L^0=\{\upeps\}\) para toda linguagem \(L\).

DEFINIÇÃO 2.3. Sendo \(L\) uma linguagem sobre um alfabeto \(\Sigma\), o fecho Kleene de \(L\) é a linguagem

\begin{equation*} L^{\ast}\bydef \bigcup_{k\geq 0} L^k\,. \end{equation*}

DEFINIÇÃO 2.4 (Expressão regular). Seja \(\Sigma\) um alfabeto.

1. A expressão \(\boldsymbol{\emptyset}\) é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\boldsymbol{\emptyset})\bydef\emptyset\). A expressão \(\def\bupeps{\text{𝛆}}\bupeps\) também é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\bupeps)\bydef\{\upeps\}\).
2. Para cada \(s\in \Sigma\), a expressão \(\boldsymbol s\) é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\boldsymbol s)\bydef\{s\}\).
3. Sendo \(\varphi_1\) e \(\varphi_2\) duas expressões regulares sobre \(\Sigma\), a expressão \(\varphi_1\mathbin{\boldsymbol+}\varphi_2\) é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\varphi_1\mathbin{\boldsymbol+}\varphi_2)\bydef L(\varphi_1)\cup L(\varphi_2)\).
4. Sendo \(\varphi_1\) e \(\varphi_2\) duas expressões regulares sobre \(\Sigma\), a expressão \(\varphi_1\mathbin{\boldsymbol{\cdot}}\varphi_2\), ou simplesmente \(\varphi_1\varphi_2\), é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\varphi_1\varphi_2)\bydef L(\varphi_1)L(\varphi_2)\).
5. Sendo \(\varphi\) uma expressão regular sobre \(\Sigma\), a expressão \(\varphi^{\boldsymbol\ast}\) é uma expressão regular sobre \(\Sigma\), a qual representa a linguagem \(L(\varphi^{\boldsymbol\ast})\bydef (L(\varphi))^{\ast}\).

Em expressões regulares, convencionamos a seguinte precedência dos operadores:

1. o operador de estrela Kleene (\(^{\boldsymbol{\ast}}\));
2. o operador de concatenação (\(\boldsymbol{\cdot}\));
3. o operador de união (\(\boldsymbol+\)).

Naturalmente, tal precedência pode ser alterada através do uso de parênteses.

DEFINIÇÃO 2.5. Uma linguagem sobre um alfabeto \(\Sigma\) é dita regular se pode ser representada por uma expressão regular sobre \(\Sigma\).

Exemplos:

• a linguagem \(L\bydef\{w\in\{0,1\}^{\ast}\mathbin{:}\#0(w)\geq 1\}\), i.e. a linguagem das palavras binárias que possuem ao menos um \(0\), a qual pode ser representada pela expressão regular

  \begin{equation*} (\boldsymbol{0+1})^{\boldsymbol{\ast}}\boldsymbol 0(\boldsymbol{0+1})^{\boldsymbol{\ast}}\,; \end{equation*}

• a linguagem das palavras binárias que possuem \(01\) como substring, a qual pode ser representada pela expressão regular

  \begin{equation*} (\boldsymbol{0+1})^{\boldsymbol{\ast}}\boldsymbol{01}(\boldsymbol{0+1})^{\boldsymbol{\ast}}\,; \end{equation*}

• a linguagem \(L\bydef\{\langle 2n\rangle_2\mathbin : n\in\def\bZ{\mathbb Z}\def\bN{{\mathbb Z}_{\geq 0}}\bN\}\), i.e. a linguagem das palavras binárias que codificam os inteiros não-negativos pares segundo o esquema usual de codificação binária em big endian (o esquema segundo o qual o bit mais significativo é o mais à esquerda e segundo o qual não sobram zeros à esquerda na codificação de inteiros positivos), a qual pode ser representada pela expressão regular

  \begin{equation*} \boldsymbol{0+1}(\boldsymbol{0+1})^{\boldsymbol{\ast}}\boldsymbol0\,, \end{equation*}

  ou pela expressão regular equivalente

  \begin{equation*} \bigl(\boldsymbol1(\boldsymbol{0+1})^{\boldsymbol{\ast}}\bigl)^{\boldsymbol{\ast}}\boldsymbol0\,. \end{equation*}

DEFINIÇÃO 2.6. Um autômato finito determinístico (AFD) é uma \(5\)-tupla \((Q, \Sigma,\delta,q_0, F)\) em que:

• \(Q\) é o conjunto de estados do autômato, um conjunto finito e não-vazio;
• \(\Sigma\) é o alfabeto do autômato (finito e não-vazio pela Definição 1.1);
• \(\delta\colon Q\times\Sigma\to Q\) é a função de transição do autômato;
• \(q_0\in Q\) é o estado inicial do autômato;
• \(F\subseteq Q\) é o conjunto de estados finais do autômato.

Como exemplo, apresentamos \(A=(\{q_0,q_F\},\{0,1\},\delta,q_0,\{q_F\})\), sendo \(\delta\) a função de transição definida por:

\((q,s)\)	\(\delta(q,s)\)
\((q_0, 0)\)	\(q_F\)
\((q_0, 1)\)	\(q_0\)
\((q_F, 0)\)	\(q_F\)
\((q_F, 1)\)	\(q_F\)

Observe que a tabela acima é suficiente para descrever \(\delta\), mas insuficiente para descrever \(A\), pois não identifica qual estado de \(A\) é o inicial, nem quais são os finais (tivemos de explicitar tais informações na descrição da tupla ao apresentarmos o autômato). Um jeito mais sucinto e mais completo de descrever o mesmo autômato é através da tabela de transições a seguir, em que o estado inicial é indicado por \(\to\), e os estados finais, por \(\ast\).

	\(0\)	\(1\)
\(\to q_0\)	\(q_F\)	\(q_0\)
\(\ast q_F\)	\(q_F\)	\(q_F\)

DEFINIÇÃO 2.7. O diagrama de transições de um AFD \(A=(Q,\Sigma,\delta,q_0, F)\) é a representação de um grafo dirigido cujos vértices são os estados de \(A\) e, para cada \(q\in Q\) e cada \(s\in \Sigma\), há um arco de \(q\) para \(\delta(q, s)\) rotulado com \(s\). O estado \(q_0\) é identificado por um semiarco chegando no vértice correspondente, assim como cada estado final é identificado circulando-se duplamente o vértice correspondente. Arcos paralelos com diferentes rótulos podem ser representados por um único arco separando-se os rótulos por vírgula.

O autômato \(A\) do nosso exemplo é o autômato representado pelo diagrama de transições a seguir.

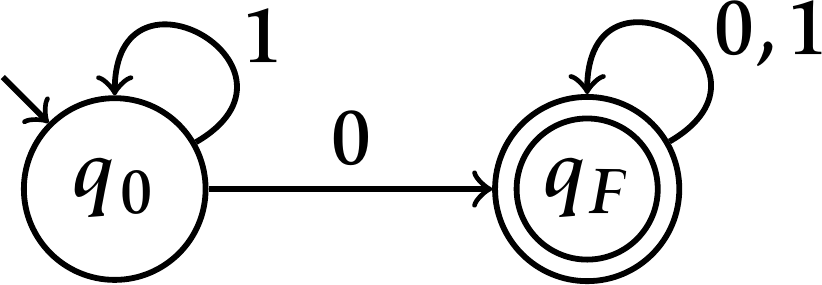
DEFINIÇÃO 2.8. Sendo \(A=(Q, \Sigma,\delta,q_0, F)\) um AFD, a função de transição estendida \(\hat{\delta}\colon Q\times\Sigma^{\ast}\to Q\) de \(A\) é a função definida por:

1. \(\hat{\delta}(q,\upeps) = q\), para todo \(q\in Q\);
2. \(\hat{\delta}(q,sw) = \hat{\delta}(\delta(q,s),w)\), para todo \(q\in Q\), todo \(s\in \Sigma\), e todo \(w\in\Sigma^{\ast}\).

Considerando a palavra \(101\) e o autômato \(A\) do nosso exemplo, temos:

\begin{align*} \hat{\delta}(q_0,101)&=\hat{\delta}(\delta(q_0,1),01)\\ &=\hat{\delta}(q_0,01)\\ &=\hat{\delta}(\delta(q_0,0),1)\\ &=\hat{\delta}(q_F,1)\\ &=\hat{\delta}(\delta(q_F,1),\upeps)\\ &=\hat{\delta}(q_F,\upeps)\\ &=q_F\,. \end{align*}

DEFINIÇÃO 2.9. Dizemos que um AFD \(A=(Q, \Sigma,\delta,q_0, F)\) aceita uma palavra \(x\in \Sigma^{\ast}\) se \(\hat{\delta}(q_0,x)\in F\), e que rejeita \(x\) se \(\hat{\delta}(q_0,x)\notin F\). Ainda, dizemos que o autômato aceita, ou reconhece, uma linguagem \(L\) sobre \(\Sigma\) se, para todo \(x\in \Sigma^{\ast}\), vale que \(A\) aceita \(x\) se e somente se \(x\in L\).

Como por definição a linguagem sobre \(\Sigma^{\ast}\) que um AFD \(A\) aceita é única, usamos \(L(A)\) para denotá-la, chamando-a por vezes de a linguagem do autômato \(A\).

No nosso exemplo, \(L(A)=\{w\in\{0,1\}^{\ast}\mathbin{:}\#0(w)\geq 1\}\).

DEFINIÇÃO 2.10. Um autômato finito não-determinístico (AFN) é uma \(5\)-tupla \((Q, \Sigma,\delta,q_0, F)\) em que:

• \(Q\) é o conjunto de estados do autômato, finito e não-vazio;
• \(\Sigma\) é o alfabeto do autômato;
• \(\delta\colon Q\times\Sigma\to 2^Q\) é a função de transição do autômato, sendo \(2^Q\) o conjunto das partes de \(Q\);
• \(q_0\in Q\) é o estado inicial do autômato;
• \(F\subseteq Q\) é o conjunto de estados finais do autômato.

Como exemplo, apresentamos o autômato \(N=(\{q_0,q_1,q_F\},\{0,1\},\delta,q_0,\{q_F\})\) definido pela seguinte tabela de transições.

	\(0\)	\(1\)
\(\to q_0\)	\(\{q_0,q_1\}\)	\(\{q_0\}\)
\(q_1\)	\(\emptyset\)	\(\{q_F\}\)
\(\ast q_F\)	\(\emptyset\)	\(\emptyset\)

Diagramas de transições são definidos para AFNs de modo análogo a como são definidos para AFDs. Abaixo exibimos o diagrama de transições do autômoto \(N\) do nosso exemplo.

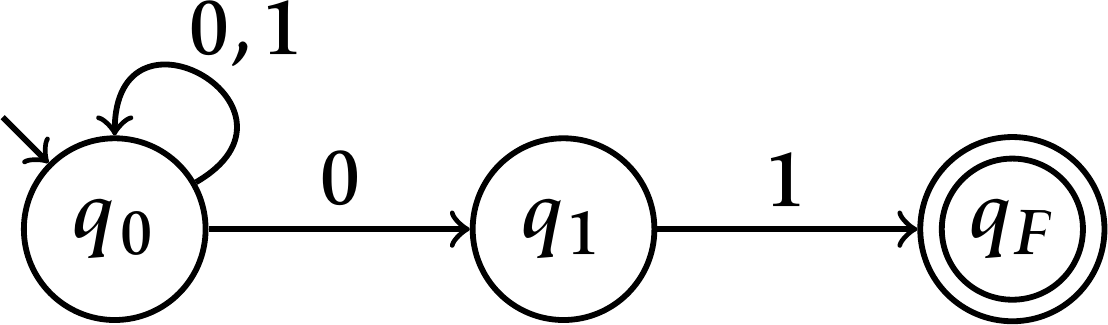
DEFINIÇÃO 2.11. Sendo \(N=(Q, \Sigma,\delta,q_0, F)\) um AFN, a função de transição estendida \(\hat{\delta}\colon Q\times\Sigma^{\ast}\to 2^Q\) de \(N\) é a função definida por:

1. \(\hat{\delta}(q,\upeps) = \{q\}\), para todo \(q\in Q\);
2. \(\hat{\delta}(q,sw) = \bigcup_{p\in \delta(q,s)}\hat{\delta}(p,w)\), para todo \(q\in Q\), todo \(s\in \Sigma\), e todo \(w\in\Sigma^{\ast}\).

Considerando a palavra \(001\) e o autômato \(N\) do nosso exemplo, temos:

\begin{align*} \hat{\delta}(q_0,001)&= \hat{\delta}(q_0,01)\cup\hat{\delta}(q_1,01)\\ &=\hat{\delta}(q_0,1)\cup \hat{\delta}(q_1,1)\cup \emptyset\\ &=\hat{\delta}(q_0,\upeps)\cup\hat{\delta}(q_F,\upeps)\\ &=\{q_0\}\cup\{q_F\}\\ &=\{q_0,q_F\}\,. \end{align*}

DEFINIÇÃO 2.12. Um autômato finito não-determinístico com transições-ε (AFN-ε) é uma \(5\)-tupla \((Q, \Sigma,\delta,q_0, F)\) em que:

• \(Q\) é o conjunto de estados do autômato, finito e não-vazio;
• \(\Sigma\) é o alfabeto do autômato, o qual não pode conter o símbolo especial \(\upeps\);
• \(\delta\colon Q\times(\Sigma\cup\{\upeps\})\to 2^Q\) é a função de transição do autômato;
• \(q_0\in Q\) é o estado inicial do autômato;
• \(F\subseteq Q\) é o conjunto de estados finais do autômato.

Como exemplo, apresentamos o autômato \(E=(\{q_0,q_1,q_2,q_3,q_F,q_G\},\{0,1,{+},{-},{.}\},\delta,q_0,\{q_F,q_G\})\) definido pelo seguinte diagrama de transições.

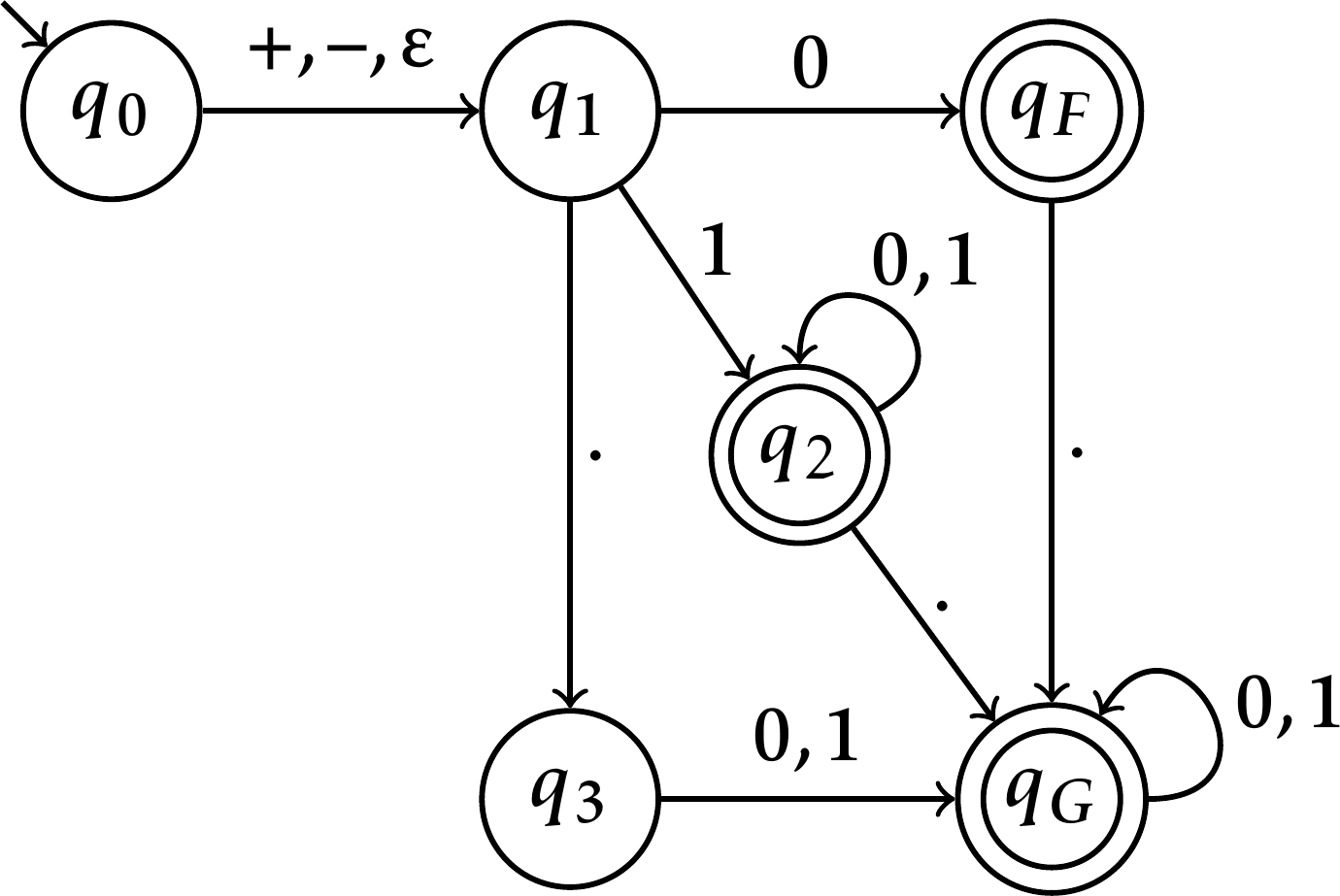
DEFINIÇÃO 2.13. Sendo \(E=(Q, \Sigma,\delta,q_0, F)\) um AFN-ε e \(q\in Q\), o fecho-ε de \(q\) é o conjunto

\begin{equation*} \def\eclose{\mathrm{\upeps c\ell}}\eclose(q)\bydef \{q\}\cup \bigcup_{p\in\delta(q,\upeps)}\eclose(p)\,. \end{equation*}

DEFINIÇÃO 2.14. Sendo \(E=(Q, \Sigma,\delta,q_0, F)\) um AFN-ε, a função de transição estendida \(\hat{\delta}\colon Q\times(\Sigma\cup\{\upeps\})^{\ast}\to 2^Q\) de \(E\) é a função definida por:

1. \(\hat{\delta}(q,\upeps) = \eclose(q)\), para todo \(q\in Q\);
2. \(\hat{\delta}(q,sw) = \bigcup_{p\in\eclose(q)}\bigcup_{r\in \delta(p,s)}\hat{\delta}(r,w)\), para todo \(q\in Q\), todo \(s\in \Sigma\), e todo \(w\in\Sigma^{\ast}\).

Considerando a palavra \(0.1\) e o autômato \(E\) do nosso exemplo, temos:

\begin{align*} \hat{\delta}(q_0,0.1)&= \biggl(\bigcup_{r\in\delta(q_0,0)}\hat{\delta}(r,.1)\biggr) \cup \biggl(\bigcup_{r\in\delta(q_1,0)}\hat{\delta}(r,.1)\biggr)\\ &=\emptyset\cup \hat{\delta}(q_F,.1)\\ &=\bigcup_{r\in\delta(q_F,{.})}\hat{\delta}(r,1)\\ &=\hat{\delta}(q_G,1)\\ &=\bigcup_{r\in\delta(q_G,1)}\hat{\delta}(r,\upeps)\\ &=\hat{\delta}(q_G,\upeps)\\ &=\{q_G\} \end{align*}

DEFINIÇÃO 2.15. Dizemos que um AFN ou AFN-ε \(N=(Q, \Sigma,\delta,q_0, F)\) aceita uma palavra \(x\in \Sigma^{\ast}\) se \(\hat{\delta}(q_0,x)\cap F\neq\emptyset\), e que rejeita \(x\) se \(\hat{\delta}(q_0,x)\cap F=\emptyset\). Ainda, dizemos que o autômato aceita, ou reconhece, uma linguagem \(L\) sobre \(\Sigma\) se, para todo \(x\in \Sigma^{\ast}\), vale que \(N\) aceita \(x\) se e somente se \(x\in L\).

A linguagem que um AFN ou AFN-ε \(N\) aceita é chamada de a linguagem de \(N\) e denotada por \(L(N)\). Para o AFN \(N\) do nosso exemplo, temos \(L(N)=\{w01\mathbin{:}w\in\{0,1\}^{\ast}\}\). Para o AFN-ε \(E\) do nosso exemplo, \(L(E)\) é a linguagem dos números racionais com codificação finita em binário no sistema de representação de ponto fixo, com sinal e sem zeros à esquerda, permitindo-se a omissão do sinal quando o número representado é não-negativo, e permitindo-se a omissão do zero à esquerda do ponto separador decimal quando o valor absoluto do número representado é menor que 1.

• Base: [HMU06] Sec. 2.3.5, 2.5.5, 3.2, 4.1
• Exercícios: 9–16

LEMA 3.1. Considere uma linguagem \(L\) sobre um alfabeto \(\Sigma\). As seguintes afirmações são equivalentes a respeito de \(L\).

1. Existe um AFD cuja linguagem é \(L\).
2. Existe um AFN cuja linguagem é \(L\).
3. Existe um AFN-ε cuja linguagem é \(L\).

Demonstração. Seja \(\Sigma\) um alfabeto. Primeiro observemos que todo AFD \(A=(Q,\Sigma,\delta,q_0,F)\) pode ser imediatamente transformado em um AFN \(N=(Q,\Sigma,\delta',q_0,F)\) com \(L(N)=L(A)\) fazendo-se simplesmente \(\delta'(q,s)\bydef\{\delta(q,s)\}\) para todo \(q\in Q\) e todo \(s\in\Sigma\). Ainda, podemos imediatemente transformar qualquer AFN \(N=(Q,\Sigma,\delta',q_0,F)\) em um AFN-ε adicionando à função de transição \(\delta'\) as transições \(\delta'(q,\upeps)\bydef \emptyset\) para todo \(q\in Q\). Portanto, resta apenas mostrarmos que, para todo AFN-ε \(N\), existe um AFD \(A\) tal que \(L(A)=L(N)\).

Seja, então, \(N=(Q, \Sigma,\delta,q_0, F)\) um AFN-ε, e construamos o AFD \(A=(P,\Sigma,\zeta,S_0,G)\) definido por:

\begin{align*} P&=\Bigl\{S\subseteq Q\mathbin : \bigcup_{p\in S}\eclose(p)=S\Bigr\}\\ S_0&=\eclose(q_0)\,;\\ G&=\{S\in P \mathbin : S\cap F\neq\emptyset\}\,;\\ \zeta(S,a)&= \bigcup_{p\in S} \bigcup_{r\in \delta(p,a)}\eclose(r) \,,\quad\forall S\in P,\forall a\in\Sigma\,. \end{align*}

Vamos primeiramente mostrar, para todo \(x\in\Sigma^{\ast}\), que \(\hat{\zeta}(S,x)=\bigcup_{p\in S}\hat{\delta}(p,x)\) para todo \(S\in P\). Se \(x=\upeps\), temos

\begin{align*} \hat{\zeta}(S,\upeps)&= S\\ &= \bigcup_{p\in S}\eclose(p)\\ &= \bigcup_{p\in S}\hat{\delta}(p,\upeps)\,, \end{align*}

como queríamos. Suponhamos, então, que \(x=sw\), para algum \(s\in\Sigma\) e algum \(w\in\Sigma^{\ast}\). Suponhamos também, por indução, que, para todo \(y\in\Sigma^{\ast}\) com \(\lvert y\rvert < \lvert x\rvert\), vale que \(\hat{\zeta}(R,y)=\bigcup_{p\in R}\hat{\delta}(p,y)\) para todo \(R\in P\), notando que \(\bigcup_{p\in R}\hat{\delta}(p,y)=\bigcup_{p\in R}\eclose(\hat{\delta}(p,y))\) da Definição 2.14. Assim,

\begin{align*} \hat{\zeta}(S,x) &=\hat{\zeta}(\zeta(S,s),w)\\ &= \hat{\zeta}\biggl(\bigcup_{p\in S} \bigcup_{r\in \delta(p,s)}\eclose(r),w\biggr)\,. \end{align*}

Logo, como \(\bigcup_{p\in S}\bigcup_{r\in \delta(p,s)}\eclose(r)\in P\) e \(\lvert w\rvert < \lvert x\rvert\), temos, aplicando a hipótese da indução, que

\begin{align*} \hat{\zeta}(S,x) &=\bigcup_{q\in \bigcup_{p\in S}\bigcup_{r\in \delta(p,s)}\eclose(r)} \eclose(\hat{\delta}(q,w))\\ &=\bigcup_{p\in S} \bigcup_{r\in \delta(p,s)}\bigcup_{q\in\eclose(r)}\eclose(\hat{\delta}(q,w))\\ &=\bigcup_{p\in S}\eclose(\hat{\delta}(p,sw))\\ &=\bigcup_{p\in S}\hat{\delta}(p,sw)\,, \end{align*}

pela Definição 2.14.

Para concluirmos a demonstração, vamos mostrar que \(L(N)=L(A)\). Seja \(x\in\Sigma^{\ast}\). Sabemos que

\begin{equation*} \hat{\delta}(q_0,x)=\bigcup_{p\in S_0}\hat{\delta}(p,x) = \hat{\zeta}(S_0,x)\,. \end{equation*}

Assim, se \(\hat{\delta}(q_0,x)\cap F\neq\emptyset\), então \(\hat{\delta}(q_0,x)\in G\), o que implica \(L(N)\subseteq L(A)\). Por outro lado, se \(\hat{\delta}(q_0,x)\cap F=\emptyset\), então \(\hat{\delta}(q_0,x)\notin G\), o que contrapositivamente implica \(L(A)\subseteq L(N)\). □

DEFINIÇÃO 3.2. Sejam \(A=(Q, \Sigma,\delta,q_0, F)\) um AFD e \(n\) um inteiro positivo. Um passeio em \(A\) é uma sequência \(p_1s_1p_2s_2\dotsb s_{n-1}p_n\) tal que:

1. \(p_i\in Q\) para \(1\leq i\leq n\);
2. \(s_i\in \Sigma\) para \(1\leq i < n\);
3. \(\delta(p_i,s_i)=p_{i+1}\) para \(1\leq i < n\).

Ainda, dizemos que:

1. a palavra \(s_1s_2\dotsb s_{n-1}\in\Sigma^{n-1}\) é o rótulo do passeio \(p_1s_1p_2s_2\dotsb s_{n-1}p_n\), o que implica que se \(n=1\), então o rótulo do passeio é \(\upeps\);
2. \(p_1\) é a origem do passeio;
3. \(p_n\) é o destino do passeio;
4. \(p_2,\dotsc,p_{n-1}\) são os nós intermediários do passeio;
5. um passeio com origem \(p_1\) e destino \(p_n\) é um passeio de \(p_1\) até \(p_n\).

LEMA 3.3. Para todo AFD \(A\), existe uma expressão regular \(\varphi\) tal que \(L(\varphi)=L(A)\).

Demonstração. Seja \(A= (Q, \Sigma,\delta,q_0, F)\) um AFD, sejam \(n\bydef \lvert Q\rvert\) e \(m\bydef \lvert F\rvert\), e suponhamos sem perda de generalidade que \(Q=\{1,2,\dotsc,n\}\), sendo \(q_0=1\) e \(F=\{2,\dotsc,m+1\}\). Vamos construir, para quaisquer \(i,j\in Q\) e \(k\in\bN\), uma expressão regular denotada por \(\varphi_{ij}^{(k)}\) cuja linguagem seja a dos rótulos de todos os passeios de \(i\) até \(j\) que não possuem nó intermediário algum maior que \(k\). Deste modo, teremos que a expressão regular

\begin{equation*} \varphi\bydef \varphi_{1,2}^{(n)}\mathbin{\boldsymbol+} \varphi_{1,3}^{(n)}\mathbin{\boldsymbol+}\dotsb\mathbin{\boldsymbol+} \varphi_{1,m+1}^{(n)} \end{equation*}

satisfará \(L(\varphi)=L(A)\), uma vez que uma palavra \(w\) está em \(L(A)\) se e somente se existe um passeio com rótulo \(w\) de \(1\) até algum estado final (i.e. algum dentre os estados \(2,3,\dotsc,m+1\)), cujos nós intermediários certamente não são maiores que \(n\).

Sejam \(i,j\in Q\) e \(k\in\bN\). Se \(k=0\), é evidente que podemos fazer:

• se não há transição de \(i\) para \(j\) em \(A\),

  \begin{equation*} \varphi_{ij}^{(0)}\bydef \left\{ \begin{aligned} &\boldsymbol{\emptyset}\,,&&\text{se $i\neq j$,}\\ &\bupeps\,,&&\text{se $i= j$;} \end{aligned} \right. \end{equation*}

• se há transição de \(i\) para \(j\) em \(A\), sendo \(\{s\in \Sigma\mathbin : \delta(i,s)=j\} = \{a_1,a_2,\dotsc,a_t\}\),

  \begin{equation*} \varphi_{ij}^{(0)}\bydef \left\{ \begin{aligned} &\boldsymbol{a_1+a_2+\dotsb+a_t}\,,&&\text{se $i\neq j$,}\\ &\boldsymbol{a_1+a_2+\dotsb+a_t+\bupeps}\,,&&\text{se $i= j$.} \end{aligned} \right. \end{equation*}

Suponhamos, então, que \(k>0\) e, por indução em \(k\), que, para todo \(k' < k\), existe uma expressão regular \(\varphi_{ij}^{k'}\) cuja linguagem seja a dos rótulos de todos os passeios de \(i\) até \(j\) que não possuem nós intermediários maiores que \(k'\). Agora, consideremos um passeio de \(i\) até \(j\) que não possui nós intermediários maiores que \(k\). Temos duas possibilidades:

1. este passeio não possui \(k\) como nó intermediário e, portanto, seu rótulo é uma palavra da linguagem de \(\varphi_{ij}^{(k-1)}\), expressão regular esta que existe pela hipótese da indução;

2. este passeio possui ao menos uma ocorrência de \(k\) como nó intermediário e, portanto, seu rótulo é a concatenação de

   • uma palavra da linguagem de \(\varphi_{ik}^{(k-1)}\) com
   • zero ou mais palavras da linguagem de \(\varphi_{kk}^{(k-1)}\) com
   • uma palavra da linguagem de \(\varphi_{kj}^{(k-1)}\),

   garantida a existência das expressões \(\varphi_{ik}^{(k-1)}\), \(\varphi_{kk}^{(k-1)}\), e \(\varphi_{kj}^{(k-1)}\) pela hipótese da indução.

Logo, podemos fazer

\begin{equation*} \varphi_{ij}^{(k)}\bydef \varphi_{ij}^{(k-1)}\mathbin{\boldsymbol+} \varphi_{ik}^{(k-1)}\bigl(\varphi_{kk}^{(k-1)}\bigr)^{\boldsymbol{\ast}} \varphi_{kj}^{(k-1)}\,, \end{equation*}

o que conclui a demonstração. □

LEMA 3.4. Para toda expressão regular \(\varphi\), existe um AFN-ε \(N\) tal que \(L(N)=L(\varphi)\).

Demonstração. Vamos mostrar uma asserção ainda mais forte: que, para toda expressão regular \(\varphi\), existe um AFN-ε \(N\) com exatamente um estado final tal que \(L(N)=L(\varphi)\).

Seja \(\Sigma\) um alfabeto e seja \(\varphi\) uma expressão regular sobre \(\Sigma\). Se \(\varphi=\boldsymbol{\emptyset}\) ou se \(\varphi=\bupeps\), então \(L(\varphi)\) é a linguagem do autômato a seguir à esquerda ou à direita, respectivamente.

Se \(\varphi=\boldsymbol s\) para algum \(s\in\Sigma\), então \(L(\varphi)\) é a linguagem do autômato a seguir.

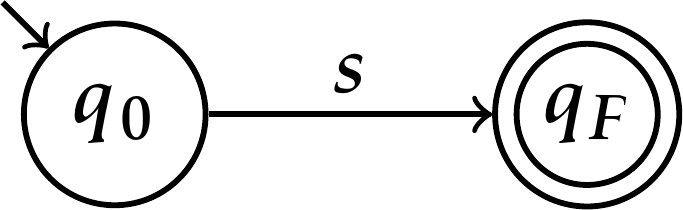
Suponhamos, então, que \(\varphi\) não é nenhuma das expressões regulares anteriores e, por indução, que para qualquer expressão regular \(\psi\) com \(\lvert \psi\rvert < \lvert\varphi\rvert\) existe um AFN-ε \(N_{\psi}\) tal que \(L(N_{\psi})=L(\psi)\). Temos os seguintes casos:

• \(\varphi=\varphi_1\mathbin{\boldsymbol+}\varphi_2\), sendo \(\varphi_1\) e \(\varphi_2\) duas expressões regulares sobre \(\Sigma\), com autômatos \(N_{\varphi_1}\) e \(N_{\varphi_2}\) pela hipótese da indução satisfazendo \(L(N_{\varphi_1})=L(\varphi_1)\) e \(L(N_{\varphi_2})=L(\varphi_2)\). Sendo \(p_0\) e \(p_F\) os estados inicial e final do autômato \(N_{\varphi_1}\), respectivamente, e \(r_0\) e \(r_F\) os estados inicial e final do autômato \(N_{\varphi_2}\), respectivamente, podemos construir o autômato \(N\) esquematizado a seguir.

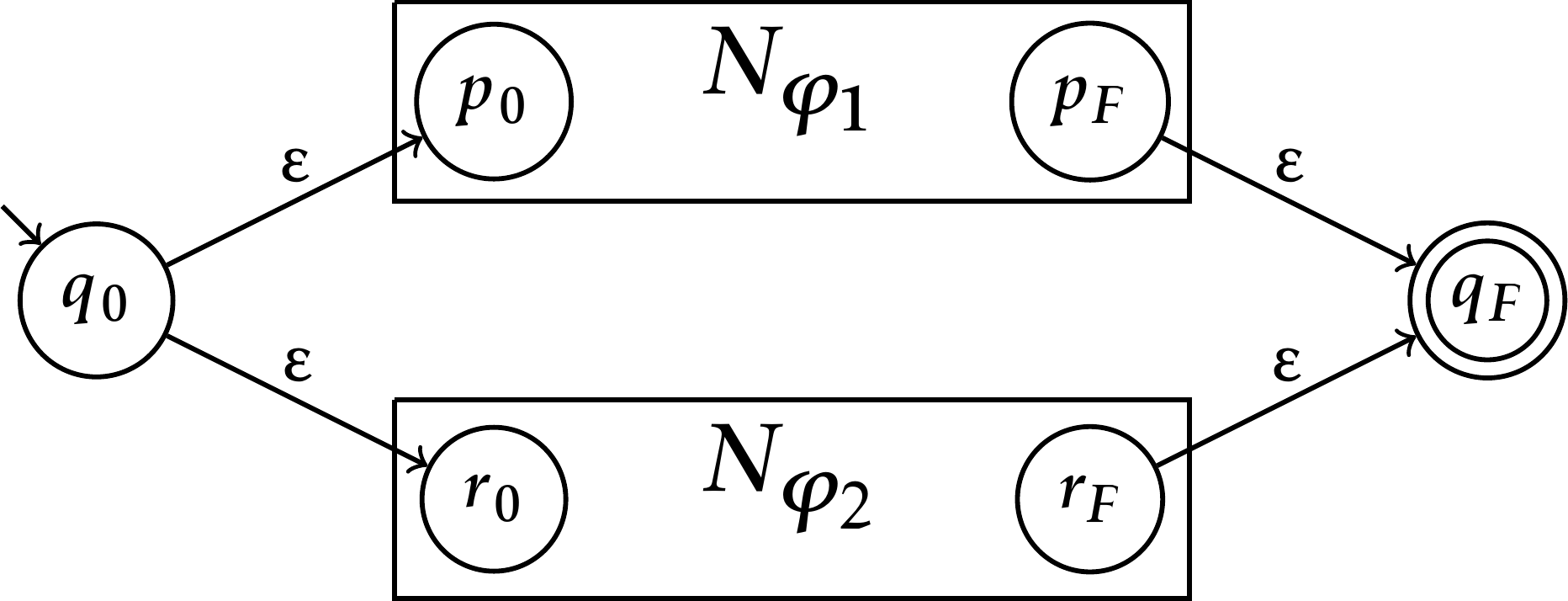
• \(\varphi=\varphi_1\varphi_2\), sendo \(\varphi_1\) e \(\varphi_2\) duas expressões regulares sobre \(\Sigma\), com autômatos \(N_{\varphi_1}\) e \(N_{\varphi_2}\) pela hipótese da indução satisfazendo satisfazendo \(L(N_{\varphi_1})=L(\varphi_1)\) e \(L(N_{\varphi_2})=L(\varphi_2)\).. Sendo \(p_0\) e \(p_F\) os estados inicial e final do autômato \(N_{\varphi_1}\), respectivamente, e \(r_0\) e \(r_F\) os estados inicial e final do autômato \(N_{\varphi_2}\), respectivamente, podemos construir o autômato \(N\) esquematizado a seguir.

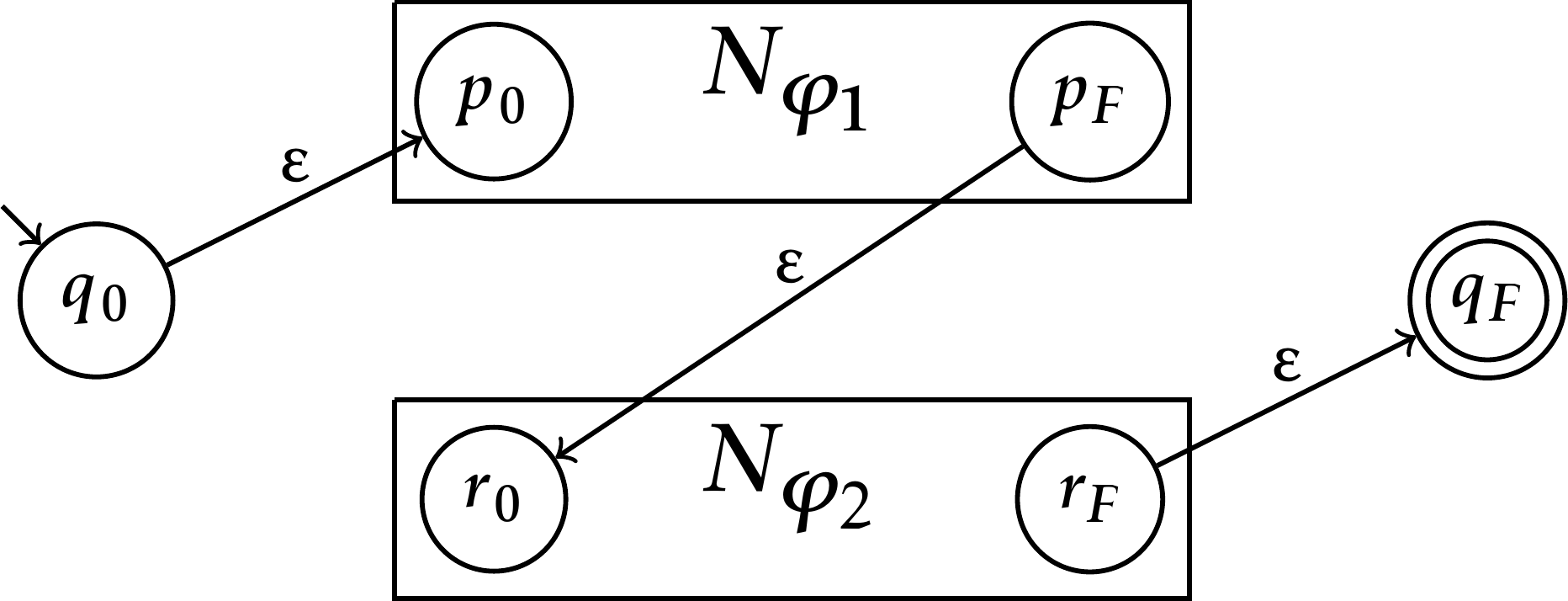
• \(\varphi=\varphi_1^{\boldsymbol{\ast}}\), sendo \(\varphi_1\) uma expressão regular sobre \(\Sigma\), com autômato \(N_{\varphi_1}\) pela hipótese da indução satisfazendo \(L(N_{\varphi_1})=L(\varphi_1)\). Sendo \(p_0\) e \(p_F\) os estados inicial e final do autômato \(N_{\varphi_1}\), respectivamente, podemos construir o autômato \(N\) esquematizado a seguir.

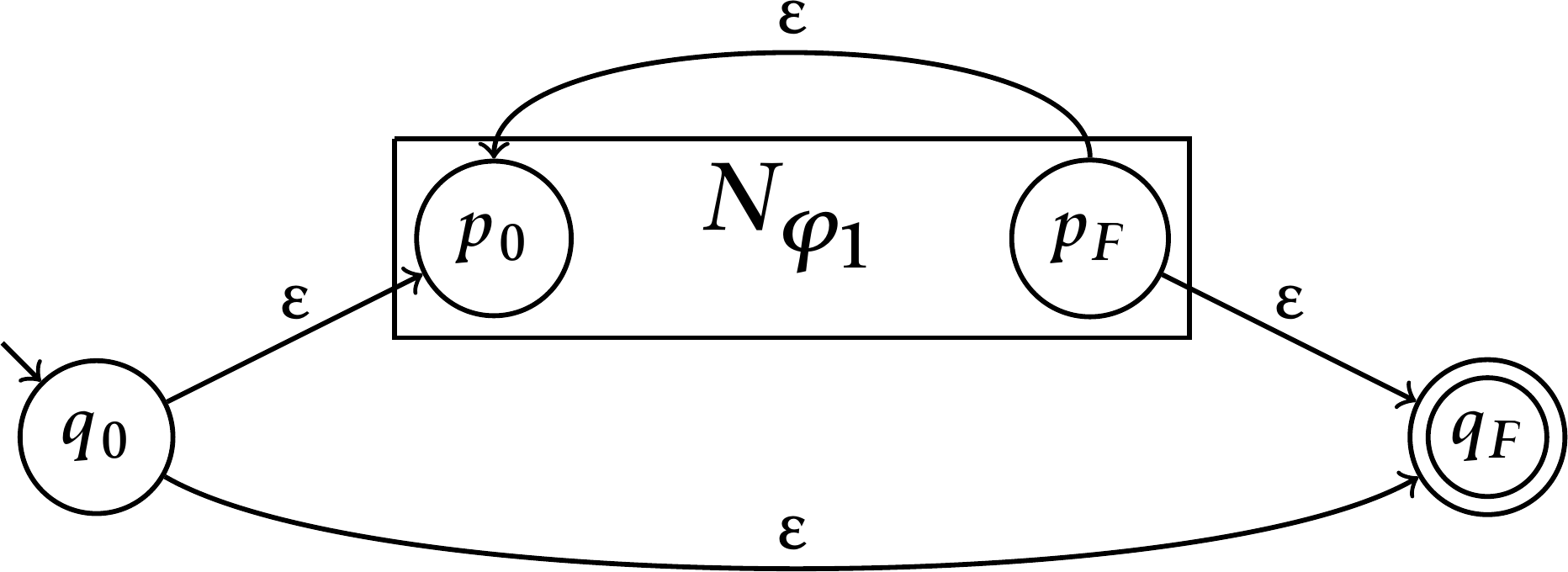
Em todos os casos, \(L(N)=L(\varphi)\). □

TEOREMA 3.5. Considere uma linguagem \(L\) sobre um alfabeto \(\Sigma\). As seguintes afirmações são equivalentes a respeito de \(L\).

1. \(L\) é regular.
2. Existe um AFD cuja linguagem é \(L\).
3. Existe um AFN cuja linguagem é \(L\).
4. Existe um AFN-ε cuja linguagem é \(L\). □

LEMA 3.6 (Lema de Bombeamento para linguagens regulares). Para toda linguagem regular \(L\) sobre um alfabeto \(\Sigma\), existe um inteiro \(n > 0\) tal que, para toda palavra \(w\) em \(L\) satisfazendo \(\lvert w\rvert\geq n\), existem \(x,y,z\in\Sigma^{\ast}\) tais que \(w=xyz\) e:

1. \(y\neq\upeps\);
2. \(\lvert xy\rvert\leq n\);
3. para todo inteiro \(k\geq 0\), a palavra \(xy^kz\) também está em \(L\).

Demonstração. Sejam \(L\) uma linguagem regular, \(A=(Q,\Sigma,\delta,q_0,F)\) um AFD que aceita \(L\), e \(n\bydef \lvert Q\rvert\). Se toda palavra em \(L\) tem comprimento menor que \(n\), o lema se verifica por vacuidade. Do contrário, seja \(w\bydef a_1a_2\dotsb a_m\) uma palavra em \(L\) tal que \(m\bydef \lvert w\rvert\geq n\). Ainda, seja, para \(0\leq i\leq m\), o estado \(p_i\bydef \hat{\delta}(q_0,a_1\dotsb a_i)\). Observe que, em particular, \(p_0=\hat{\delta}(q_0,\upeps)=q_0\). Observe também que \(p_m\in F\).

Como \(p_0,p_1,\dotsc,p_m\) é uma sequência de \(m+1 > n\) estados, temos, do Princípio da Casa dos Pombos, que existem inteiros \(i\) e \(j\) tais que \(0\leq i < j\leq n\) e \(p_i=p_j\). Sejam, então,

\begin{align*} x&=a_1\dotsb a_i\,,\\ y&=a_{i+1}\dotsb a_j\,,\\ z&=a_{j+1}\dotsb a_m\,. \end{align*}

Como \(i < j\leq n\), temos \(y\neq\upeps\) e \(\lvert xy\rvert \leq n\). Seja \(k\geq 0\) um inteiro. Como

\begin{equation*} p_i=\hat{\delta}(q_0,x)=\hat{\delta}(q_0,xy)=\hat{\delta}(q_0,xy^k)\,, \end{equation*}

temos

\begin{equation*} \hat{\delta}(q_0,xz)=\hat{\delta}(q_0,xyz)=\hat{\delta}(q_0,xy^kz)=p_m\in F\,. \end{equation*}

Portanto, \(xy^kz\in L\). □

TEOREMA 3.7. A linguagem \(L=\{0^n1^n \mathbin : n\in\bN\}\) não é regular.

Demonstração. Suponhamos que \(L\) seja regular. Tomemos, então, um inteiro positivo \(n\) tal como no enunciado do Lema de Bombeamento. Tomemos também \(w=0^n1^n\). Como \(\lvert w\rvert \geq n\), temos que existem \(x,y,z\in\Sigma^{\ast}\) tais que \(w=xyz\) satisfazendo as condições do lema. Em particular, \(xy^0z=xz\in L\). No entanto, como \(\lvert xy\rvert\leq n\), a palavra \(xy\) consiste somente em \(0\)s, e, como \(y\neq\upeps\), a palavra \(xz\) possui um número de \(0\)s menor que o de \(1\)s, o que nos traz, portanto, que \(xz\notin L\), uma contradição. □

• Base: [HMU06] Sec. 5.1–5.2, 6.1–6.3
• Exercicios: 17–23

DEFINIÇÃO 4.1. Uma gramática livre de contexto (GLC) é uma \(4\)-tupla \((V, \Sigma, {\to}, S)\) em que:

• \(V\) é o alfabeto das variáveis da gramática;
• \(\Sigma\) é o alfabeto dos terminais da gramática, necessariamente disjunto de \(V\);
• \({\to}\subseteq V\times (V\cup\Sigma)^{\ast}\) é o conjunto das produções da gramática, i.e. \(\to\) é uma relação binária de \(V\) em \((V\cup\Sigma)^{\ast}\), sendo que para cada relacionamento \((X,\alpha)\in\to\) chamamos \(X\) de cabeça da produção \(X\to \alpha\), assim como \(\alpha\) chamamos de corpo;
• \(S\in V\) é o símbolo inicial da gramática.

Como exemplo, considere a gramática \((\{S\},\{0,1\},{\to},S)\) definida pelo seguinte conjunto de produções:

\begin{align*} S&\to \upeps\\ S&\to 0S1 \end{align*}

Podemos também usar o símbolo \(\mid\) para o agrupamento de produções \(X\to \alpha_1\), \(X\to \alpha_2\), \(\ldots\), \(X\to \alpha_n\) que compartilhem da mesma cabeça \(X\), escrevendo simplesmente \(X\to \alpha_1\mid \alpha_2\mid\dotsb \mid \alpha_n\). No exemplo:

\begin{equation*} S\to\upeps \mid 0S1 \end{equation*}

DEFINIÇÃO 4.2. Sendo \(\Gamma=(V, \Sigma, {\to}, S)\) uma GLC, sendo \(X\to \gamma\) uma produção de \(\Gamma\), e sendo \(\alpha,\beta\in(V\cup\Sigma)^{\ast}\), escrevemos \(\alpha X\beta\underset{\Gamma}\Rightarrow \alpha\gamma\beta\), ou simplesmente \(\alpha X\beta\Rightarrow \alpha\gamma\beta\) quando livre de ambiguidade, para denotar a derivação de \(\alpha X\beta\) em \(\alpha\gamma\beta\) por \(\Gamma\). Sendo \(n\) um inteiro não-negativo e \(\alpha_1,\alpha_2\in(V\cup\Sigma)^{\ast}\), escrevemos \(\alpha_1\underset{\Gamma}{\overset{n}\Rightarrow} \alpha_2\), ou simplesmente \(\alpha_1\overset n \Rightarrow \alpha_2\), se \(\alpha_1=\alpha_2\) e \(n=0\), ou se \(n > 0\) e existe algum \(\alpha_3\in(V\cup\Sigma)^{\ast}\) tal que \(\alpha_1\underset{\Gamma}\Rightarrow \alpha_3\) e \(\alpha_3\underset{\Gamma}{\overset{n-1}\Rightarrow} \alpha_2\). Ainda, escrevemos \(\alpha_1\underset{\Gamma}{\overset{\ast}\Rightarrow} \alpha_2\) se existe algum inteiro não-negativo \(n\) tal que \(\alpha_1\underset{\Gamma}{\overset{n}\Rightarrow} \alpha_2\).

DEFINIÇÃO 4.3. Dizemos que uma palavra \(w\in \Sigma^{\ast}\) pode ser derivada por uma GLC \(\Gamma=(V, \Sigma, {\to}, S)\) se \(S\underset{\Gamma}{\overset{\ast}\Rightarrow} w\). A linguagem de \(\Gamma\), denotada por \(L(\Gamma)\), é o conjunto de todas as palavras sobre \(\Sigma\) que podem ser derivadas por \(\Gamma\).

Por exemplo, a linguagem da gramática \((\{S\},\{0,1\},{\to},S)\) definida pelo conjunto de produções \(S\to \upeps \mid 0S1\) é a linguagem \(\{0^n1^n\mathbin : n\in\bN\}\).

Nem sempre é imediato ver que uma determinada linguagem \(L\) é a linguagem de uma gramática \(\Gamma\). Às vezes, precisamos provar que \(L(\Gamma)=L\) por indução, como fazemos no Teorema 4.4.

TEOREMA 4.4. A linguagem da gramática \(\Gamma=(\{S\},\{0,1\},{\to},S)\) definida por

\begin{align*} S&\to\upeps\\ S&\to SS\\ S&\to 0S1\mid 1S0 \end{align*}

é a linguagem \(L=\{w\in\{0,1\}^{\ast}\mathbin: \#0(w)=\#1(w)\}\).

Demonstração. Vamos primeiro mostrar que \(L\subseteq L(\Gamma)\), i.e. que toda palavra \(w\in L\) pode ser derivada por \(\Gamma\). Sejam \(w\in L\) e \(n\bydef\lvert w\rvert\). Sabemos da definição de \(L\) que \(n\) é par. Se \(n=0\), temos que \(w=\upeps\) e que \(S\Rightarrow \upeps\) da definição de \(\Gamma\). Suponhamos, então, que \(n\geq 2\) e, por indução em \(n\), que \(S\overset{\ast}\Rightarrow w'\), para todo \(w'\in L\), tal que \(\lvert w'\rvert < n\). Vamos provar que \(S\overset{\ast}\Rightarrow w\).

Sendo \(w\bydef s_1s_2\dotsb s_{n}\) para \(s_1,s_2,\dotsc,s_n\in\Sigma\), se \(s_1\neq s_n\), então \(w=s_1 u s_n\) para algum \(u\in \Sigma^{\ast}\) tal que \(\#0(u)=\#1(u)\). Assim, \(u\in L\) e \(\lvert u\rvert < n\). Portanto, da hipótese da indução, temos que \(S\overset{\ast}\Rightarrow u\) e, de acordo com as produções \(S\to 0S1\mid 1S0\), que \(S\Rightarrow s_1Ss_n \overset{\ast}\Rightarrow s_1us_n=w\).

Vamos agora considerar o caso em que \(s_1=s_n\). Sendo \(s\bydef s_1=s_n\), seja \(r\) o outro valor em \(\{0,1\}\). Definamos \(w_i\bydef s_1s_2\dotsb s_i\) para \(1\leq i\leq n\). Definamos também \(d(i)\bydef \#s(w_i)-\#r(w_i)\). Ora, perceba-se que \(\lvert d(i)-d(i+1)\rvert=1\) para \(1\leq i < n\) e que \(d(1)=1\). Como \(d(n)=0\) porque \(w\in L\), temos que \(d(n-1)=-1\), já que \(s_n=s\). Então, existe necessariamente algum \(j\) tal que \(2\leq j\leq n-2\) e \(d(j)=0\). Logo, sendo \(u=w_j\) e \(v=s_{j+1}\dotsb s_{n}\), temos que \(u\) é uma palavra de \(L\) e, portanto, que \(v\) também o é, tendo ambas \(u\) e \(v\) comprimento menor que \(n\). Assim, da hipótese da indução, temos tanto que \(S\overset{\ast}\Rightarrow u\) quanto que \(S\overset{\ast}\Rightarrow v\), o que nos traz pela produção \(S\to SS\), que \(S\Rightarrow SS\overset{\ast}\Rightarrow uv=w\), como queríamos.

Para concluir a demonstração, precisamos ainda mostrar que \(L(\Gamma)\subseteq L\), i.e. que toda palavra de \(\{0,1\}^{\ast}\) que podemos derivar por \(\Gamma\) possui igual número de \(0\)s e \(1\)s. Vamos mostrar uma asserção ainda mais forte: vamos mostrar que para toda palavra \(\alpha\in \{0,1,S\}^{\ast}\) tal que \(S\overset{n}\Rightarrow \alpha\) para algum inteiro não-negativo \(n\), vale que \(\#0(\alpha)=\#1(\alpha)\), ainda que \(\alpha\) contenha símbolos não-terminais (variáveis). Ora, se \(n=0\), então \(\alpha=S\); logo, \(\#0(\alpha)=\#1(\alpha)=0\). Suponhamos, então, que \(n > 0\) e, por indução em \(n\), que para todo \(\alpha'\) tal que \(S\overset{n'}\Rightarrow\alpha'\), para \(n' < n\), valha que \(\#0(\alpha')=\#1(\alpha')\). Deste modo, sendo \(\beta\in\{0,1,S\}^{\ast}\) tal que \(S\overset{n-1}\Rightarrow\beta\Rightarrow\alpha\), vale da hipótese da indução que \(\#0(\beta)=\#1(\beta)\). Temos os seguintes casos:

1. se \(\beta\Rightarrow\alpha\) pela produção \(S\to \upeps\) ou pela produção \(S\to SS\), então \(\#0(\alpha)=\#0(\beta)=\#1(\beta)=\#1(\alpha)\), como queríamos;
2. por outro lado, se \(\beta\Rightarrow\alpha\) pela produção \(S\to 0S1\) ou pela produção \(S\to 1S0\), então \(\#0(\alpha)=1+\#0(\beta)=1+\#1(\beta)=\#1(\alpha)\), também como queríamos. □

Um caso particular de gramática livre de contexto é uma gramática regular, conforme definimos a seguir.

DEFINIÇÃO 4.5. Uma gramática livre de contexto \(\Gamma=(V, \Sigma, {\to}, S)\) é dita regular à direita se toda produção de \(\Gamma\) é de uma das seguintes formas:

1. \(X\to\upeps\) para algum \(X\in V\);
2. \(X\to s\) para algum \(X\in V\) e algum \(s\in\Sigma\);
3. \(X\to sY\) para \(X,Y\in V\) (não necessariamente distintos) e \(s\in\Sigma\).

DEFINIÇÃO 4.6. Uma gramática livre de contexto \(\Gamma=(V, \Sigma, {\to}, S)\) é dita regular à esquerda se toda produção de \(\Gamma\) é de uma das seguintes formas:

1. \(X\to\upeps\) para algum \(X\in V\);
2. \(X\to s\) para algum \(X\in V\) e algum \(s\in\Sigma\);
3. \(X\to Ys\) para \(X,Y\in V\) (não necessariamente distintos) e \(s\in\Sigma\).

DEFINIÇÃO 4.7. Uma gramática livre de contexto \(\Gamma=(V, \Sigma, {\to}, S)\) é dita regular se ou é regular à esquerda, ou é regular à direita.

Observe que a gramática \((\{S\},\{0,1\},{\to}, S)\) definida por \(S\to\upeps\mid 0S\mid S1\) não é regular, pois não é regular à esquerda, nem regular à direita.

Uma linguagem é regular se e somente se é a linguagem de uma gramática regular (cf. Exercício 3). Assim, toda linguagem regular é uma linguagem livre de contexto, embora nem toda linguagem livre de contexto seja regular. Por outro lado, uma gramática livre de contexto é um caso particular de uma gramática sensível ao contexto. Gramáticas sensíveis ao contexto, por sua vez, são casos particulares de gramáticas irrestritas, cujas linguagens são chamadas de linguagens recursivamente enumeráveis, conforme ficará claro nas próximas aulas. Assim, temos uma hierarquia de classes de linguagens, conhecida como a Hierarquia de Chomsky, de quatro níveis, especificados a seguir, em que a classe das linguagens de cada nível inclui as linguagens do nível seguinte.

Nível	Linguagens	Gramáticas
0	Linguagens recursivamente enumeráveis	Gramáticas irrestritas
1	Linguagens sensíveis ao contexto	Gramáticas sensíveis ao contexto
2	Linguagens livres de contexto	Gramáticas livres de contexto
3	Linguagens regulares	Gramáticas regulares

DEFINIÇÃO 4.8. Um autômato finito não-determinístico com transições-ε e pilha, ou simplesmente autômato com pilha (AP), é uma \(7\)-tupla \((Q,\Sigma,Z,\delta,q_0,z_0,F)\) em que:

• \(Q\) é o conjunto de estados do autômato, um conjunto finito e não-vazio;
• \(\Sigma\) é o alfabeto do autômato, satisfazendo \(\upeps\notin\Sigma\);
• \(Z\) é o alfabeto da pilha do autômato (não necessariamente disjunto de \(\Sigma\));
• \(\delta\colon Q\times(\Sigma\cup\{\upeps\})\times Z\to 2^{Q\times (Z^{\ast})}\) é a função de transição do autômato;
• \(q_0\in Q\) é o estado inicial do autômato;
• \(z_0\in Z\) é o símbolo inicial da pilha do autômato;
• \(F\subseteq Q\) é o conjunto de estados finais do autômato.

Como exemplo apresentamos \(A=(\{q_0,q_1,q_F\},\{0,1\},\{z_0,0,1\},\delta,q_0,z_0,\{q_F\})\), sendo \(\delta\) a função de transição definida pela tabela a seguir, convencionando-se que transições omitidas correspondem a transições vazias (i.e. se uma tripla \((q,s,z)\in Q\times(\Sigma\cup\{\upeps\})\times Z\) não consta na tabela, então convencionamos que \(\delta(q,s,z)=\emptyset\)).

\((q,s,z)\)	\(\delta(q,s,z)\)
\((q_0, 0,z_0)\)	\(\{(q_0,0z_0)\}\)
\((q_0, 1,z_0)\)	\(\{(q_0,1z_0)\}\)
\((q_0, 0,0)\)	\(\{(q_0,00)\}\)
\((q_0, 0,1)\)	\(\{(q_0,01)\}\)
\((q_0, 1,0)\)	\(\{(q_0,10)\}\)
\((q_0, 1,1)\)	\(\{(q_0,11)\}\)
\((q_0, \upeps,z_0)\)	\(\{(q_1,z_0)\}\)
\((q_0, \upeps,0)\)	\(\{(q_1,0)\}\)
\((q_0, \upeps,1)\)	\(\{(q_1,1)\}\)
\((q_1, 0,0)\)	\(\{(q_1,\upeps)\}\)
\((q_1, 1,1)\)	\(\{(q_1,\upeps)\}\)
\((q_1, \upeps,z_0)\)	\(\{(q_F,z_0)\}\)

DEFINIÇÃO 4.9. O diagrama de transições de um AP \(A=(Q,\Sigma,Z,\delta,q_0,z_0,F)\) é a representação de um grafo dirigido cujos vértices são os estados de \(A\) e, para cada \((q,s,z)\in Q\times(\Sigma\cup\{\upeps\})\times Z\) e cada \((p,\alpha)\in\delta(q,s,z)\), há um arco de \(q\) para \(p\) rotulado com \(s,z/\alpha\). O estado \(q_0\) é identificado por um semiarco chegando no vértice correspondente, assim como cada estado final é identificado circulando-se duplamente o vértice correspondente. Arcos paralelos com diferentes rótulos podem ser representados por um único arco separando-se os rótulos por quebra de linha.

O autômato \(A\) do nosso exemplo é o autômato representado pelo diagrama de transições a seguir.

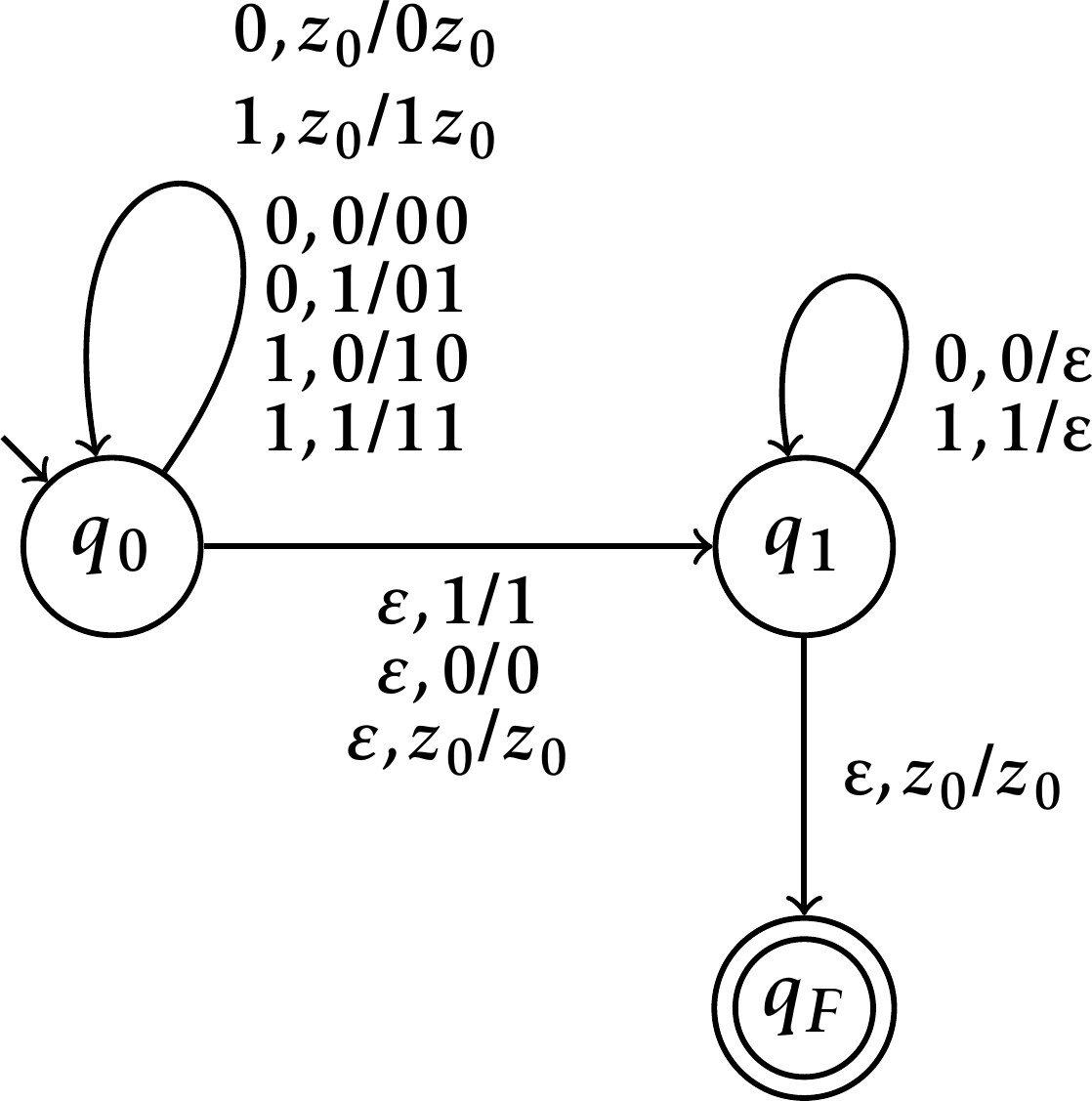
DEFINIÇÃO 4.10. Uma configuração (ou descrição instantânea) de um AP \((Q,\Sigma,Z,\delta,q_0,z_0,F)\) é uma tripla \((q,w,\alpha)\) em que:

• \(q\in Q\) é o estado em que se encontra o processamento da palavra de entrada;
• \(w\in\Sigma^{\ast}\) é o sufixo da palavra de entrada que ainda resta a ser processado;
• \(\alpha\in Z^{\ast}\) é o conteúdo atual da pilha (sendo o primeiro símbolo de \(\alpha\) o símbolo no topo da pilha).

DEFINIÇÃO 4.11. Sendo \(A=(Q,\Sigma,Z,\delta,q_0,z_0,F)\) um AP, e sendo \(q,p\in Q\), \(s\in \Sigma\cup\{\upeps\}\), \(w\in\Sigma^{\ast}\), \(z\in Z\), e \(\alpha,\beta\in Z^{\ast}\), dizemos que a configuração \((q,sw,z\alpha)\) alcança a configuração \((p,w,\beta\alpha)\) por \(A\), e escrevemos \((q,sw,z\alpha)\underset{A}\Rightarrow (p,w,\beta\alpha)\), ou simplesmente \((q,sw,z\alpha)\Rightarrow (p,w,\beta\alpha)\) quando livre de ambiguidade, se \((p,\beta)\in\delta(q,s,z)\). Sendo \(n\) um inteiro não-negativo e \(C_1\) e \(C_2\) duas configurações de \(A\), escrevemos \(C_1\underset A{\overset n\Rightarrow} C_2\), ou simplesmente \(C_1\overset n\Rightarrow C_2\) quando livre de ambiguidade, se \(C_1=C_2\) e \(n=0\), ou se \(n > 0\) e existe alguma configuração \(C_3\) de \(A\) tal que \(C_1\underset A{\overset{n-1}\Rightarrow} C_3\) e \(C_3\underset A\Rightarrow C_2\). Ainda, escrevemos \(C_1\underset A{\overset{\ast}\Rightarrow} C_2\) se existe algum inteiro não-negativo \(n\) tal que \(C_1\underset A{\overset n\Rightarrow} C_2\).

DEFINIÇÃO 4.12. Dizemos que um AP \(A=(Q,\Sigma,Z,\delta,q_0,z_0,F)\) aceita por estado final, ou simplesmente aceita, uma palavra \(x\in\Sigma^{\ast}\) se \((q_0,x,z_0)\underset A{\overset{\ast}\Rightarrow} (p,\upeps,\alpha)\) para algum \(p\in F\) e algum \(\alpha\in Z^{\ast}\) qualquer. A linguagem de \(A\), denotada por \(L(A)\), é a linguagem que \(A\) aceita, ou reconhece, por estado final, i.e. a linguagem das palavras que \(A\) aceita por estado final.

Considerando o AP do nosso exemplo, podemos mostrar que o autômato aceita \(0110\), pois

\begin{align*} (q_0,0110,z_0)&\Rightarrow (q_0,110,0z_0)\\ &\Rightarrow (q_0,10,10z_0)\\ &\Rightarrow (q_1,10,10z_0)\\ &\Rightarrow (q_1,0,0z_0)\\ &\Rightarrow (q_1,\upeps,z_0)\\ &\Rightarrow (q_F,\upeps,z_0)\,. \end{align*}

Também podemos mostrar que a linguagem do autômato é a linguagem dos palíndromos binários de comprimento par (Exercício 19).

DEFINIÇÃO 4.13. Dizemos que um AP \(A=(Q,\Sigma,Z,\delta,q_0,z_0,F)\) aceita por pilha vazia uma palavra \(x\in\Sigma^{\ast}\) se \((q_0,x,z_0)\underset A{\overset{\ast}\Rightarrow} (p,\upeps,\upeps)\) para algum \(p\in Q\) (não necessariamente em \(F\)). A linguagem que \(A\) aceita, ou reconhece, por pilha vazia denotamos por \(N(A)\).

TEOREMA 4.14. Sendo \(L\) uma linguagem, existe um AP \(A\) tal que \(L(A)=L\) se e somente se existe um AP \(B\) tal que \(N(B)=L\).

Demonstração. (Suficiência) Seja \(A= (Q,\Sigma,Z,\delta,q_0,z_0,F)\) um AP tal que \(L(A)=L\). Construamos o AP \(B=(Q\cup\{p_0,p_1\},\Sigma,Z\cup\{x_0\},\delta',p_0,x_0,\emptyset)\), supondo \(p_0,p_1\notin Q\) e \(x_0\notin Z\), sendo \(\delta'\) a função de transição definida a partir de \(\delta\) com a adição das seguintes transições:

\begin{align*} \delta'(p_0,\upeps,x_0)&\;\bydef\; (q_0,z_0x_0)\,;\\ \delta'(q,\upeps,z)&\;\bydef\;(p_1,\upeps)\,,\quad\forall q\in F,\forall z\in Z\cup\{x_0\}\,;\\ \delta'(p_1,\upeps,z)&\;\bydef\;(p_1,\upeps)\,,\quad\forall z\in Z\cup\{x_0\}\,. \end{align*}

A fim de completude, para todo \((q,s,z)\in Q\times(\Sigma\cup\{\upeps\})\times Z\) para o qual \(\delta'\) não esteja definida, simplesmente definamos \(\delta'(q,s,z)\bydef \emptyset\).

Vamos mostrar que \(N(B)\subseteq L(A)\). Seja \(w\in N(B)\). Então, \((p_0,w,x_0)\underset B{\overset{\ast}\Rightarrow} (p_1,\upeps,\upeps)\), pois, uma vez que \(x_0\notin Z\), as únicas transições de \(B\) capazes de desempilhar o símbolo \(x_0\) são as transições-ε que movem dos estados em \(F\) para o estado \(p_1\). Logo, \((p_0,w,x_0)\underset B{\overset{\ast}\Rightarrow} (q,\upeps,\alpha x_0)\) para algum \(q\in F\) e algum \(\alpha\in (Z\cup\{x_0\})^{\ast}\), e, portanto, \((p_0,w,x_0)\underset B\Rightarrow (q_0,w,z_0x_0)\underset B{\overset{\ast}\Rightarrow}(q,\upeps,\alpha x_0)\), o que implica \((q_0,w,z_0)\underset A{\overset{\ast}\Rightarrow}(q,\upeps,\alpha)\) e, consequentemente, \(x\in L(A)\).

Resta mostrar que \(L(A)\subseteq N(B)\). Seja \(w\in L(A)\). Como \((q_0,w,z_0)\underset A{\overset{\ast}\Rightarrow}(q,\upeps,\alpha)\) para algum \(q\in F\) e algum \(\alpha\in (Z\cup\{x_0\})^{\ast}\), temos \((p_0,w,x_0)\underset B\Rightarrow (q_0,w,z_0x_0)\underset B{\overset{\ast}\Rightarrow}(q,\upeps,\alpha x_0)\underset B{\overset{\ast}\Rightarrow} (p_1,\upeps,\upeps)\), e, assim, \(x\in N(B)\).

(Necessidade) Seja \(B= (Q,\Sigma,Z,\delta,p_0,x_0,\emptyset)\) um AP tal que \(N(B)=L\). Construamos o AP \(A= (Q\cup\{q_0,q_F\},\Sigma,Z\cup\{z_0\},\delta',q_0,z_0,\{q_F\})\), supondo \(q_0,q_F\notin Q\) e \(z_0\notin Z\), sendo \(\delta'\) a função de transição definida a partir de \(\delta\) com a adição das seguintes transições:

\begin{align*} \delta'(q_0,\upeps,z_0)&\;\bydef\; (p_0,x_0z_0)\,;\\ \delta'(p,\upeps,z_0)&\;\bydef\; (q_F,z_0)\,,\forall p\in Q\,. \end{align*}

A fim de completude, para todo \((p,s,z)\in Q\times(\Sigma\cup\{\upeps\})\times Z\) para o qual \(\delta'\) não esteja definida, simplesmente definamos \(\delta'(p,s,z)\bydef \emptyset\).

Vamos mostrar que \(L(A)\subseteq N(B)\). Seja \(w\in L(A)\). Então, \((q_0,w,z_0)\underset A\Rightarrow(p_0,w,x_0z_0) \underset A{\overset{\ast}\Rightarrow} (p,\upeps,z_0)\underset A\Rightarrow (q_F,\upeps,z_0)\) para algum \(p\in Q\). Portanto, como \(z_0\notin Z\), temos \((p_0,w,x_0) \underset B{\overset{\ast}\Rightarrow} (p,\upeps,\upeps)\), e assim concluímos que \(w\in N(B)\).

Vamos agora mostrar que \(N(B)\subseteq L(A)\), concluindo a demonstração. Seja \(w\in N(B)\). Então, \((p_0,w,x_0) \underset B{\overset{\ast}\Rightarrow} (p,\upeps,\upeps)\) para algum \(p\in Q\), e, portanto, \((q_0,w,z_0)\underset A\Rightarrow(p_0,w,x_0z_0) \underset A{\overset{\ast}\Rightarrow} (p,\upeps,z_0)\underset A\Rightarrow (q_F,\upeps,z_0)\). Logo, \(w\in L(A)\). □

DEFINIÇÃO 4.15. Uma árvore de derivação por uma gramática livre de contexto \(\Gamma=(V, \Sigma, {\to}, S)\) é uma árvore enraizada \(T\) com nós rotulados por uma função de rotulação \(\ell\) satisfazendo as seguintes condições:

1. se \(u\) é um nó interno de \(T\), então \(\ell(u)\in V\);
2. se \(u\) é uma folha de \(T\), então \(\ell(u)\in V\cup\Sigma\cup\{\epsilon\}\);
3. se \(\ell(u)=\varepsilon\), então \(u\) é o único filho do pai de \(u\);
4. se \(u\) é um nó interno de \(T\), com \(\ell(u)=A\) para algum \(A\in V\), e se os rótulos dos seus filhos são, da esquerda para direita, \(X_1,X_2,\dotsc,X_k\), então \(A\to X_1X_2\dotsb X_k\) é uma produção de \(\Gamma\).

DEFINIÇÃO 4.16. Se \(T\) é uma árvore de derivação para uma GLC \(\Gamma=(V, \Sigma, {\to}, S)\) tal que o rótulo de nenhuma folha é uma variável, então \(T\) é dita completa, e a derivada de \(T\) é a palavra em \(\Sigma^{\ast}\) que se lê concatenando-se os rótulos das folhas de \(T\) da esquerda para direita.

TEOREMA 4.17. Considere uma linguagem \(L\) sobre um alfabeto \(\Sigma\). As seguintes afirmações são equivalentes a respeito de \(L\).

1. \(L\) é livre de contexto.
2. Existe um AP \(A\) tal que \(N(A)=L\).
3. Existe um AP \(B\) tal que \(L(B)=L\).

Demonstração. Tendo em vista o Teorema 4.14, vamos apenas mostrar que uma linguagem \(L\) é livre de contexto se e somente se existe um AP \(A\) tal que \(N(A)=L\).

(Suficiência) Seja \(L\) uma linguagem livre de contexto sobre um alfabeto \(\Sigma\) e seja \(\Gamma=(V, \Sigma, {\to}, S)\) tal que \(L(\Gamma)=L\). Vamos construir um AP \(A\) tal que \(N(A)=L\).

Seja \(A=(\{q_0\},\Sigma,\Sigma\cup V,\delta,q_0,S,\emptyset)\) tal que \(\delta\) é a função de transição definida por:

\begin{align*} \delta(q_0,\upeps,X) &\;\bydef\; \{(q_0,\alpha)\mathbin : \text{$X\to \alpha$ é uma produção de $\Gamma$}\}&&\forall X\in V\,;\\ \delta(q_0,s,s) &\;\bydef\; \{(q_0,\upeps)\}&&\forall s\in \Sigma\,. \end{align*}

Vamos mostrar que \(N(A)=L\), mostrando que \((q_0,w,S)\underset A{\overset{n}\Rightarrow}(q_0,y,\alpha)\) se e somente se \(S\underset{\Gamma}{\overset {\ast}\Rightarrow}x\alpha\), para \(n\in\bN\), \(\alpha\in(V\cup\Sigma)^{\ast}\), e \(w,x,y\in\Sigma^{\ast}\) tais que \(w=xy\). Observe que disto segue que \((q_0,w,S)\underset A{\overset{\ast}\Rightarrow}(q_0,\upeps,\upeps)\) se e somente se \(S\underset{\Gamma}{\overset \ast\Rightarrow}w\), o que nos traz que \(N(A)=L\), como queremos.

Se \(n=0\), temos imediatamente que \((q_0,w,S)\underset A{\overset{0}\Rightarrow}(q_0,y,\alpha)\) se e somente se \(S\underset{\Gamma}{\overset {\ast}\Rightarrow}x\alpha\), com \(x=\upeps\), \(y=w\), e \(\alpha=S\). Suponhamos, então, que \(n > 0\). Ora, se vale, por indução, que \((q_0,w,S)\underset A{\overset{n-1}\Rightarrow}(q_0,y',\alpha')\) se e somente se \(S\underset{\Gamma}{\overset {\ast}\Rightarrow}x'\alpha'\), com \(w=x'y'\), temos que \((q_0,w,S)\underset A{\overset{n-1}\Rightarrow}(q_0,y',\alpha')\underset A\Rightarrow(q_0,y,\alpha)\) se e somente se: ou \(y' = y\) e \(x' = x\), situação em que \(\alpha' = X\beta\) e \(\alpha=\gamma\beta\) para alguma produção \(X\to\gamma\) de \(\Gamma\) e algum \(\beta\in(V\cup\Sigma)^{\ast}\); ou \(y' = sy\) e \(x=sx'\) para algum \(s\in\Sigma\), situação em que \(\alpha'=s\alpha\). Em ambas as situações, \(x'\alpha'\underset{\Gamma}{\overset{\ast}\Rightarrow} x\alpha\), como queríamos.

(Necessidade) Seja \(A=(Q,\Sigma,Z,\delta,q_0,Z_0,F)\) um AP. Vamos construir uma GLC \(\Gamma\) tal que \(L(\Gamma)=N(A)\).

Seja \(\Gamma=(\{S\}\cup \{[pXq]\mathbin : p,q\in Q\text{ e }X\in Z\},\Sigma,{\to}\,S)\) a GLC cujas produções são todas as listadas a seguir:

• \(S\to [q_0Z_0p]\) para todo \(p\in Q\);
• \([qXr]\to a\), para quaisquer \(q\in Q,a\in\Sigma\cup\{\upeps\},X\in Z\) e qualquer, se algum, \((r,\upeps)\in\delta(q,a,X)\);
• \([qXr_k]\to a[rY_1r_1][r_1Y_2r_2]\dotsb[r_{k-1}Y_kr_k]\), para quaisquer \(q\in Q,a\in\Sigma\cup\{\upeps\},X\in Z\), qualquer \((r,Y_1Y_2\dotsb Y_k)\in\delta(q,a,X)\) com \(k\geq 1\), e qualquer tupla \((r_1,r_2,\dotsc,r_k)\) de \(k\) estados em \(Q\) não necessariamente distintos.

Perceba-se que as produções do segundo tipo listadas acima são casos particulares das produções do terceiro.

Vamos mostrar que \(L(\Gamma)=N(A)\), mostrando que \([qXp]\underset{\Gamma}{\overset{\ast}\Rightarrow} w\), para \(q,p\in Q\), \(X\in Z\), e \(w\in\Sigma^{\ast}\), se e somente se \((q,w,X)\underset{A}{\overset{n}\Rightarrow} (p,\upeps,\upeps)\) para algum \(n\in\bZ_{> 0}\). Observe que disto segue que \(S\underset{\Gamma}{\overset{\ast}\Rightarrow} w\), para \(w\in\Sigma^{\ast}\), se e somente se \((q_0,w,Z_0)\underset{A}{\overset{\ast}\Rightarrow} (p,\upeps,\upeps)\) para algum \(p\in Q\) (uma vez que as únicas produções que têm \(S\) como cabeça são da forma \(S\to [q_0Z_0p]\)), o que nos traz que \(L(\Gamma)=N(A)\), como queremos.

Se \(n=1\), temos \(w=s\) para algum \(s\in\Sigma\cup\{\upeps\}\), \(X=Z_0\), e \((p,\upeps)\in\delta(q,s,Z_0)\), e, por construção, \([qXp]\underset{\Gamma}\Rightarrow s\). Suponhamos, então, que \(n > 0\) e, por indução em \(n\), que \([q'X'p']\underset{\Gamma}{\overset{\ast}\Rightarrow} w'\) se e somente se \((q',w',X')\underset{A}{\overset{n'}\Rightarrow} (p',\upeps,\upeps)\), para \(q',p'\in Q\), \(X'\in Z\), \(w'\in\Sigma^{\ast}\), e todo inteiro positivo \(n' < n\). Assim, novamente por construção, sendo \((r,Y_1Y_2\dotsb Y_k)\in\delta(q,s,X)\) e \(w=sx\) para \(s\in\Sigma\cup\{\upeps\}\) e \(x\in\Sigma^{\ast}\),

\begin{equation*} (q,sx,X)\underset{A}\Rightarrow(r,x,Y_1Y_2\dotsb Y_k)\underset{A}{\overset{n-1}\Rightarrow} (p,\upeps,\upeps) \end{equation*}

se e somente se existem \(x_1,x_2,\dotsb,x_k\in\Sigma^{\ast}\) tais que \(x=x_1x_2\dotsb x_k\) e

\begin{align*} (r,x_1,Y_1)&\underset{A}{\overset{n_1}\Rightarrow} (r_1,\upeps,\upeps) &&\exists n_1 > 0,\exists r_1\in Q,\\ (r_1,x_2,Y_2)&\underset{A}{\overset{n_2}\Rightarrow} (r_2,\upeps,\upeps) &&\exists n_2 > 0,\exists r_2\in Q,\\ &\vdots\\ (r_{k-1},x_k,Y_k)&\underset{A}{\overset{n_k}\Rightarrow} (p,\upeps,\upeps) &&\exists n_k > 0, \end{align*}

o que, por construção e pela hipótese da indução, ocorre se e somente se

\begin{equation*} [qXp]\underset{\Gamma}\Rightarrow s[rY_1r_1][r_1Y_2r_2]\dotsb [r_{k-1}Y_k p]\underset{\Gamma}{\overset{\ast}\Rightarrow} sx_1x_2\dotsb x_k\,, \end{equation*}

como queríamos. □

• Base: [HMU06] Sec. 7.1–7.2
• Exercícios: 24–25

DEFINIÇÃO A.1. Uma gramática livre de contexto \(\Gamma=(V, \Sigma, {\to}, S)\) está na forma normal de Chomsky se toda produção de \(\Gamma\) é de uma das seguintes formas:

1. \(X\to s\) para algum \(X\in V\) e algum \(s\in\Sigma\);
2. \(X\to YZ\) para \(X,Y,Z\in V\).

TEOREMA A.2. Para toda GLC \(\Gamma\) tal que \(L(\Gamma)\setminus\{\upeps\}\neq\emptyset\), existe uma GLC \(\Gamma'\) na forma normal de Chomsky tal que \(L(\Gamma')=L(\Gamma)\setminus\{\upeps\}\). □

LEMA A.3 (Lema de Bombeamento para linguagens livres de contexto). Para toda linguagem livre de contexto \(L\) sobre um alfabeto \(\Sigma\), existe um inteiro \(n > 0\) tal que, para toda palavra \(w\) em \(L\) satisfazendo \(\lvert w\rvert\geq n\), existem \(u,v,x,y,z\in\Sigma^{\ast}\) tais que \(w=uvxyz\) e:

1. \(vy\neq\varepsilon\);
2. \(\lvert vxy\rvert\leq n\);
3. para todo inteiro \(k\geq 0\), a palavra \(uv^kxy^kz\) também está em \(L\).

Demonstração. Seja \(L\) uma linguagem livre de contexto sobre um alfabeto \(\Sigma\), seja \(\Gamma=(V,\Sigma,{\to},S)\) uma GLC na forma normal de Chomsky tal que \(L(\Gamma)=L\setminus\{\upeps\}\), e seja \(n\bydef 2^{\lvert V\rvert}\). Se toda palavra em \(L\) tem comprimento menor que \(n\), o lema se verifica por vacuidade. Do contrário, seja \(w\bydef a_1a_2\dotsb a_m\), com \(m\bydef \lvert w\rvert\geq n\), uma palavra de \(L\). Note-se que \(w\) também é uma palavra de \(L(\Gamma)\), uma vez que \(n > 0\). Seja, então, \(T\) uma árvore de derivação completa por \(\Gamma\) enraizada em \(S\) cuja derivada seja \(w\), e seja \(X_0,X_1,\dotsc,X_h\), para \(h > 0\), um caminho em \(T\) de comprimento máximo de \(X_0=S\) a alguma folha \(X_h\). Observe que \(X_0,X_1,\dotsc,X_{h-1}\) é uma sequência de \(h\) variáveis de \(\Gamma\), e que \(X_h\) é um terminal de \(\Gamma\).

Como \(m\geq 2^{\lvert V\rvert}\), temos que \(h\geq \lvert V\rvert + 1\). Portanto, do Princípio da Casa dos Pombos, existem inteiros \(i\) e \(j\) tais que \(h - \lvert V\rvert - 1\leq i < j < h\) e \(X_i=X_j\). Sejam \(w_i\) a derivada da subárvore \(T_i\) de \(T\) enraizada em \(X_i\) e \(w_j\) a derivada da subárvore \(T_j\) de \(T\) enraizada em \(X_j\). Evidentemente, \(w_j\) é subpalavra de \(w_i\), assim como \(w_i\) é subpalavra de \(w\). Escrevamos, então, \(w=uvxyz\) de modo que \(vxy=w_i\) e \(x=w_j\). Note-se que, como \(j > i\), não é possível que as palavras \(v\) e \(y\) sejam ambas vazias. Ainda, como a profundidade de \(T_i\) é no máximo \(\lvert V\rvert + 1\), temos que \(\lvert xvy\rvert \leq 2^{\lvert V\rvert}=n\).

Para concluirmos a demonstração, tomemos \(k\in\bN\). Vamos mostrar que \(uv^kxy^kz\) está em \(L(\Gamma)\) e, portanto, em \(L\). Ora, \(uv^kxy^kz\) é exatamente a derivada da árvore de derivação completa obtida a partir de \(T\): trocando-se, se \(k=0\), toda a subárvore \(T_i\) por \(T_j\); trocando-se, se \(k > 0\), toda a subárvore \(T_j\) por \(T_i\) e repetindo esta operação outras \(k-1\) vezes. □

TEOREMA A.4. A linguagem \(L=\{0^n1^n2^n \mathbin : n\in\bN\}\subseteq\{0,1,2\}^{\ast}\) não é livre de contexto.

Demonstração. Suponhamos que \(L\) seja livre de contexto. Tomemos, então, um inteiro positivo \(n\) tal como no enunciado do Lema de Bombeamento para linguagens livres de contexto. Tomemos também \(w=0^n1^n2^n\). Como \(\lvert w\rvert \geq n\), temos que existem \(u,v,x,y,z\in\Sigma^{\ast}\) tais que \(w=uvxyz\) satisfazendo as condições do lema. Em particular, \(uv^0xy^0z=uxz\in L\). No entanto, como \(\lvert vxy\rvert\leq n\), não é possível que a palavra \(vxy\) contenha \(0\)s, \(1\)s, e \(2\)s. Seja \(i\in\{0,1,2\}\) tal que \(vxy\) certamente não contém \(i\), e seja \(j\in\{0,1,2\}\) tal que \(vy\) certamente contém \(j\). Note-se que a existência de \(j\) é garantida, uma vez que \(vy\neq\upeps\). Então, temos que \(\#i(uxz)=\#i(w)\), porém que \(\#j(uxz) < \#j(w)\), uma contradição. □

• Base: [ArBa09] Cap. 1; [Pap93] Sec. 2.1–2.3
• Exercícios: 26–29

DEFINIÇÃO 5.1. Uma Máquina de Turing determinística (MTD) é uma \(6\)-tupla \((Q, \Sigma,\delta,q_0,\def\qyes{q_{\text{sim}}}\qyes,\def\qno{q_{\text{não}}}\qno)\) em que:

• \(Q\) é o conjunto de estados da máquina, um conjunto finito com pelo menos três elementos;
• \(\Sigma\) é o alfabeto da máquina, o qual não pode conter os símbolos especiais reservados \(\def\mtstart{{\rhd}}\mtstart\) e \(\def\mtblank{{\sqcup}}\mtblank\);

• \(\delta\colon (Q\setminus\{\qyes,\qno\})\times(\Sigma\cup\{\mtstart,\mtblank\})\to Q\times(\Sigma\cup\{\mtstart,\mtblank\})\times\{\def\mtleft{{\leftarrow}}\mtleft,\def\mtstay{{\operatorname{–}}}\mtstay,\def\mtright{{\rightarrow}}\mtright\}\) é a função de transição da máquina, a qual define, para o estado não-final em \(Q\setminus\{\qyes,\qno\}\) no qual a máquina se encontra e para o símbolo em \(\Sigma\cup\{\mtstart,\mtblank\}\) que está sendo lido da fita da máquina, qual o próximo estado em \(Q\) para o qual a máquina vai, qual símbolo em \(\Sigma\cup\{\mtstart,\mtblank\}\) deve ser escrito na fita, e qual movimento em \(\{\mtleft,\mtstay,\mtright\}\) o cabeçote da fita deve fazer, satisfazendo, para quaisquer \(p,q\in Q\), \(r,s\in\Sigma\cup\{\mtstart,\mtblank\}\), e \(m\in\{\mtleft,\mtstay,\mtright\}\), a implicação

  \begin{equation*} (\delta(q,s)=(p,r,m))\wedge((s=\mtstart)\vee(r=\mtstart)) \quad\Rightarrow\quad (r=\mtstart)\wedge (m\neq\mtleft)\,; \end{equation*}
• \(q_0\in Q\setminus\{\qyes,\qno\}\) é o estado inicial da máquina;
• \(\qyes\in Q\setminus\{q_0,\qno\}\) é o estado final de aceitação da máquina;
• \(\qno\in Q\setminus\{q_0,\qyes\}\) é o estado final de rejeição da máquina.

DEFINIÇÃO 5.2. Uma configuração (ou descrição instantânea) de uma MTD \((Q,\Sigma,\delta,q_0,\qyes,\qno)\) é uma tripla \((q,w,u)\) em que:

• \(q\in Q\) é o estado da configuração;
• \(w\in (\Sigma\cup\{\mtstart,\mtblank\})^{+}\) é a palavra que representa o conteúdo da fita até o cabeçote;
• \(u\in (\Sigma\cup\{\mtstart,\mtblank\})^{+}\) é a palavra que representa o conteúdo da fita depois do cabeçote.

Uma configuração \(C=(q,w,u)\) é dita final se se \(q\in\{\qyes,\qno\}\). Ainda, a configuração inicial de \(M\) para uma entrada \(x\in\Sigma^{\ast}\) é a configuração \(C_0(M,x)\bydef (q_0,\mtstart,x)\), se \(x\neq\varepsilon\), ou a configuração \((q_0,\mtstart,\mtblank)\), se \(x=\varepsilon\).

Como a computação de uma MTD é determinística, cada configuração não-final alcança exatamente uma configuração.

DEFINIÇÃO 5.3. Sejam \(w_1,w_2,u_1,u_2,w',u'\in(\Sigma\cup\{\mtstart,\mtblank\})^{+}\) e \(s,t\in\Sigma\cup\{\mtstart,\mtblank\}\) tais que \(w_1=w's\) e \(u_1=tu'\). Dizemos que uma configuração \(C_1=(q_1,w_1,u_1)\) alcança uma configuração \(C_2=(q_2,w_2,u_2)\) pela MTD \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\), com \(q_1,q_2\in Q\), e escrevemos \(C_1\underset{M}\Rightarrow C_2\), se ocorre um dos casos a seguir:

• \(\delta(q_1,s)=(q_2,r,\mtright)\), \(w_2=w'rt\), e: \(u_2=u'\) se \(u'\neq\varepsilon\), e \(u_2=\mtblank\) se \(u'=\varepsilon\);
• \(\delta(q_1,s)=(q_2,r,\mtleft)\), \(w_2=w'\), e \(u_2=ru_1\);
• \(\delta(q_1,s)=(q_2,r,\mtstay)\), \(w_2=w'r\), e \(u_2=u_1\).

DEFINIÇÃO 5.4. Sendo \(n\) um inteiro não-negativo e \(C_1\) e \(C_2\) duas configurações de uma MTD \(M\), escrevemos \(C_1\underset M{\overset n\Rightarrow} C_2\), ou simplesmente \(C_1\overset n\Rightarrow C_2\) quando livre de ambiguidade, se \(C_1=C_2\) e \(n=0\), ou se \(n > 0\) e existe alguma configuração \(C_3\) de \(M\) tal que \(C_1\underset M{\overset{n-1}\Rightarrow} C_3\) e \(C_3\underset M\Rightarrow C_2\). Ainda, escrevemos \(C_1\underset M{\overset{\ast}\Rightarrow} C_2\) se existe algum inteiro não-negativo \(n\) tal que \(C_1\underset M{\overset n\Rightarrow} C_2\). Uma computação, ou traçado (ou, no contexto de máquinas determinísticas, execução) de \(M\) para uma entrada \(x\) é uma sequência de configurações \(C_0,C_1,C_2,\dotsc\) tal que:

• \(C_0=C_0(M,x)\);
• para todo par de configurações consecutivas \(C_i\) e \(C_{i+1}\) na sequência, vale que \(C_i\underset M\Rightarrow C_{i+1}\);
• ou a sequência é infinita, ou a última configuração da sequência é uma configuração final.

DEFINIÇÃO 5.5. Sendo \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) uma MTD e \(x\) uma palavra de \(\Sigma^{\ast}\), se \(C_0(M,x)\underset{M}{\overset{\ast}\Rightarrow} C_f\) para alguma configuração final \(C_f=(q,w,u)\), dizemos:

• que \(M\) aceita \(x\) se \(q=\qyes\), e escrevemos \(M(x)=\def\mtyes{\text{sim}}\mtyes\);
• que \(M\) rejeita \(x\) se \(q=\qno\), e escrevemos \(M(x)=\def\mtno{\text{não}}\mtno\);
• que a saída de \(M\) para a entrada \(x\) é \(y\), e escrevemos \(M(x)=y\), se \(y\) é a subpalavra de \(wu\) sobre \(\Sigma\) que se lê a partir da última ocorrência do símbolo \(\mtstart\) em \(wu\) removendo-se todos os símbolos \(\mtblank\) (por exemplo, se \(wu=\mtstart01\mtstart\mtblank10\mtblank111\), \(y=10111\)).

DEFINIÇÃO 5.6. Sendo \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) uma MTD e \(x\) uma palavra de \(\Sigma^{\ast}\), se a computação de \(M\) para \(x\) é infinita, escrevemos \(M(x)=\def\mtup{\nearrow}\mtup\) e dizemos que \(M\) não para para \(x\).

DEFINIÇÃO 5.7. O tempo de uma Máquina de Turing \(M=(Q,\Sigma,\delta,q_0,\qyes)\) para uma entrada \(x\in\Sigma^{\ast}\), denotado por \(t_M(x)\), é número de passos (ou transições) na computação de \(M\) para \(x\), i.e. \(t_M(x)=t\) se e somente se \(C_0(M,x)\underset M{\overset t\Rightarrow}C_f\) para alguma configuração final \(C_f\). A complexidade de tempo uma Máquina de Turing \(M\) para um comprimento de entrada \(n\in\bN\) é:

• uma função \(\funto f{\bN}{\bN}\), e escrevemos \(T_M(n)=f(n)\), se \(t_M(x)=f(n)\) , para toda entrada \(x\) com \(\lvert x\rvert = n\);
• uma classe de funções \(\mathscr C\) de \(\bN\) em \(\bN\), e escrevemos \(T_M(n)=\mathscr C(n)\) (e.g. \(T_M(n)=O(n)\)), se, para toda entrada \(x\) com \(\lvert x\rvert=n\), existe uma função \(f\in\mathscr C\) tal que \(t_M(x)=f(n)\).

Como exemplo, apresentamos a Máquina de Turing \(M\) definida pela tabela de transições a seguir. Esta máquina, dada uma palavra binária \(x\), computa o complemento \(\overline x\) de \(x\).

	\(\mtstart\)	\(0\)	\(1\)	\(\mtblank\)
\(\to q_0\)	\((q_0,\mtstart,\mtright)\)	\((q_0,1,\mtright)\)	\((q_0,0,\mtright)\)	\((\qyes,\mtblank,\mtstay)\)

Considerando a entrada \(x=100\), a configuração inicial de \(M\) para \(x\) é \(C_0=(q_0,\mtstart,100)\), e a computação de \(M\) para \(x\) é:

\begin{align*} (q_0,\mtstart,100)&\Rightarrow (q_0,\mtstart1,00)\\&\Rightarrow (q_0,\mtstart00,0)\\&\Rightarrow (q_0,\mtstart010,\mtblank)\\&\Rightarrow (q_0,\mtstart011\mtblank,\mtblank)\\&\Rightarrow (\qyes,\mtstart011\mtblank,\mtblank)\,. \end{align*}

Consequentemente, \(M(100)=011\). Tomando, por outro exemplo, a entrada \(x=\upeps\), temos

\begin{equation*} (q_0,\mtstart,\mtblank)\underset M\Rightarrow(q_0,\mtstart\mtblank,\mtblank) \underset M\Rightarrow(\qyes,\mtstart\mtblank,\mtblank) \end{equation*}

e \(M(\upeps)=\upeps\). Observe que, para esta Máquina de Turing, temos \(t_M(100)=5\), \(t_M(\upeps)=2\), e \(T_M(n)=n+2\) (e, portanto, \(T_M(n)=O(n)\)), já que, para toda palavra \(x\) com comprimento \(n\geq 0\), a máquina \(M\) faz uma transição para cada bit de \(x\), mais uma transição para o \(\mtblank\) após o último bit de \(x\), mais uma transição para atingir o estado final.

DEFINIÇÃO 5.8. Uma Máquina de Turing determinística com \(k\) fitas (MTD-\(k\)) é uma \(7\)-tupla \((k, Q,\Sigma,\delta,q_0,\qyes,\qno)\) em que:

• \(k\) é um inteiro positivo;
• \(Q\) é o conjunto de estados da máquina, um conjunto finito com pelo menos três elementos;
• \(\Sigma\) é o alfabeto da máquina, o qual não pode conter os símbolos especiais reservados \(\mtstart\) e \(\mtblank\);

• \(\delta\colon (Q\setminus\{\qyes,\qno\})\times(\Sigma\cup\{\mtstart,\mtblank\})^k\to Q\times((\Sigma\cup\{\mtstart,\mtblank\})\times\{\mtleft,\mtstay,\mtright\})^k\) é a função de transição da máquina, de modo que, se

  \begin{equation*} \delta(q,s_1,s_2,\dotsc,s_k)=(p,(r_1,m_1),(r_2,m_2),\dotsc,(r_k,m_k)) \end{equation*}

  e \(\{s_i,r_i\}\cap\{\mtstart\}\neq\emptyset\) para algum \(i\in\{1,\dotsc,k\}\), então \(r_i=\mtstart\) e \(m_i\neq\mtleft\);

• \(q_0\in Q\setminus\{\qyes,\qno\}\) é o estado inicial da máquina;
• \(\qyes\in Q\setminus\{q_0,\qno\}\) é o estado final de aceitação da máquina;
• \(\qno\in Q\setminus\{q_0,\qyes\}\) é o estado final de rejeição da máquina.

DEFINIÇÃO 5.9. Uma configuração (ou descrição instantânea) de uma MTD-\(k\) \((k,Q,\Sigma,\delta,q_0,\qyes,\qno)\) é uma tupla \((q,(w_1,u_1),\dotsc,(w_k,u_k))\) em que:

• \(q\in Q\) é o estado da configuração;
• \(w_i\in (\Sigma\cup\{\mtstart,\mtblank\})^{+}\), para \(1\leq i\leq k\), é a palavra que representa o conteúdo da \(i\)-ésima fita até seu cabeçote;
• \(u_i\in (\Sigma\cup\{\mtstart,\mtblank\})^{+}\), para \(1\leq i\leq k\), é a palavra que representa o conteúdo da \(i\)-ésima fita depois de seu cabeçote.

Uma configuração é dita final se se \(q\in\{\qyes,\qno\}\). A configuração inicial de \(M\) para uma entrada \(x\in\Sigma^{\ast}\) é a configuração \(C_0(M,x)\) definida por:

\begin{align*} (q_0,(\mtstart,x),\overbrace{(\mtstart,\mtblank),\dotsc,(\mtstart,\mtblank)}^{\text{$k-1$ pares}})\,,\quad &\text{se $x\neq\varepsilon$;}\\ (q_0,\overbrace{(\mtstart,\mtblank),\dotsc,(\mtstart,\mtblank)}^{\text{$k$ pares}})\,,\quad &\text{se $x=\varepsilon$.} \end{align*}

Ainda, \(C_0(M,x)\underset{M}{\overset{\ast}\Rightarrow} C_f\) para alguma configuração final \(C_f=(q,(w_1,u_1),\dotsc,(w_k,u_k))\), dizemos:

• que \(M\) aceita \(x\) se \(q=\qyes\), e escrevemos \(M(x)=\mtyes\);
• que \(M\) rejeita \(x\) se \(q=\qno\), e escrevemos \(M(x)=\mtno\);
• que a saída de \(M\) para a entrada \(x\) é \(y\), e escrevemos \(M(x)=y\), se \(y\) é a subpalavra de \(w_ku_k\) sobre \(\Sigma\) que se lê a partir da última ocorrência do símbolo \(\mtstart\) em \(w_ku_k\) removendo-se todos os símbolos \(\mtblank\).

Os conceitos de alcançabilidade entre configurações, computação, aceitação, rejeição, tempo, e complexidade de tempo são definidos para máquinas com múltiplas fitas de modo análogo a como são definidos para máquinas com uma só fita (Definições 5.3–5.7).

Como exemplo, apresentamos a Máquina de Turing com \(2\) fitas definida pela tabela de transições a seguir. Esta máquina decide a linguagem dos palíndromos binários. Observe que, para fim de apresentação, optamos por dispor os estados nas colunas, ao invés de nas linhas, como costumamos fazer. As entradas na tabela marcadas com ‘—’ correspondem a transições inalcançáveis (portanto, qualquer elemento do contradomínio de \(\delta\) que for colocado nestas posições serve), i.e. a configuração inicial de \(M\) para qualquer entrada \(x\) jamais alcança, em qualquer número de passos, uma configuração tomando alguma dessas transições.

	\(\to q_0\)
\((\mtstart,\mtstart)\)	\((q_0,(\mtstart,\mtright),(\mtstart,\mtright))\)
\((\mtstart,0)\)	\(\text —\)
\((\mtstart,1)\)	\(\text —\)
\((\mtstart,\mtblank)\)	\((\qyes,(\mtstart,\mtstay),(\mtblank,\mtstay))\)
\((0,\mtstart)\)	\(\text —\)
\((0,0)\)	\((q_0,(0,\mtleft),(0,\mtright))\)
\((0,1)\)	\((\qno,(1,\mtleft),(0,\mtright))\)
\((0,\mtblank)\)	\((q_0,(0,\mtright),(0,\mtright))\)
\((1,\mtstart)\)	\(\text —\)
\((1,0)\)	\((\qno,(1,\mtleft),(0,\mtright))\)
\((1,1)\)	\((q_0,(1,\mtleft),(1,\mtright))\)
\((1,\mtblank)\)	\((q_0,(1,\mtright),(1,\mtright))\)
\((\mtblank,\mtstart)\)	\((q_0,(\mtblank,\mtleft),(\mtstart,\mtright))\)
\((\mtblank,0)\)	\((q_0,(\mtblank,\mtstay),(0,\mtleft))\)
\((\mtblank,1)\)	\((q_0,(\mtblank,\mtstay),(1,\mtleft))\)
\((\mtblank,\mtblank)\)	\((q_0,(\mtblank,\mtstay),(\mtblank,\mtleft))\)

Vamos fazer a análise da complexidade de tempo desta máquina. Sendo \(x\) uma palavra binária com \(\lvert x\rvert =n\), temos, no pior caso, em que \(x\) é um palíndromo com comprimento, que a máquina faz:

• \(n+1\) transições para alcançar o \(\mtblank\) à direita de \(x\) na 1ª fita, copiando \(x\) para a 2ª fita;
• \(n+1\) transições para alcançar o \(\mtstart\) à esquerda de \(x\) na 2ª fita, mantendo o cabeçote da 1ª fita parado;
• \(n+1\) transições para que o cabeçote da 1ª fita alcance \(\mtstart\) e o cabeçote da 2ª alcance \(\mtblank\);
• \(1\) transição para atingir o estado final.

Logo, \(T_M(n)\leq 3(n+1)+1\) e, consequentemente, \(T_M(n)=O(n)\).

TEOREMA 5.10. Para toda Máquina de Turing \(M\) com múltiplas fitas com complexidade de tempo \(O(f(n))\), existe uma Máquina de Turing \(M'\) com uma só fita com complexidade \(O((n+f(n))^2)\) tal que \(M(x)=M'(x)\) para toda entrada \(x\).

Antes de realizarmos a demonstração deste teorema, observe-se que, se \(f(n)\) é assintoticamente pelo menos \(n\), o que geralmente é o caso, \(O((n+f(n))^2)=O((f(n))^2)\). Por outro lado, se ocorre a exceção de \(f(n)\) ser assintoticamente inferior a \(n\), \(O((n+f(n))^2)=O(n^2)\).

Demonstração do Teorema 5.10. Seja \(M=(k,Q,\Sigma,\delta,q_0,\qyes,\qno)\) uma Máquina de Turing com \(k\) fitas com complexidade de tempo \(O(f(n))\). Vamos descrever uma Máquina de Turing \(M'=(Q',\Sigma',\delta',q'_0,\qyes,\qno)\) com complexidade de tempo \(O((n+f(n))^2)\) tal que \(M'(x)=M(x)\) para toda entrada \(x\).

Como \(M'\) possui só um cabeçote, enquanto que \(M\) possui \(k\) cabeçotes, marcamos a posição de cada cabeçote de \(M\) sublinhando em \(M'\) o símbolo sobre o qual o cabeçote se encontra. Assim, o cabeçote de \(M'\) pode se mover livremente sobre a fita. Observe-se que não precisamos sublinhar \(\mtstart'\), já que \(M'\) saberá que um dos \(k\) cabeçotes de \(M\) se encontra posicionado sobre um \(\mtstart\) se não encontrar símbolo sublinhado algum no trecho correspondente da fita de \(M'\). Sendo, então, \(\underline{\Sigma}\bydef\{\underline s\mathbin :s\in\Sigma\}\), e supondo sem perda de generalidade que \(\Sigma\), \(\underline{\Sigma}\), e \(\{\mtstart',\lhd,\underline{\mtblank}\}\) são conjuntos disjuntos, fazemos \(\Sigma'\bydef\Sigma\cup\underline{\Sigma}\cup\{\mtstart',\lhd,\underline{\mtblank}\}\). A descrição de \(M'\) apresentamos no algoritmo a seguir. No pseudocódigo, armazenar em estado significa que criaremos tantos estados quantos forem necessários para que a informação apreendida não se perca.

\(\underline{M'(x)}\):

1. desloque \(x\) uma posição para a direita, inserindo \(\mtstart'\) à esquerda de \(x\);
2. escreva a palavra \(\lhd(\mtstart'\lhd)^{k-1}\) à direita de \(x\);
3. retorne o cabeçote a \(\mtstart\);
4. armazene em estado a informação de que o estado \(q\) em que se encontra a emulação de \(M\) é \(q_0\);
5. enquanto \(q\) é não-final, faça:
6. \(\quad\)percorra toda a fita \(k\) vezes para inserir um \(\mtblank\) à esquerda de cada \(\lhd\);
7. \(\quad\)retorne o cabeçote a \(\mtstart\);
8. \(\quad\)percorra toda a fita, armazenando em estado os \(k\) símbolos \(s_1,\dotsc,s_k\) sobre os quais se encontram os \(k\) cabeçotes da emulação de \(M\);
9. \(\quad\)retorne o cabeçote a \(\mtstart\);
10. \(\quad\)percorra toda a fita, efetuando as alterações correspondentes à transição \(\delta(q,s_1,\dotsc,s_k)=(q',(r_1,m_1),\dotsc,(r_k,m_k))\);
11. \(\quad\)retorne o cabeçote a \(\mtstart\);
12. \(\quad\)armazene em estado a informação de que o estado \(q\) em que se encontra a emulação de \(M\) é \(q'\);
13. percorra toda a fita, trocando todo símbolo \(\underline s\) por \(s\), e deixando nela apenas o conteúdo \(y\) da última fita de \(M\), escrevendo tantos \(\mtstart\) quantos necessários à esquerda de \(y\) e tantos \(\mtblank\) quantos necessários à direita;
14. pare no mesmo estado final em que parou a emulação de \(M\).

Para verificarmos que de fato \(M(x)=M'(x)\), basta observarmos que:

• se \(M(x)=\mtyes\), temos \(M'(x)=\mtyes\) pela linha 14;
• se \(M(x)=\mtno\), temos \(M'(x)=\mtno\) também pela linha 14;
• se \(M(x)=y\), temos \(M'(x)=y\) pela linha 13;
• se \(M(x)=\mtup\), temos \(M'(x)=\mtup\) pela linha 5.

Vamos agora à análise da complexidade de tempo de \(M'\). Primeiramente, observemos que o tamanho máximo que a fita de \(M'\) pode assumir é \(O(n+kf(n))=O(n+f(n))\), já que cada uma das \(O(f(n))\) instruções que a Máquina \(M\) executa aumenta o tamanho de cada uma das \(k\) fitas em no máximo uma posição. Sendo \(n\) o comprimento da entrada \(x\), temos que:

• as linhas 1–4 custam \(2(n+2k+1)=O(n)\) instruções;
• o laço da linha 5 é iterado \(O(f(n))\) vezes, sendo que cada iteração custa:
  • a linha 6 custa tantas instruções quanto o tamanho da fita de \(M'\), o qual, como já explicamos, é \(O(n+f(n))\), vezes \(k\), totalizando tempo \(O(k(n+f(n)))\);
  • as linha 7–11 também custam tempo \(O(n+f(n))\);
  • a linha 12 custa tempo \(O(1)\);
• as linhas 13–14 custam tempo \(O(n+f(n))\).

Concluímos, portanto, que a complexidade de tempo de \(M'\) é

\begin{align*} T_M(n)&=O(n)+ O(f(n))\bigl(O(k(n+f(n)))+O(n+f(n))+O(1)\bigr)+O(n+f(n))\\ &=O((n+f(n))^2)\,, \end{align*}

como queríamos. □

DEFINIÇÃO 5.11. Uma Máquina de Turing não-determinística (MTN) é uma \(6\)-tupla \((Q,\Sigma,\Delta,q_0,\qyes,\qno)\) em que:

• \(Q\) é o conjunto de estados da máquina, um conjunto finito com pelo menos três elementos;
• \(\Sigma\) é o alfabeto da máquina, o qual não pode conter os símbolos especiais reservados \(\mtstart\) e \(\mtblank\);

• \(\Delta\) é a relação de transição da máquina, uma relação binária de \((Q\setminus\{\qyes,\qno\})\times(\Sigma\cup\{\mtstart,\mtblank\})\) para \(Q\times(\Sigma\cup\{\mtstart,\mtblank\})\times\{\mtleft,\mtstay,\mtright\}\), de modo que, se

  \begin{equation*} ((q,s)\Delta(p,r,m))\wedge((s=\mtstart)\vee(r=\mtstart))\,, \end{equation*}

  então \(r=\mtstart\) e \(m\neq\mtleft\);

• \(q_0\in Q\setminus\{\qyes,\qno\}\) é o estado inicial da máquina;
• \(\qyes\in Q\setminus\{q_0,\qno\}\) é o estado final de aceitação da máquina;
• \(\qno\in Q\setminus\{q_0,\qyes\}\) é o estado final de rejeição da máquina.

Analogamente à Definição 5.8, podemos definir o conceito de Máquina de Turing não-determinística com \(k\) fitas. Conceitos como configuração, alcançabilidade entre configurações, e computação também são definidos para máquinas não-determinísticas analogamente aos que foram apresentados para máquinas determinísticas. Note-se que, como se trata de um modelo não-determinístico, pode haver várias computações possíveis de uma máquina para uma mesma entrada.

DEFINIÇÃO 5.12. Sejam \(N=(Q,\Sigma,\Delta,q_0,\qyes,\qno)\) uma Máquina de Turing não-determinística e \(x\in\Sigma^{\ast}\).

• Dizemos que \(N\) aceita \(x\), e escrevemos \(N(x)=\mtyes\), se alguma computação de \(N\) para \(x\) que termina em aceitação (ainda que haja outras computações de \(N\) para \(x\) que terminem em rejeição, ou mesmo que sejam infinitas).
• Dizemos que \(N\) rejeita \(x\), e escrevemos \(N(x)=\mtno\), se toda computação de \(N\) para \(x\) termina em rejeição.
• Dizemos que \(N\) não para para \(x\), e escrevemos \(N(x)=\mtup\), se:
  1. existe alguma computação infinita de \(N\) para \(x\);
  2. toda (se alguma) computação finita de \(N\) para \(x\) termina em rejeição.
• Dizemos que a saída de \(N\) para a entrada \(x\) é \(y\), e escrevemos \(N(x)=y\), se:
  1. existe alguma computação de \(N\) para \(x\) que termina em aceitação;
  2. em toda configuração final de aceitação alcançável a partir da configuração inicial de \(N\) para \(x\), a palavra \(y\) é a subpalavra de \(wu\) sobre \(\Sigma\) que se lê a partir da última ocorrência do símbolo \(\mtstart\) em \(wu\) removendo-se todos os símbolos \(\mtblank\).

O tempo de \(N\) para \(x\), denotado por \(t_N(x)\), é o comprimento (número de transições, ou passos) da maior computação de \(N\) para \(x\). A complexidade de tempo de \(N\) é definida analogamente à Definição 5.7.

TEOREMA 5.13. Para toda Máquina de Turing não-determinística \(N\) com complexidade de tempo \(O(f(n))\), existem uma constante real \(c > 1\) (que depende de \(N\)) e uma Máquina de Turing determinística \(M\) com complexidade \(O(c^{n+f(n)})\) tal que \(M(x)=N(x)\) para toda entrada \(x\).

Demonstração. Seja \(N=(Q,\Sigma,\Delta,q_0,\qyes,\qno)\) uma MTN e seja \(d_N\bydef\max_{q,s}\lvert\Delta(q,s)\rvert\). Vamos construir uma MTD \(M=(k,\Sigma',Q',\delta,q'_0,\qyes,\qno)\) com no mínimo três fitas e complexidade de tempo \(O(c^{n+f(n)})\), para alguma constante \(c > 1\), tal que \(M(x)=N(x)\) para todo \(x\in\Sigma^{\ast}\). Para tanto, notemos que, para todo inteiro positivo \(t\), uma sequência de \(t+1\) configurações encadeadas \(C_0\underset N\Rightarrow\dotsb\underset N\Rightarrow C_t\), com \(C_t\) não necessariamente final, é determinada pelas \(t\) escolhas feitas em cada transição. Isto se observa pois, indexando todas as escolhas em

\begin{equation*} \Delta(q,s)=\{\Delta_0(q,s),\dotsc,\Delta_{d_N(q,s)-1}(q,s)\}\quad \text{para todo $q$ e todo $s$,} \end{equation*}

sendo \(d_N(q,s)\bydef\lvert\Delta(q,s)\rvert\leq d_N\), a sequência de \(t+1\) configurações \(C_0\underset N\Rightarrow\dotsb\underset N\Rightarrow C_t\), pode ser designada por \(t\) inteiros \(i_1,\dotsc,i_t\in\{0,\dotsc,d_N-1\}\), os quais representam, respectivamente, as escolhas feitas nas \(t\) transições. Ainda, uma sequência de \(t\) inteiros \(i_1,\dotsc,i_t\in\{0,\dotsc,d_N-1\}\) pode ser entendida como uma palavra sobre o alfabeto \(\{0,\dotsc,d_N-1\}\), uma vez que \(d_N\) é uma constante que depende unicamente de \(N\). Assim, o que nossa máquina determinística \(M\) faz para uma entrada \(x\) é enumerar todas as palavras sobre \(\{0,\dotsc,d_N-1\}\), em ordem crescente lexicográfica, emulando \(N\) para \(x\) de acordo com cada sequência de escolhas enumerada. O funcionamento de \(M\) descrevemos no pseudocódigo a seguir, fazendo \(\Sigma'\bydef\Sigma\cup\{0,\dotsc,d_N-1\}\). No pseudocódigo, \(s_j\) corresponde ao símbolo lido da \(j\)-ésima fita de \(M\).

\(\underline{M(x)}\):

1. \(t\leftarrow 1\);
2. \(continue\leftarrow\def\btrue{\mathsf V}\btrue\);
3. enquanto \(continue\), faça:
4. \(\quad\) \(continue\leftarrow\def\bfalse{\mathsf F}\bfalse\);
5. \(\quad\) escreva a palavra \(0^t\) na 2ª fita;
6. \(\quad\) \(overflow\leftarrow\bfalse\);
7. \(\quad\) repita:
8. \(\quad\)\(\quad\) posicione o cabeçote da 2ª fita sobre o primeiro símbolo após \(\mtstart\);
9. \(\quad\)\(\quad\) copie \(x\) para a 3ª fita, retornando o cabeçote da 3ª fita a \(\mtstart\);
10. \(\quad\)\(\quad\) \(q\leftarrow q_0\);
11. \(\quad\)\(\quad\) \(v\acute alido\leftarrow \btrue\);
12. \(\quad\)\(\quad\) enquanto \(s_2\neq\mtblank\) e \(q\) não-final e \(v\acute alido\), faça:
13. \(\quad\)\(\quad\)\(\quad\) se \({s_2} < \lvert{\Delta(q,s_3)}\rvert\), entao:
14. \(\quad\)\(\quad\)\(\quad\)\(\quad\) opere na 3ª fita a escolha \(\Delta_{s_2}(q,s_3)\), atualizando \(q\) e movendo o cabeçote da 2ª fita para a direita;
15. \(\quad\)\(\quad\)\(\quad\) senão, \(v\acute alido\leftarrow\bfalse\);
16. \(\quad\)\(\quad\) se \(q=\qyes\), então, devolva \(\mtyes\);
17. \(\quad\)\(\quad\) se \(q\) não-final e \(v\acute alido\), então, \(continue\leftarrow\btrue\);
18. \(\quad\)\(\quad\) se o conteúdo da 2ª fita for \((d_N-1)^t\), então, \(overflow\leftarrow\btrue\);
19. \(\quad\)\(\quad\) senão, some o conteúdo da 2ª fita com \(1\);
20. \(\quad\) até que \(overflow\);
21. \(\quad\) \(t\leftarrow t + 1\);
22. devolva \(\mtno\).

Como se pode ver, a Máquina \(M\) usa a 2ª fita para armazenar a sequência de índices de escolhas considerada, e a 3ª fita como rascunho para simular a fita de \(N\), já que precisa manter intacta a 1ª fita para restaurá-la para cada uma das próximas sequências de índices de escolhas. Se \(N(x)=\mtyes\), então, existe uma computação de \(N\) para \(x\) com \(t\) transições, para algum \(t\), que termina em \(\qyes\), e a máquina \(M\) eventualmente emulará essa computação até o fim e responderá também \(\mtyes\). Se \(N(x)=\mtno\), então, após a iteração para \(t=t_N(x)\), a máquina \(M\) perceberá que não há mais como expandir as sequências encadeadas de configurações e, por não haver encontrado computação alguma que parasse em \(\qyes\), parará em \(\qno\). Se \(N(x)=\mtup\), então, \(t\) nunca será suficientemente grande para que todas as computações exploradas com comprimento \(t\) atinjam estado final, e também a emulação nunca encontrará alguma computação que termine em aceitação; portanto, também teremos \(M(x)=\mtup\).

Sendo \(n\) o comprimento da entrada \(x\), temos que:

• cada iteração do laço da linha 12 (linhas 13–15) custa tempo \(O(1)\), e, como o laço é iterado no pior caso \(t\) vezes, temos que o tempo das linhas 12–15 é \(O(t)\);
• o tempo das linhas 8–11 é \(O(n)\);
• o tempo das linhas 16–19 é \(O(t)\);
• o tempo total de cada iteração do laço da linha 7 (linhas 8–19) é \(O(n+t)\), e, como o laço é iterado \(d_N^t\) vezes, o tempo das linhas 7–20 é \(O((n+t)d_N^t)\);
• o tempo das linhas 4–6 é \(O(t)\);
• o tempo da linha 21 é \(O(t)\);
• o tempo total de cada iteração do laço da linha 3 (linhas 4–21) é \(O(t+(n+t)d_N^t)=O((n+t)d_N^t)\).

Portanto, como o tempo das linhas 1–2 e 22 é \(O(1)\), e como o laço é iterado no pior caso para todo \(t\) em \(\{1,\dotsc,O(f(n))\}\), temos que

\begin{equation*} \begin{aligned} T_M(n)&\leq\sum_{t=1}^{O(f(n))}O((n+t)d_N^t)\\ &\leq O\biggl((n+f(n))\sum_{t=1}^{O(f(n))}d_N^t\biggr) \\&= O\Bigl((n+f(n))\Bigl(\frac{d_N^{O(f(n))+1}-1}{d_N-1}-1\Bigr)\Bigr)\\&= O((n+f(n))d_N^{O(f(n))+1})\\&=O(d_N^{n+O(f(n))+1}d_N^{n+O(f(n))+1})\\ &=O(d_N^{O(n+f(n))})=O(c^{n+f(n)})\,, \end{aligned} \end{equation*}

para alguma constante real \(c > 1\), como queríamos mostrar. □

• Base: [ArBa09] Sec. 1.3–1.4; [Pap93] Cap. 2–3
• Exercícios: 30–38

DEFINIÇÃO 6.1. Dizemos que uma Máquina de Turing (determinística ou não-determinística) \(M\) com alfabeto \(\Sigma\) resolve um problema computacional \((\mathscr I,\mathscr S, f)\), sendo \(f\) uma função, sob uma função de codificação \(\funto{\langle\rangle}{\mathscr I\cup\mathscr S}{\Sigma^{\ast}}\), se \(M(\langle x\rangle)=\langle{f(x)}\rangle\) para todo \(x\in \mathscr I\). Neste caso, também dizemos que \(M\) computa \(f\). No caso particular de problemas de decisão, dizemos que \(M\) decide uma linguagem \(L\subseteq \Sigma^{\ast}\) se, para todo \(x\in L\), temos \(M(x)=\mtyes\) e, para todo \(x\notin L\), temos \(M(x)=\mtno\).

DEFINIÇÃO 6.2 (Tese de Church–Turing). Uma função de domínio e contradomínio enumeráveis é dita computável se existe uma Máquina de Turing que a computa.

DEFINIÇÃO 6.3. Sendo \(M\) uma Máquina de Turing (determinística ou não-determinística) com alfabeto \(\Sigma\), definimos

\begin{align*} L(M)&\bydef \{ x\in\Sigma^{\ast}\mathbin : M(x)=\mtyes\}\,,\\ \overline L(M)&\bydef \{ x\in\Sigma^{\ast}\mathbin : M(x)=\mtno\}\,.\\ \end{align*}

Observe que uma Máquina de Turing \(M\) decide uma linguagem \(L\) se e somente se \(L(M)=L\) e \(\overline L(M)=\Sigma^{\ast}\setminus L\).

DEFINIÇÃO 6.4, Uma função de domínio e contradomínio enumeráveis é dita recursiva se é computável. Uma linguagem \(L\) é dita recursiva, ou decidível, se existe uma Máquina de Turing \(M\) que a decide. Um problema de decisão é dito decidível se sua linguagem associada é decidível. A classe das linguagens recursivas (sobre um alfabeto \(\Sigma\)) é denotada por \(\mathsf R\).

Observe que, na Definição 6.4, pouco importa o alfabeto \(\Sigma\) em questão, uma vez que, se uma linguagem sobre um alfabeto \(\Sigma\) é recursiva, então a linguagem correspondente (no sentido do Exercício 3) sobre um outro alfabeto \(\Sigma'\) qualquer também é recursiva.

DEFINIÇÃO 6.5. Sendo \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) uma MTD, e representando-se

• os símbolos de \(\Sigma=\{s_0,\dotsc,s_{\lvert{\Sigma}\rvert-1}\}\) pelos inteiros \(i(s_0)\bydef0,\dotsc,i(s_{\lvert{\Sigma}\rvert-1})\bydef\lvert{\Sigma}\rvert-1\),
• os estados de \(Q\setminus\{\qyes,\qno\}=\{q_0,\dotsc,q_{\lvert Q\rvert-3}\}\) pelos inteiros \(i(q_0)\bydef\lvert{\Sigma}\rvert,\dotsc,i(q_{\lvert Q\rvert-3})\bydef\lvert{\Sigma}\rvert+\lvert{Q}\rvert-3\),
• os estados finais \(\qyes\) e \(\qno\) respectivamente pelos inteiros \(i(\qyes)=\lvert{\Sigma}\rvert+\lvert Q\rvert-2\) e \(i(\qno)=\lvert{\Sigma}\rvert+\lvert Q\rvert-1\),
• os símbolos especiais \(\mtstart\) e \(\mtblank\) respectivamente pelos inteiros \(i(\mtstart)=\lvert{\Sigma}\rvert+\lvert Q\rvert\) e \(i(\mtblank)=\lvert{\Sigma}\rvert+\lvert Q\rvert+1\),
• os movimentos de cabeçote \(\mtleft\), \(\mtstay\) e \(\mtright\) respectivamente pelos inteiros \(i(\mtleft)=\lvert{\Sigma}\rvert+\lvert Q\rvert+2\), \(i(\mtstay)=\lvert{\Sigma}\rvert+\lvert Q\rvert+3\) e \(i(\mtright)=\lvert{\Sigma}\rvert+\lvert Q\rvert+4\),

a codificação de \(M\) no alfabeto \(\Sigma_U=\{0,1,{,},{;},(,)\}\), denotada por \(\langle M\rangle_U\), ou simplesmente \(\langle M\rangle\) quando livre de ambiguidade, é definida

1. pela representação em binário do inteiro \(\lvert Q\rvert\), seguida
2. de uma vírgula, seguida
3. da representação em binário do inteiro \(\lvert{\Sigma}\rvert\), seguida
4. de outra vírgula, seguida
5. da concatenação das codificações das transições de \(\delta\), separando-se codificações consecutivas por uma vírgula, sendo a codificação de cada transição \(\delta(q,s)=(q',s',m)\) definida
   1. por dois símbolos de abertura de parêntese, seguidos
   2. da codificação em binário com exatos \(\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\) bits de \(i(q)\), seguida
   3. de uma vírgula, seguida
   4. da codificação em binário com exatos \(\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\) bits de \(i(s)\), seguida
   5. de um símbolo de fechamento de parêntese, uma vírgula e um símbolo de abertura de parêntese, seguidos
   6. da codificação em binário com exatos \(\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\) bits de \(i(q')\), seguida
   7. de uma vírgula, seguida
   8. da codificação em binário com exatos \(\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\) bits de \(i(s')\), seguida
   9. de uma vírgula, seguida
   10. da codificação em binário com exatos \(\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\) bits de \(i(m)\), seguida
   11. de dois símbolos de fechamento de parêntese.

Por exemplo, seja \(M\) a MTD definida pela tabela de transições a seguir.

	\(\mtstart\)	\(0\)	\(1\)	\(\mtblank\)
\(\to q_0\)	\((q_0,\mtstart,\mtright)\)	\((q_0,1,\mtright)\)	\((q_0,0,\mtright)\)	\((\qyes,\mtblank,\mtstay)\)

Neste caso, temos

\begin{align*} \langle M\rangle =&11,10,\\ &((0010,0101),(0010,0101,1001)),\\ &((0010,0000),(0010,0001,1001)),\\ &((0010,0001),(0010,0000,1001)),\\ &((0010,0110),(0011,0110,1000))\,. \end{align*}

DEFINIÇÃO 6.6. A Máquina de Turing Universal \(U=(k,Q_U,\Sigma_U,\delta_U,q_{0_U},\qyes,\qno)\), com \(\Sigma_U=\{0,1,{,},{;},(,)\}\), é a MTD com tantas fitas quantas necessárias descrita no pseudocódigo a seguir, a qual, recebendo \(\langle M\rangle{;}x\) como entrada, emula a computação de \(M\) para \(x\). No pseudocódigo, \(\langle\rangle^t\) representa uma codificação binária com exatos \(t\) bits. Ainda, supomos sem perda de generalidade que o alfabeto de toda máquina \(M\) que \(U\) recebe é o alfabeto \(\{0,1\}\).

\(\underline{U(\langle M\rangle{;}x)}\):

1. leia \(\langle M\rangle\), fazendo \(t\leftarrow\lceil\lg(\lvert{\Sigma}\rvert+\lvert Q\rvert+5)\rceil\);
2. escreva \((\langle{i(q_0)}\rangle^t,\langle{i(\mtstart)}\rangle^t,X)\) na 2ª fita, sendo \(X\) a palavra binária obtida trocando-se todos os símbolos \(s\) de \(x\) por \(\langle{i(s)}\rangle^t\), retornando o cabeçote da 2ª fita a \(\mtstart\);
3. \(q\leftarrow q_0\);
4. \(s\leftarrow\mtstart\);
5. enquanto \(q\) for não-final, faça:
6. \(\quad\)encontre \(((\langle{i(q)}\rangle^t,\langle{i(s)}\rangle^t),(\langle{i(q')}\rangle^t,\langle{i(s')}\rangle^t,\langle{i(m)}\rangle^t))\) na 1ª fita;
7. \(\quad\)emule a transição \(\delta(q,s)=(q',s',m)\), atualizando \(q\), \(s\), e a configuração armazenada na 2ª fita, e retornando o cabeçote da 2ª fita a \(\mtstart\);
8. escreva na última fita de \(U\) a concatenação de \(w\) com \(u\), sendo \((\langle{i(q)}\rangle,W,U)\) o conteúdo da 2ª fita, \(w\) a palavra obtida trocando-se cada \(\langle{i(s)}\rangle^t\) de \(W\) por \(s\), e \(u\) a palavra obtida trocando-se cada \(\langle{i(s)}\rangle^t\) de \(U\) por \(s\);
9. pare em \(q\).

Segue imediatamente da Definição 6.6 o Teorema 6.7.

TEOREMA 6.7. Para toda entrada \(\langle M\rangle{;}x\) que a Máquina de Turing Universal \(U\) receba, \(U(\langle M\rangle{;}x)=M(x)\). □

TEOREMA 6.8. A classe \(\mathsf R\) é enumerável, enquanto que a classe de todas as linguagens não.

Demonstração. Seja \(\Sigma\) um alfabeto. Por definição, para toda linguagem recursiva \(L\) sobre \(\Sigma\), existe ao menos uma Máquina de Turing \(M\) cujo alfabeto é \(\Sigma\) tal que \(L(M)=L\) e \(\overline L(M)=\Sigma^{\ast}\setminus L\). Assim, existe uma injeção de \(\mathsf R\) no conjunto \(\mathcal M\) de todas as Máquinas de Turing com alfabeto \(\Sigma\). Por sua vez, toda Máquina de Turing pode ser representada como uma palavra de \(\Sigma_U^{\ast}\), e, como \(\Sigma^{\ast}\) é enumerável para qualquer alfabeto \(\Sigma\), temos que \(\mathsf R\) é enumerável. No entanto, a classe de todas as linguagens é o conjunto \(2^{{\Sigma}^{\ast}}\) (i.e. o conjunto das partes de \(\Sigma^{\ast}\)), um conjunto não-enumerável. □

O Problema da Parada é o problema de decisão definido por: Dada uma Máquina de Turing \(M\) e uma entrada \(x\) para \(M\), vale que \(M\) para para \(x\)? A linguagem associada a este problema denotamos por \(\mathrm{HALTING}\), i.e.

\begin{equation*} \mathrm{HALTING}=\{\langle M\rangle{;}x\mathbin : M(x)\neq\nearrow\}\,. \end{equation*}

TEOREMA 6.9. O Problema da Parada não é decidível.

Demonstração. Suponhamos, a fim de contradição, que exista uma Máquina de Turing \(H\) que decida \(\mathrm{HALTING}\), i.e.

\begin{equation*} H(\langle M\rangle{;}x)=\left\{\begin{aligned} &\mtyes\,,&&\text{para todo $\langle M\rangle{;}x\in\mathrm{HALTING}$,}\\ &\mtno\,,&&\text{para todo $\langle M\rangle{;}x\notin\mathrm{HALTING}$,} \end{aligned}\right. \end{equation*}

Com a Máquina \(H\), construamos então a Máquina de Turing \(D\) descrita pelo pseudocódigo a seguir, a qual possui um estado especial \(q_{\mtup}\) tal que, uma vez entrando neste estado, a Máquina \(D\) jamais sai dele, movendo o cabeçote infinitamente para a direita.

\(\underline{D(\langle M\rangle)}\):

1. emule a Máquina \(H\) para a entrada \(\langle M\rangle{;}\langle M\rangle\);
2. se \(H(\langle M\rangle{;}\langle M\rangle)=\mtno\), devolva \(\mtyes\);
3. entre em \(q_{\mtup}\).

Analisemos agora o que ocorre com a Máquina \(D\) quando recebe \(\langle D\rangle\) como entrada.

• se \(D\) para para \(\langle D\rangle\), então, \(H(\langle D\rangle{;}\langle D\rangle)=\mtyes\), e a computação de \(D\) para \(\langle D\rangle\) entra no estado \(q_{\mtup}\); portanto, \(D\) não para para \(\langle D\rangle\), uma contradição;
• se \(D\) não para para \(\langle D\rangle\), então, \(H(\langle D\rangle{;}\langle D\rangle)=\mtno\), e a computação de \(D\) para \(\langle D\rangle\) move para o estado \(\qyes\); portanto, \(D\) para para \(\langle D\rangle\), também uma contradição.

Como chegamos numa contradição nas duas únicas possibilidades, temos que \(H\) não pode existir. Logo, \(\mathrm{HALTING}\) é indecidível. □

DEFINIÇÃO 6.10. Uma Máquina de Turing \(R=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) é uma redução de uma linguagem \(L_1\subseteq\Sigma^{\ast}\) a uma linguagem \(L_2\subseteq\Sigma^{\ast}\), e escrevemos \(L_1\prec_R L_2\), se vale que

\begin{equation*} x\in L_1\quad\text{se e somente se}\quad R(x)\in L_2\,. \end{equation*}

LEMA 6.11. Se existe uma redução \(R\) de uma linguagem indecidível \(L_1\) a uma linguagem \(L_2\), então \(L_2\) também é indecidível.

Demonstração. Por contraposição, suponhamos que \(L_2\) seja decidível, i.e. que exista uma Máquina de Turing \(M\) que decida \(L_2\). Para mostrarmos que \(L_1\) também é decidível, basta tomarmos a Máquina de Turing \(M'\), definida pelo pseudocódigo a seguir.

\(\underline{M'(x)}\):

1. emule \(R\) para a entrada \(x\), obtendo a saída \(R(x)\);
2. emule \(M\) para a entrada \(R(x)\), obtendo a saída \(M(R(x))\),
3. devolva \(M(R(x))\).

Se \(x\in L_1\), então \(R(x)\in L_2\) e, portanto, \(M'(x)=M(R(x))=\mtyes\). Se \(x\notin L_1\), então \(R(x)\notin L_2\) e, portanto, \(M'(x)=M(R(x))=\mtno\). Portanto, \(M'\) decide \(L_1\). □

Observe que a necessidade do Lema 6.11 nem sempre é verdadeira: se existe uma redução \(R\) de uma linguagem \(L_1\) a uma linguagem \(L_2\) e \(L_2\) é indecidível, então não necessariamente \(L_1\) também é indecidível (veja o Exercício 33).

O Problema da Parada Total é o problema de decisão definido por: Dada uma Máquina de Turing \(M\), vale que \(M\) para para toda entrada \(x\)? A linguagem associada a este problema denotamos por \(\mathrm{HALTING}_T\), i.e.

\begin{equation*} \mathrm{HALTING}_T=\{\langle M\rangle\mathbin : M(x)\neq\nearrow\text{ para todo $x\in\Sigma^{\ast}$}\}\,. \end{equation*}

TEOREMA 6.12. O Problema da Parada Total não é decidível.

Demonstração. Vamos mostrar uma redução \(R\) pela qual \(\mathrm{HALTING}\prec_R\mathrm{HALTING}_T\). Descrevemos \(R\) no pseudocódigo a seguir.

\(\underline{R(\langle M\rangle{;}x)}\):

1. construa a Máquina de Turing \(M'\) descrita por:

   \(\underline{M'(y)}\):

   1. se \(y=x\), então:
   2. \(\quad\) emule \(M\) para \(x\);
   3. \(\quad\) pare no mesmo estado final em que parou a emulação de \(M\) para \(x\);
   4. devolva \(\mtyes\).
2. devolva \(\langle M'\rangle\).

Para mostrarmos que \(R\) de fato é uma redução de \(\mathrm{HALTING}\) para \(\mathrm{HALTING}_T\), basta notarmos que:

• se \(\langle M\rangle{;}x\in\mathrm{HALTING}\), então \(M\) para para \(x\), e a Máquina \(M'\), construída por \(R\) em função de \(M\) e de \(x\), para para \(x\) e para para toda entrada \(y\neq x\), o que nos traz que \(R(\langle M\rangle{;}x)=\langle{M'}\rangle\in\mathrm{HALTING}_T\);
• se \(\langle M\rangle{;}x\notin\mathrm{HALTING}\), então \(M\) não para para \(x\), e a Máquina \(M'\), construída por \(R\) em função de \(M\) e de \(x\), para para toda entrada \(y\neq x\), mas não para para \(x\), o que nos traz que \(R(\langle M\rangle{;}x)=\langle{M'}\rangle\notin\mathrm{HALTING}_T\). □

DEFINIÇÃO 6.13. Dizemos que uma Máquina de Turing \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) aceita uma linguagem \(L\subseteq\Sigma^{\ast}\) se, para todo \(x\in L\), temos \(M(x)=\mtyes\) e, para todo \(x\notin L\), temos \(M(x)=\mtup\).

DEFINIÇÃO 6.14 Uma linguagem \(L\) é dita recursivamente enumerável se existe uma Máquina de Turing \(M\) que a aceita. A classe das linguagens recursivamente enumeráveis é denotada por \(\mathsf{RE}\). Sendo o complementar, ou complemento, de uma linguagem \(L\subseteq\Sigma^{\ast}\) denotado e definido por \(\overline L\bydef\Sigma^{\ast}\setminus L\), a classe das linguagens complementares das linguagens recursivamente enumeráveis é denotada por \(\mathsf{coRE}\).

TEOREMA 6.15. A linguagem do Problema da Parada é recursivamente enumerável.

Demonstração. Seja \(U^{\mtyes}\) a Máquina de Turing obtida a partir da Máquina Universal \(U\) (Definição 6.6) apenas fazendo com que toda transição que conduz a \(\qno\) conduza a \(\qyes\). Temos que:

1. se \(\langle M\rangle{;}x\in\mathrm{HALTING}\), então, \(M\) para para \(x\), e \(U^{\mtyes}\) devolve \(\mtyes\) para a entrada \(\langle M\rangle{;}x\), independentemente do estado final em que tenha parado a emulação de \(M\) para \(x\);
2. se \(\langle M\rangle{;}x\notin\mathrm{HALTING}\), então, a emulação que \(U^{\mtyes}\) faz de \(M\) para \(x\) ao receber \(\langle M\rangle{;}x\) nunca para.

Assim, \(U^{\mtyes}=\mtyes\) para todo \(\langle M\rangle{;}x\in\mathrm{HALTING}\) e \(U^{\mtyes}=\mtup\) para todo \(\langle M\rangle{;}x\notin\mathrm{HALTING}\). □

TEOREMA 6.16. \(\mathsf{RE}\cap\mathsf{coRE}=\mathsf{R}\).

Demonstração. Vamos primeiro mostrar que \(\mathsf{RE}\cap\mathsf{coRE}\subseteq\mathsf{R}\). Seja \(L\) uma linguagem em \(\mathsf{RE}\cap\mathsf{coRE}\), o que significa que existem uma Máquina de Turing \(M_1\) que aceita \(L\) e outra Máquina de Turing \(M_2\) que aceita \(\overline L\). Construamos, então, uma Máquina \(M\) conforme o pseudocódigo a seguir.

\(\underline{M(x)}\):

1. \(j\leftarrow 1\);
2. repita indefinidamente:
3. \(\quad\) emule \(M_1\) para \(x\) por no máximo \(j\) passos;
4. \(\quad\) se a emulação atingiu estado final, devolva \(\mtyes\);
5. \(\quad\) emule \(M_2\) para \(x\) por no máximo \(j\) passos;
6. \(\quad\) se a emulação atingiu estado final, devolva \(\mtno\);
7. \(\quad\) \(j\leftarrow j+1\).

Se \(x\in L\), então a computação de \(M_2\) para \(x\) não para, e existe um \(j\) suficientemente grande para o qual a emulação de \(M_1\) para \(x\) atinge estado final, fazendo \(M\) devolver \(\mtyes\). Se \(x\notin L\), então a computação de \(M_1\) para \(x\) não para, e existe um \(j\) suficientemente grande para o qual a emulação de \(M_2\) para \(x\) atinge estado final, fazendo \(M\) devolver não.

Para concluirmos a demonstração, basta mostrarmos que \(\mathsf R\subseteq\mathsf{RE}\cap\mathsf{coRE}\). Seja \(L\) uma linguagem recursiva e \(M\) uma Máquina de Turing que decide \(L\). Ora, é imediato que \(L\in\mathsf{RE}\), pois se fizermos toda transição que conduz a \(\qno\) conduzir a um estado especial de não-parada \(q_{\mtup}\), obteremos uma Máquina de Turing que aceita \(L\). Assim, \(\mathsf R\subseteq\mathsf{RE}\). Também é imediato que \(\overline L\in\mathsf{R}\), pois se fizermos toda transição que conduz a \(\qno\) conduzir a \(\qyes\) e vice-versa, obteremos uma Máquina de Turing que decide \(\overline L\). Logo, como mostramos que \(\overline L\in\mathsf{R}\) e que \(\mathsf R\subseteq \mathsf{RE}\), temos \(\overline L\in\mathsf{RE}\) e, portanto, \(L\in\mathsf{coRE}\). □

COROLÁRIO 6.17. \(\overline{\mathrm{HALTING}}\) não é recursivamente enumerável. □

DEFINIÇÃO 6.18. Seja \(M=(k,Q,\Sigma,\delta,q_0,\qyes,\qno)\) uma Máquina de Turing, e seja \(C_0\) a configuração inicial de \(M\) para \(\upeps\). Dizemos que \(M\) enumera uma palavra \(x\in\Sigma^{\ast}\) se existem \(q\in Q\) e \(w_1,u_1,\dotsc,w_{k-1},u_{k-1},z\in\Sigma^{\ast}\) tais que

\begin{equation*} C_0\underset{M}{\overset{\ast}\Rightarrow} (q,(w_1,u_1),\dotsc,(w_{k-1},u_{k-1}),(z\mtblank x\mtblank,\mtblank))\,. \end{equation*}

Ainda, a linguagem enumerada por \(M\), ou a linguagem que \(M\) enumera, denotada por \(E(M)\), é a linguagem formada por todas as palavras que \(M\) enumera.

TEOREMA 6.19. Uma linguagem \(L\) é recursivamente enumerável se e somente se existe uma Máquina de Turing que enumera \(L\).

Demonstração. (Suficiência) Suponhamos que exista uma Máquina de Turing \(M=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) que aceite \(L\). Assim, com a Máquina \(M\) podemos construir uma Máquina de Turing \(E_L\) que enumera \(L\), conforme pseudocódigo a seguir, considerando as palavras de \(\Sigma^{\ast}\) tomadas na linha 3 segundo a ordem lexicográfica.

\(\underline{E_L(y)}\):

1. \(j\leftarrow 1\);
2. repita indefinidamente:
3. \(\quad\) para toda palavra \(x\) entre as \(j\) primeiras palavras de \(\Sigma^{\ast}\), faça:
4. \(\quad\)\(\quad\) emule \(M\) para \(x\) por no máximo \(j\) transições;
5. \(\quad\)\(\quad\) se a emulação atingiu estado final, então:
6. \(\quad\)\(\quad\)\(\quad\) escreva \(\mtblank x\mtblank\) no fim da última fita;
7. \(\quad\)\(j\leftarrow j + 1\).

Para toda palavra \(x\in L\), existe algum \(i\) para o qual \(x\) seja a \(i\)-ésima palavra de \(\Sigma^{\ast}\), e, quando \(j\) é tomado \(\max\{i,t_M(x)\}\), a emulação de \(M\) para \(x\) atinge estado final (de aceitação) e a execução de \(E_L\) para \(\upeps\) escreve \(\mtblank x\mtblank\) na última fita, enumerando \(x\). Por outro lado, para toda palavra \(x\notin L\) e todo \(j\), a emulação de \(M\) para \(x\) por no máximo \(j\) passos nunca atinge estado final, e \(\mtblank x\mtblank\) nunca é escrito na última fita durante a execução de \(E_L\) para \(\upeps\).

(Necessidade) Se existe uma Máquina \(E_L=(Q,\Sigma,\delta,q_0,\qyes,\qno)\) que enumera \(L\), podemos construir uma Máquina de Turing \(M\) que aceita \(L\), conforme pseudocódigo a seguir, em que adicionamos à Máquina \(M\) um estado especial de não-parada \(q_{\mtup}\), como na demonstração do Teorema 6.9.

\(\underline{M(x)}\):

1. acompanhe a emulação de \(E_L\) para \(\upeps\) e, se nalgum momento \(E_L\) escrever \(\mtblank x\mtblank\) na fita, aborte a emulação e devolva \(\mtyes\);
2. entre em \(q_{\mtup}\).

Se \(x\in L\), então, nalgum momento a computação de \(E_L\) para \(\upeps\) enumera \(x\), e temos \(M(x)=\mtyes\). Por outro lado, se \(x\notin L\), independentemente de a computação de \(E_L\) para \(\upeps\) parar ou não, \(M\) nunca para para \(x\). □

LEMA 6.20. Para toda linguagem recursivamente enumerável não-vazia \(L\subseteq\Sigma^{\ast}\) existe uma função recursiva \(f\colon \Sigma^{\ast} \to\Sigma^{\ast}\) cuja imagem é exatamente \(L\).

Demonstração. Seja \(L\subseteq\Sigma^{\ast}\) uma linguagem recursivamente enumerável não-vazia. Temos, do Teorema 6.19, que existe uma Máquina de Turing \(M\) com alfabeto \(\Sigma\) que satisfaz \(E(M)=L\). Construamos, então, uma Máquina de Turing \(W\) de múltiplas fitas com alfabeto \(\Sigma\) que possua uma fita de entrada (a primeira) e uma fita de saída (a última) reservadas, usando suas demais fitas para emular (parcialmente ou tantas vezes quantas necessárias) a computação de \(M\) para \(\upeps\), conforme o pseudocódigo a seguir.

\(\underline{W(x)}\):

1. prepare-se para iniciar a emulação da Máquina \(M\) para a entrada \(\upeps\);
2. repita indefinidamente:
3. \(\quad\) prossiga com a emulação de \(M\) até \(M\) enumerar uma palavra \(y\), reiniciando a emulação para \(\upeps\) caso a emulação atinja estado final sem enumerar palavra alguma;
4. \(\quad\) \(z\leftarrow y\);
5. \(\quad\) se \(x=\upeps\), devolva \(z\).
6. \(\quad\) decremente \(x\) na 1ª fita segundo a ordem lexicográfica de \(\Sigma^{\ast}\);

Por causa das linhas 5 e 6, é claro que \(W\) para para toda entrada \(x\). Seja, portanto, \(f\) a função recursiva que \(W\) computa. Notemos que, para toda palavra \(x\in \Sigma^{\ast}\), temos que \(f(x)=W(x)\) é uma palavra \(y\) enumerada nalgum momento da computação de \(M\) para \(\upeps\), o que nos traz que \(f(x)\in L\) e, consequentemente, que \(f(\Sigma^{\ast})\subseteq L\).

Para mostrarmos que \(L\subseteq f(\Sigma^{\ast})\), percebamos que, para toda palavra \(y\in L\) existe um inteiro \(i \geq 1\) tal que \(y\) é a \(i\)-ésima palavra enumerada na computação de \(M\) para \(\upeps\). Logo, tomando-se \(x\) a \(i\)-ésima palavra na ordem lexicográfica de \(\Sigma^{\ast}\), temos que \(W(x)=y=f(x)\), como queríamos. □

LEMA 6.21. Se existe uma redução \(R\) de uma linguagem \(L_1\) a uma linguagem \(L_2\) e se \(L_1\) não é uma linguagem recursivamente enumerável, então \(L_2\) também não é recursivamente enumerável.

Demonstração. Por contraposição, suponhamos que \(L_2\) seja recursivamente enumerável, i.e. que exista uma Máquina de Turing \(M\) que aceita \(L_2\). Para mostrarmos que \(L_1\) também é recursivamente enumerável, basta tomarmos a mesma Máquina de Turing \(M'\) construída na demonstração do Lema 6.11. Se \(x\in L_1\), então \(R(x)\in L_2\) e, portanto, \(M'(x)=M(R(x))=\mtyes\). Se \(x\notin L_1\), então \(R(x)\notin L_2\) e, portanto, \(M'(x)=M(R(x))=\mtup\). Portanto, \(M'\) aceita \(L_1\). □

TEOREMA 6.22. \({\mathrm{HALTING}_T}\notin\mathsf{RE}\cup\mathsf{coRE}\).

Demonstração. Vamos primeiro mostrar que \({\mathrm{HALTING}_T}\notin\mathsf{RE}\). Supondo a fim de contradição que \({\mathrm{HALTING}_T}\in\mathsf{RE}\), temos, do Lema 6.20 que existe uma função recursiva \({f}\colon{\Sigma_U^{\ast}}\to{\Sigma_U^{\ast}}\) cuja imagem é \({\mathrm{HALTING}_T}\). Seja \(W\) uma Máquina de Turing que computa \(f\). Construamos, então, a Máquina de Turing \(D\) com alfabeto \(\Sigma_U\) conforme o pseudocódigo a seguir.

\(\underline{D(x)}\):

1. emule a Máquina \(W\) para \(x\) e assim obtenha \(\langle{M}\rangle\leftarrow W(x)\);
2. emule \(M\) para \(x\);
3. se \(M(x)=\mtno\), devolva \(\mtyes\);
4. devolva \(\mtno\).

Uma vez que para toda entrada \(x\) a Máquina \(W\) para, e uma vez que \(W(x)\) é a codificação de uma Máquina \(M\) que para para toda entrada, inclusive \(x\), a máquina \(D\) para para toda entrada, do que inferimos que \(\langle D\rangle\in\mathrm{HALTING}_T\). Logo, precisa haver algum \(x_D\in\Sigma_U^{\ast}\) tal que \(f(x_D)=\langle D\rangle\). Quando \(D\) recebe \(x_D\), a Máquina \(M\) obtida na linha 1 é a própria Máquina \(D\). Analisemos se \(D\) aceita \(x_D\):

• se \(D\) aceita \(x_D\), então, a emulação da Máquina \(D\) na linha 2 para \(x_D\) não devolve \(\mtno\), o que faz \(D\) devolver \(\mtno\), uma contradição;
• se \(D\) rejeita \(x_D\), então, a emulação da Máquina \(D\) na linha 2 para \(x_D\) devolve \(\mtno\), o que faz \(D\) devolver \(\mtyes\), também uma contradição.

Como nos dois únicos casos possíveis chegamos a uma contradição, concluímos que a função \(f\) não pode existir. Logo, \(\mathrm{HALTING}_T\) não pode ser recursivamente enumerável.

Agora, vamos mostrar que \(\overline{\mathrm{HALTING}_T}\notin\mathsf{RE}\), exibindo uma redução de \(\overline{\mathrm{HALTING}}\) em \(\overline{\mathrm{HALTING}_T}\), conforme o Lema 6.21 (recorde-se do Corolário 6.17 que \(\overline{\mathrm{HALTING}}\notin\mathsf{RE}\)). Para tanto, basta tomar a mesma redução \(R\) construída na demonstração do Teorema 6.12, pois:

• se \(\langle M\rangle{;}x\in\overline{\mathrm{HALTING}}\), então \(M'\bydef R(\langle M\rangle{;}x)\) é uma Máquina para a qual existe uma entrada (\(x\), no caso) para a qual \(M'\) não para, do que segue que \(M'\in\overline{\mathrm{HALTING}_T}\);
• se \(\langle M\rangle{;}x\notin\overline{\mathrm{HALTING}}\), então \(M'\bydef R(\langle M\rangle{;}x)\) é uma Máquina que para para toda entrada, inclusive \(x\), do que segue que \(M'\notin\overline{\mathrm{HALTING}_T}\). □

• Base: [Pap93] Cap. 2

A seguir, por simplicidade, a funções de codificação denotadas por \(\langle\rangle_{\mu}\) podemos nos referir apenas por \(\mu\).

DEFINIÇÃO B.1. Sendo \(\Sigma\) um alfabeto, \(x\in\Sigma^{\ast}\), e \(\mu\) uma função de codificação de máquinas de Turing com alfabeto \(\Sigma\), a complexidade de Kolmogorov de \(x\) com relação a \(\mu\) é o valor

\begin{equation*} K_{\mu}(x)\bydef \min\{\lvert \langle M \rangle_{\mu}\rvert\mathbin : M(\upeps)=x\}\,. \end{equation*}

TEOREMA B.2. Seja \(\Sigma\) um alfabeto. Existe uma função de codificação \(\mu_0\) tal que, para toda função de codificação \(\mu\), existe uma constante positiva \(c\) tal que, para todo \(x\in\Sigma^{\ast}\),

\begin{equation*} K_{\mu_0}(x)\leq K_{\mu}(x) + c\,. \end{equation*}

Demonstração. Para um esquema de codificação \(\mu\) qualquer, seja \(I_{\mu}\) o interpretador que transforma codificações sob \(\mu\) em codificações para a Máquina Universal \(U\), i.e. \(I_{\mu}\) é a Máquina de Turing tal que, para toda Máquina de Turing \(M\),

\begin{equation*} I_{\mu}(\langle M\rangle_{\mu}) = \langle M\rangle_{U}\,. \end{equation*}

Desta forma, seja \(\mu_0\) o esquema de codificação tal que, para uma Máquina de Turing \(M\) qualquer, sendo \(\mu_M\) o esquema de codificação que minimiza o comprimento total da palavra \(\langle I_{\mu_M}\rangle_U{;}\langle M\rangle_{\mu_M}\),

\begin{equation*} \mu_0(M)\bydef \langle I_{\mu_M}\rangle_U{;}\langle M\rangle_{\mu_M}\,. \end{equation*}

Assim, para qualquer esquema de codificação \(\mu\) e qualquer \(x\in\Sigma^{\ast}\), sendo \(W\) a Máquina de Turing tal que \(W(\upeps)=x\) e \(\langle W\rangle_{\mu}=K_{\mu}(x)\),

\begin{align*} K_{\mu_0}(x)&\leq \lvert\langle W\rangle_{\mu_0}\rvert\\ &= \lvert\langle I_{\mu_W}\rangle_U{;}\langle W\rangle_{\mu_W}\rvert\\ &\leq \lvert\langle I_{\mu}\rangle_U{;}\langle W\rangle_{\mu}\rvert\\ &=K_{\mu}(x) + \lvert\langle I_{\mu}\rangle_U\rvert\,, \end{align*}

e o teorema segue observando-se que \(\lvert\langle I_{\mu}\rangle_U\rvert\) é uma constante que depende apenas de \(\mu\). □

COROLÁRIO B.3. Seja \(\Sigma\) um alfabeto. Existem uma função de codificação \(\mu_0\) e uma constante positiva \(c\) tal que, para todo \(x\in\Sigma^{\ast}\),

\begin{equation*} K_{\mu_0}(x)\leq \lvert x\rvert + c\,. \end{equation*}

Demonstração. Basta tomar para o Teorema B.2 a função de codificação \(\mu\) que, para todo \(x\in\Sigma^{\ast}\), satisfaz \(K_{\mu}(x)=\lvert x\rvert\). Esta função existe, pois basta que, para todo \(x\in\Sigma^{\ast}\), escolhamos uma máquina \(M_x\) tal que \(M_x(\upeps)=x\) e definamos

\begin{equation*} \langle M\rangle_{\mu} \bydef \left\{ \begin{aligned} & M(\upeps)&& \text{se $M$ para para $\upeps$ e $M_{M(\upeps)}=M$;}\\ & \langle M\rangle_{U}{;}M(\upeps)&& \text{se $M$ para para $\upeps$ e $M_{M(\upeps)}\neq M$;}\\ & \langle M\rangle_{U}&& \text{se $M$ não para para $\upeps$.} \end{aligned} \right. \end{equation*}

Observe-se que a definição de \(\mu\) garante que:

• se \(M\) para para \(\upeps\) e \(M_{M(\upeps)}=M\), então, sendo \(x=M(\upeps)\), temos \(\lvert\langle M\rangle_{\mu}\rvert =\lvert x\rvert\);
• se \(M\) para para \(\upeps\) e \(M_{M(\upeps)}\neq M\), então, sendo \(x=M(\upeps)\), temos \(\lvert\langle M\rangle_{\mu}\rvert > \lvert x\rvert\). □

Em vista do Corolário B.3, podemos suprimir a função de codificação da notação, escrevendo apenas \(K(x)\).

LEMA B.4. Seja \(\Sigma\) um alfabeto. Para todo inteiro positivo \(n\), existe \(x\in\Sigma^{\ast}\) tal que \(K(x)\geq n\).

Demonstração. Sendo \(N\) um inteiro positivo fixo, o conjunto das Máquinas de Turing cuja codificação tem comprimento no máximo \(N\) é finito, sendo que cada máquina devolve no máximo uma saída para \(\upeps\). Assim, também é finito o número de palavras \(x\in\Sigma^{\ast}\) para as quais \(K(x)\leq N\). Portanto, o teorema segue do fato de que \(\Sigma^{\ast}\) é infinito. □

Como determinar a complexidade de Kolmogorov de uma dada palavra \(x\) é um problema de otimização, o problema de decisão equivalente pode ser enunciado como: Dada uma palavra \(x\) e um inteiro positivo \(N\), vale que \(K(x)\geq N\)?. Seja \(\mathrm{KOLMOGOROV}\) a linguagem associada a este problema de decisão.

TEOREMA B.5. A complexidade de Kolmogorov não é uma função computável.

Demonstração. É suficiente mostrar \(\mathrm{KOLMOGOROV}\) não é decidível. Para tanto, suponhamos, a fim de contradição, que existe uma Máquina de Turing \(M\) que decida \(\mathrm{KOLMOGOROV}\). Para uma constante \(N\), seja \(W_N\) a Máquina de Turing descrita a seguir.

\(\underline{W_N(y)}\):

1. se \(y=\upeps\):
2. \(\quad\) para \(i\) de \(1\) até \(\infty\):
3. \(\quad\)\(\quad\) para todo \(x\in\Sigma^{i}\):
4. \(\quad\)\(\quad\)\(\quad\) se \(M(x, N)=\mtyes\), devolva \(x\).

Ora, para toda constante \(N\), sabemos do Lema B.4 que existe \(x\in\Sigma^{\ast}\) tal que \(K(x)\geq N\). De todas as palavras \(x\) que satisfazem \(K(x)\geq N\), tomemos a primeira que é considerada por \(W_N(\upeps)\), i.e. aquela tal que \(W_N(\upeps)=x\). Logo, para todo esquema de codificação de Máquinas de Turing \(\mu\), \(\lvert\langle W_N\rangle_{\mu}\rvert\geq K(x)\geq N\). No entanto, o tamanho da descrição de \(W_N\) depende apenas de \(N\) e, sob uma função de codificação apropriada \(\mu'\), temos \(\lvert\langle W_N\rangle_{\mu'}\rvert = O(\log N)\), pois basta definir:

\begin{equation*} \langle M\rangle_{\mu'} \bydef \left\{ \begin{aligned} & \langle N\rangle_2 && \text{se $M=W_N$ para algum $N$;}\\ & \langle M\rangle_{U} && \text{caso contrário.} \end{aligned} \right. \end{equation*}

Logo, para \(N\) suficientemente grande, contradizemos \(\lvert\langle W_N\rangle\rvert \geq N\). □

• Base: [ArBa09] Sec. 1.5; [Pap93] Cap. 4, Sec. 7.1, Cap. 9

DEFINIÇÃO 7.1. Sendo \(\funto f{\bN}{\bN}\), definimos \(\mathsf{TIME}(f(n)) \bydef \{L\mathbin :\text{existe uma MTD $M$ que decide $L$ satisfazendo $T_M(n)=O(f(n))$}\}\) e \(\mathsf{NTIME}(f(n)) \bydef \{L\mathbin :\text{existe uma MTN $N$ que decide $L$ satisfazendo $T_N(n)=O(f(n))$}\}\). Em particular, temos:

\begin{align*} \mathsf P &\;\bydef\; \bigcup_{k\in\bN} \mathsf{TIME}(n^k)\,;\\ \mathsf {EXP} &\;\bydef\; \bigcup_{k\in\bN} \mathsf{TIME}(2^{n^k})\,;\\ \mathsf {NP} &\;\bydef\; \bigcup_{k\in\bN} \mathsf{NTIME}(n^k)\,;\\ \mathsf {NEXP} &\;\bydef\; \bigcup_{k\in\bN} \mathsf{NTIME}(2^{n^k})\,. \end{align*}

Às vezes, as classes \(\mathsf{EXP}\) e \(\mathsf{NEXP}\) são referencidas na literatura como \(\mathsf{EXPTIME}\) e \(\mathsf{NEXPTIME}\).

DEFINIÇÃO 7.2. Seja \(M=(k,Q,\Sigma,\delta,q_0,\qyes)\) uma Máquina de Turing, Determinística ou Não-determinística, com \(k\geq 3\) fitas, sendo a primeira fita apenas de leitura, e a última apenas de escrita, i.e. \(\delta\) relaciona tuplas \((q,s_1,s_2,\dotsc,s_{k-1})\) a tuplas \((p,(r_2,m_2),\dotsc,(r_{k-1},m_{k-1}),(r_k,m_k))\). O espaço de \(M\) para uma entrada \(x\in\Sigma^{\ast}\) é denotado e definido por:

\begin{equation*} s_M(x) \bydef \max_{\substack{C=(q,(w_1,u_1),\dotsc,(w_k,u_k))\\ C_0(x)\underset{M}{\overset{\ast}\Rightarrow} C}} \lvert w_2\cdot u_2\cdot\dotsb\cdot w_{k-1}\cdot u_{k-1}\rvert\,. \end{equation*}

A complexidade de espaço de \(M\) para um comprimento de entrada \(n\in\bN\) é:

• uma função \(\funto f{\bN}{\bN}\), e escrevemos \(S_M(n)=f(n)\), se \(s_M(x)=f(n)\) , para toda entrada \(x\) com \(\lvert x\rvert = n\);
• uma classe de funções \(\mathscr C\) de \(\bN\) em \(\bN\), e escrevemos \(S_M(n)=\mathscr C(n)\) (e.g. \(S_M(n)=O(n)\)), se, para toda entrada \(x\) com \(\lvert x\rvert=n\), existe uma função \(f\in\mathscr C\) tal que \(s_M(x)=f(n)\).

DEFINIÇÃO 7.3. Sendo \(\funto f{\bN}{\bN}\), definimos \(\mathsf{SPACE}(f(n)) \bydef \{L\mathbin :\text{existe uma MTD $M$ que decide $L$ satisfazendo $S_M(n)=O(f(n))$}\}\) e \(\mathsf{NSPACE}(f(n)) \bydef \{L\mathbin :\text{existe uma MTN $N$ que decide $L$ satisfazendo $S_N(n)=O(f(n))$}\}\). Em particular, temos:

\begin{align*} \mathsf L &\;\bydef\; \mathsf{SPACE}(\log n)\,;\\ \mathsf {PSPACE} &\;\bydef\; \bigcup_{k\in\bN} \mathsf{SPACE}(n^k)\,;\\ \mathsf {NL} &\;\bydef\; \mathsf{NSPACE}(\log n)\,;\\ \mathsf {NPSPACE} &\;\bydef\; \bigcup_{k\in\bN} \mathsf{NSPACE}(n^k)\,. \end{align*}

TEOREMA 7.4. Sobre as classes de complexidade de tempo e de espaço, valem as relações

\begin{equation*} \mathsf L\subseteq\mathsf{NL}\subseteq \mathsf{P}\subseteq\mathsf{NP} \subseteq\mathsf{PSPACE}=\mathsf{NPSPACE}\subseteq\mathsf{EXP}\subseteq\mathsf{NEXP}\,. \end{equation*}

Em particular, sabemos que \(\mathsf {NL}\neq\mathsf{PSPACE}\), que \(\mathsf P\neq\mathsf{EXP}\), e que \(\mathsf {NP}\neq\mathsf{NEXP}\). No entanto, não se sabe se é própria alguma outra inclusão envolvendo as classes \(\mathsf L,\mathsf{NL}, \mathsf{P},\mathsf{NP}\), ou as classes \(\mathsf{P},\mathsf{NP},\mathsf{PSPACE}\), ou as classes \(\mathsf{PSPACE},\mathsf{EXP},\mathsf{NEXP}\). □

As classes de complexidade de espaço são um dos vários tópicos estudados no curso de Complexidade Computacional (CSA41), ofertado regularmente pelo DAINF/UTFPR-CT. A demonstração de todas as inclusões do Teorema 7.4 é estudada nesse curso.

DEFINIÇÃO 7.5 (Tese de Cobham). Uma linguagem decidível \(L\) é dita tratável se existe uma Máquina de Turing Determinística que decide \(L\) com complexidade de tempo polinomial.

Por abuso, dizemos que um problema de decisão \(P\) está numa classe de complexidade de linguagens \(\mathcal C\) quando a linguagem associada a \(P\) está em \(\mathcal C\). Assim, podemos construir asserções como O Problema da Primalidade está em \(\mathsf P\), ou O Problema da Parada é \(\mathsf{NP}\)-difícil.

DEFINIÇÃO 7.6. Uma linguagem \(L\) é \(\mathsf{NP}\)-difícil se, para toda linguagem \(L'\in\mathsf{NP}\), existe uma redução polinomial \(R\) (i.e. uma redução de complexidade de tempo polinomial) tal que \(L'\prec_R L\). Uma linguagem \(L\) é completa para a classe \(\mathsf{NP}\), ou simplesmente \(\mathsf{NP}\)-completa, se

1. \(L\in\mathsf{NP}\);
2. \(L\) é \(\mathsf{NP}\)-difícil.

TEOREMA 7.7 (Teorema de Cook–Levin). O Problema da Satisfazibilidade Booleana é \(\mathsf{NP}\)-completo.

Antes de apresentarmos a demonstração do Teorema 7.7, precisamos estudar a definição do Problema da Satisfazibilidade Booleana e os conceitos elementares em Lógica Booleana.

DEFINIÇÃO 7.8. Sendo \(\mathbf V\) e \(\mathbf F\) os valores-verdade, e sendo \(n\in\bN\), uma função booleana \(n\)-ária é uma função de \(\{\mathbf V,\mathbf F\}^n\) em \(\{\mathbf V,\mathbf F\}\).

Como exemplo, listamos todas as quatro funções booleanas unárias:

\begin{equation*} \begin{aligned} {f_1}\colon{(\mathbf V)}\mapsto{\mathbf V}&\qquad {f_2}\colon{(\mathbf V)}\mapsto{\mathbf V}& {f_3}\colon{(\mathbf V)}\mapsto{\mathbf F}&\qquad {f_4}\colon{(\mathbf V)}\mapsto{\mathbf F}\\ {f_1}\colon{(\mathbf F)}\mapsto{\mathbf V}&\qquad {f_2}\colon{(\mathbf F)}\mapsto{\mathbf F}& {f_3}\colon{(\mathbf F)}\mapsto{\mathbf V}&\qquad {f_4}\colon{(\mathbf F)}\mapsto{\mathbf F} \end{aligned} \end{equation*}

DEFINIÇÃO 7.9 (Expressão booleana; Fórmula booleana). Seja \(n\in\bN\) e \(X=\{x_1,x_2,\dotsc,x_n\}\) um conjunto de \(n\) variáveis booleanas.

1. Para todo \(x_i\in X\), as expressões \(x_i\) e \(\neg x_i\) são expressões booleanas (ou fórmulas booleanas) sobre \(X\), neste caso chamadas de literais. Expressões da forma \(x_i\) são chamadas de literais positivos e têm comprimento \(\lvert x_i\rvert\bydef 1\), enquanto que expressões da forma \(\neg x_i\) são chamadas de literais negativos e têm comprimento \(\lvert \neg x_i\rvert\bydef 2\).
2. Se \(\phi\) é uma expressão booleana sobre \(X\), então \(\neg\phi\) também é, tendo comprimento \(\lvert\neg\phi\rvert\bydef =1+\lvert\phi\rvert\).
3. Se \(\phi_1\) e \(\phi_2\) são expressões booleanas sobre \(X\), então \(\phi_1\wedge \phi_2\) também é, tendo comprimento \(\lvert\phi_1\wedge \phi_2\rvert = \lvert\phi_1\rvert+1+\lvert \phi_2\rvert\).
4. Se \(\phi_1\) e \(\phi_2\) são expressões booleanas sobre \(X\), então \(\phi_1\vee \phi_2\) também é, tendo comprimento \(\lvert\phi_1\vee \phi_2\rvert = \lvert\phi_1\rvert+1+\lvert \phi_2\rvert\).

Em expressões booleanas, convencionamos que o operador de negação (\(\neg\)) tem precedência sobre os operadores de conjunção (\(\wedge\)) e disjunção (\(\vee\)), porém não estabelecemos precedência entre estes dois últimos. Naturalmente, a precedência dos operadores booleanos pode ser alterada através do uso de parênteses.

Um exemplo de expressão booleana sobre \(X=\{x_1,x_2,x_3,x_4\}\) é:

\begin{equation} \phi\colon (x_1\wedge x_2\wedge x_4)\vee (\neg x_1\wedge(\neg x_3\vee(x_2\wedge x_3\wedge x_4)))\,. \end{equation}

DEFINIÇÃO 7.10. Seja \(n\in\bN\) e \(X=\{x_1,x_2,\dotsc,x_n\}\) um conjunto de \(n\) variáveis booleanas. Uma valoração de \(X\) é uma função \(T\colon X\to \{\mathbf V,\mathbf F\}\).

DEFINIÇÃO 7.11. Dizemos que uma valoração \(T\) de um conjunto de variáveis booleanas \(X\) satisfaz uma expressão booleana \(\phi\) sobre \(X\), e escrevemos \(T\models\phi\), se ocorre um dos seguintes casos:

1. \(\phi\) é um literal positivo \(x_i\) sobre \(X\) e \(T(x_i)=\mathbf V\), ou \(\phi\) é um literal negativo \(\neg x_i\) sobre \(X\) e \(T(x_i)=\mathbf F\);
2. \(\phi\) é uma expressão booleana da forma \(\neg\psi\) e \(T\not\models\psi\);
3. \(\phi\) é uma expressão booleana da forma \(\psi_1\wedge\psi_2\) e ocorrem tanto \(T\models\psi_1\) quanto \(T\models\psi_2\);
4. \(\phi\) é uma expressão booleana da forma \(\psi_1\vee\psi_2\) e ocorre \(T\models\psi_1\) ou \(T\models\psi_2\).

DEFINIÇÃO 7.12. Dizemos que uma expressão booleana \(\phi\) sobre um conjunto ordenado de variáveis \(X=\{x_1,\dotsc,x_n\}\) representa uma função booleana \(n\)-ária \(f\) quando, para toda valoração \(T\) de \(X\), vale que:

\begin{equation*} T\models\phi\quad\text{se e somente se}\quad f(T(x_1),T(x_2),\dotsc,T(x_n))=\mathbf V\,. \end{equation*}

TEOREMA 7.13. Toda função booleana \(n\)-ária pode ser representada por uma expressão booleana \(\phi\) sobre \(X=\{x_1,\dotsc,x_n\}\) de comprimento \(O(n2^n)\).

Demonstração. Sejam \(n\in\bN\) e \(f\) uma função booleana \(n\)-ária. Se \(f(t_1,\dotsc,t_n)=\mathbf F\) para todo \((t_1,\dotsc,t_n)\in\{\mathbf V,\mathbf F\}^n\), então, a expressão booleana \(x_1\wedge\neg x_1\) representa \(f\). Suponhamos, então, que \(f^{-1}(\mathbf V)\neq\emptyset\), e definamos, para cada \(n\)-tupla \(\boldsymbol t=(t_1,\dotsc,t_n)\) tal que \(f(\boldsymbol t)=\mathbf V\), a expressão booleana

\begin{equation*} D_{\boldsymbol t}\colon \bigwedge_{j=1}^n \ell_j\,, \end{equation*}

sendo \(\ell_j\) o literal \(x_j\), se \(t_j=\mathbf V\), ou o literal \(\neg x_j\), se \(t_j=\mathbf F\). Vamos mostrar que a expressão booleana

\begin{equation*} \phi\colon \bigvee_{\boldsymbol t\in f^{-1}(\mathbf V)}D_{\boldsymbol t} \end{equation*}

representa \(f\).

• Se uma valoração \(T\) de \(X\) satisfaz \(\phi\), então, há ao menos uma expressão \(D_{\boldsymbol t}\) tal que \(T\models D_{\boldsymbol t}\). Para \(T\) satisfazer \(D_{\boldsymbol t}\), precisa satisfazer todos os literais de \(D_{\boldsymbol t}\). Então, sendo \(\boldsymbol t=(t_1,\dotsc,t_n)\), temos \(T(x_i)=t_i\) para todo \(x_i\in X\). Logo, \(f(T(x_1),\dotsc,T(x_n))=\mathbf V\).
• Se \(f(t_1,\dotsc,t_n)=\mathbf V\), então, tomando-se a valoração \(T\) definida por \(T(x_i)\bydef t_i\), e tomando-se \(\boldsymbol t\bydef(t_1,\dotsc,t_n)\), temos que \(T\) satisfaz \(D_{\boldsymbol t}\) e, portanto, que satisfaz \(\phi\).

Por fim, vamos mostrar que o comprimento de \(\phi\) é \(O(n2^n)\). Para todo \(\boldsymbol t\in f^{-1}(\mathbf V)\),

\begin{equation*} \lvert{D_{\boldsymbol t}}\rvert=\biggl\lvert{\bigwedge_{j=1}^n \ell_j}\biggr\rvert= {\biggl(\sum_{j=1}^n \lvert{\ell_j}\rvert\biggr) + (n-1)}\leq {\biggl(\sum_{j=1}^n 2\biggr) + n}=3n\,, \end{equation*}

já que o comprimento de todo literal \(\ell_j\) é no máximo 2. Assim,

\begin{equation*} \lvert{\phi}\rvert =\biggl\lvert{\bigvee_{\boldsymbol t\in f^{-1}(\mathbf V)}D_{\boldsymbol t}}\biggr\rvert =\biggl(\sum_{\boldsymbol t\in f^{-1}(\mathbf V)}\lvert{D_{\boldsymbol t}}\rvert\biggr) +(\lvert{f^{-1}(\mathbf V)}\rvert-1) \leq \lvert{f^{-1}(\mathbf V)}\rvert(3n+1)\,. \end{equation*}

Como \(f^{-1}(\mathbf V)\subseteq\{\mathbf V,\mathbf F\}^n\), temos que \(\lvert{f^{-1}(\mathbf V)}\rvert\leq2^n\), o que nos traz que \(\lvert{\phi}\rvert\leq2^n(3n+1)\). □

Apesar de o comprimento \(O(n2^n)\) das expressões booleanas do Teorema 7.13, existem funções booleanas que podem ser representadas por expressões booleanas menores, de comprimento até polinomial. No entanto, há funções booleanas que necessariamente só podem ser representadas por expressões de comprimento exponencial. Na verdade, como veremos no Teorema 7.17, há funções booleanas que necessariamente só podem ser computadas por circuitos booleanos de tamanho exponencial, mesmo circuitos booleanos serem geralmente uma forma mais compacta de se representarem funções booleanas.

DEFINIÇÃO 7.14. Seja \(n\in\bN\) e \(X=\{x_1,x_2,\dotsc,x_n\}\) um conjunto de \(n\) variáveis booleanas. Um circuito booleano sobre \(X\) é um grafo dirigido acíclico \(C\) munido de uma função \(s\colon {V(C)}\to{X\cup\{\mathbf V,\mathbf F,\neg,\wedge,\vee\}}\) de rotulação dos vértices tal que:

1. os vértices de \(C\) são chamados de portas;
2. para toda porta \(u\), temos \(d^-_C(u)\in\{0,1,2\}\);
3. há exatamente uma porta \(u\) com \(d^+_C(u)=0\), a qual é denominada a porta de saída do circuito \(C\);
4. se \(d^-_C(u)=0\), então \(u\) é dita uma porta de entrada de \(C\), e \(s(u)\in X\cup\{\mathbf V,\mathbf F\}\);
5. se \(d^-_C(u)=1\), então, \(s(u)=\neg\);
6. se \(d^-_C(u)=2\), então, \(s(u)\in\{\wedge,\vee\}\).

Ainda, o tamanho do circuito \(C\), denotado por \(\lvert C\rvert\), é o número de portas de \(C\), enquanto a profundidade de \(C\) é o maior número de arestas no caminho de uma porta de entrada à porta de saída de \(C\).

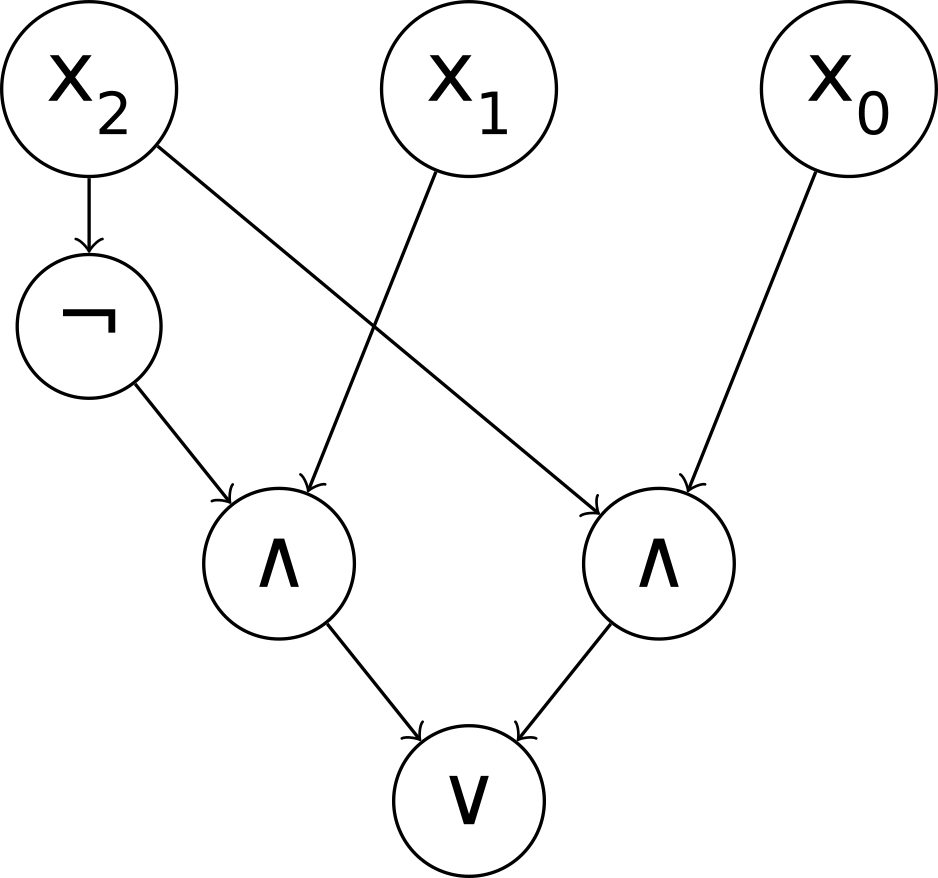
DEFINIÇÃO 7.15. Seja \(X=\{x_1,x_2,\dotsc,x_n\}\), seja \(C\) um circuito booleano sobre \(X\), e seja \(T\) uma valoração de \(X\). A valoração de \(C\) induzida por \(T\) é a função \(T\colon V(C)\to\{\mathbf V,\mathbf F\}\) tal que:

1. para toda porta de entrada \(u\) rotulada com algum \(x_i\in X\), temos \(T(u)=T(x_i)\);
2. para toda porta de entrada \(u\) tal que \(s(u)\in\{\mathbf V,\mathbf F\}\), temos \(T(u)=s(u)\);
3. para toda porta \(u\) com \(s(u)=\neg\), sendo \(v\) a única porta de \(C\) tal que \(vu\in E(C)\), temos \(T(u)=\neg T(v)\);
4. para toda porta \(u\) com \(s(u)=\wedge\), sendo \(v_1\) e \(v_2\) as únicas portas de \(C\) tais que \(v_1u,v_2u\in E(C)\), temos \(T(u)= T(v_1)\wedge T(v_2)\);
5. para toda porta \(u\) com \(s(u)=\wedge\), sendo \(v_1\) e \(v_2\) as únicas portas de \(C\) tais que \(v_1u,v_2u\in E(C)\), temos \(T(u)= T(v_1)\wedge T(v_2)\).

Ainda, o valor de \(C\) para \(T\), denotado por \(T(C)\), é o valor \(T(u)\) para a única porta de saída \(u\) de \(C\). Dizemos que \(T\) satisfaz \(C\), e escrevemos \(T\models C\), se e somente se \(T(C)=\mathbf V\).

DEFINIÇÃO 7.16. Dizemos que um circuito booleano \(C\) sobre um conjunto ordenado de variáveis \(X=\{x_1,\dotsc,x_n\}\) computa uma função booleana \(n\)-ária \(f\) quando, para toda valoração \(T\) de \(X\), vale que:

\begin{equation*} T\models C\quad\text{se e somente se}\quad f(T(x_1),T(x_2),\dotsc,T(x_n))=\mathbf V\,. \end{equation*}

TEOREMA 7.17. Para todo \(n\geq2\), existe uma função booleana \(n\)-ária \(f\) tal que \(f\) não pode ser computada por um circuito booleano com \({2^n}/{2n}\) portas ou menos.

Demonstração. Primeiramente, vamos mostrar que, para quaisquer \(n,m\in\bZ_{> 0}\), o número de circuitos booleanos com no máximo \(m\) portas e no máximo \(n\) variáveis é não maior que \(((n+5)m^2)^m\). Seja \(C\) um circuito com no máximo \(m\) portas e no máximo \(n\) variáveis. Cada porta pode ter um dos no máximo \(n+5\) rótulos possíveis (\(x_1,\dotsc,x_n,\mathbf V,\mathbf F,\neg,\wedge,\vee\)) e receber como entrada no máximo duas das \(m\) portas do circuito, o que resulta em no máximo \((n+5)m^2\) possíveis diferentes configurações para cada porta. Como são \(m\) portas, temos um total de circuitos possíveis não maior que \(((n+5)m^2)^m\).

Tomemos \(n\geq2\). Seja, então, \(n_1\) o número de funções booleanas \(n\)-árias, e seja \(n_2\) o número de circuitos booleanos com no máximo \({2^n}/{2n}\) portas e no máximo \(n\) variáveis. Sabemos que

\begin{align*} n_1&=2^{2^n}\qquad\text{e}\\ n_2&\leq \Bigl( (n+5)\Bigl(\frac{2^n}{2n}\Bigr)^2 \Bigr)^{\frac{2^n}{2n}}\,. \end{align*}

Ora,

\begin{align*} \lg n_2&\leq \lg\Bigl( (n+5)\Bigl(\frac{2^n}{2n}\Bigr)^2 \Bigr)^{\frac{2^n}{2n}}\\ &={\frac{2^n}{2n}}\lg\Bigl( (n+5)\Bigl(\frac{2^n}{2n}\Bigr)^2 \Bigr)\\ &={\frac{2^n}{2n}}\Bigl( \lg(n+5)+\lg\Bigl(\frac{2^n}{2n}\Bigr)^2 \Bigr)\\ &={\frac{2^n}{2n}}\Bigl( \lg(n+5)+2\lg\Bigl(\frac{2^n}{2n}\Bigr) \Bigr)\\ &={\frac{2^n}{2n}}\bigl( \lg(n+5)+2(\lg{2^n}-\lg{2n}) \bigr)\\ &={\frac{2^n}{2n}}\bigl( \lg(n+5)+2(n-\lg n-\lg2) \bigr)\\ &={\frac{2^n}{2n}}\bigl( \lg(n+5)+2n-2\lg n-2 \bigr)\\ &={\frac{2^n}{2n}}\bigl( 2n-(2\lg n+2- \lg(n+5) ) \bigr)\\ &=2^n\Bigl( 1-\Bigl( \frac{\lg n+1-\frac12\lg(n+5)}n \Bigr) \Bigr)<2^n=\lg n_1\,, \end{align*}

pois \(n\geq 2\). Portanto, \(n_2 < n_1\), o que significa que há mais funções booleanas \(n\)-árias que circuitos booleanos com no máximo \({2^n}/{2n}\) portas. Logo, há pelo menos uma função booleana que não pode ser computada por um circuito booleano com \({2^n}/{2n}\) ou menos portas. □

DEFINIÇÃO 7.18. Dizemos que uma expressão booleana \(\phi\) está na forma normal conjuntiva (CNF) se \(\phi\) é uma conjunção de cláusulas, sendo cada cláusula uma disjunção de literais.

DEFINIÇÃO 7.19. Dizemos que uma expressão booleana \(\phi\) é satisfazível se existe alguma valoração das variáveis de \(\phi\) que satisfaz \(\phi\).

DEFINIÇÃO 7.20. Dizemos que um circuito booleano \(C\) é satisfazível se existe alguma valoração das variáveis de \(C\) que satisfaz \(C\).

O Problema da Satisfazibilidade Booleana é o problema de decisão definido por: Dada uma expressão booleana \(\phi\) na CNF, \(\phi\) é satisfazível? A linguagem associada a este problema é denotada por \(\mathrm{SAT}\).

O Problema da Satisfazibilidade de Circuitos Booleanos é o problema de decisão definido por: Dado um circuito booleano \(C\), o circuito \(C\) é satisfazível? A linguagem associada a este problema é denotada por \(\mathrm{CIRCUIT\,SAT}\).

LEMA 7.21. \(\mathrm{SAT}\) e \(\mathrm{CIRCUIT\,SAT}\) estão em \(\mathsf{NP}\).

Demonstração. Vamos primeiro mostrar que o algoritmo não-determinístico \(\text{NSatSolver}\), descrito no pseudocódigo a seguir, decide \(\mathrm{SAT}\) em tempo polinomial.

\(\underline{\text{NSatSolver}(\varphi)}\):

1. para toda variável \(x\) de \(\varphi\), faça:
2. \(\quad\) adivinhe um valor-verdade para \(T(x)\);
3. para toda cláusula \(D\) de \(\varphi\), faça:
4. \(\quad\) \(flag\leftarrow\mathbf F\);
5. \(\quad\) para todo literal \(\ell\) de \(D\), faça:
6. \(\quad\)\(\quad\) se \(T\models \ell\), então \(flag\leftarrow\mathbf V\);
7. \(\quad\) se \(flag=\mathbf F\), então devolva \(\mtno\);
8. devolva \(\mtyes\).

Por construção, cada computação possível de \(\text{NSatSolver}\) para uma entrada \(\varphi\) qualquer tem complexidade de tempo linear em \(\lvert\varphi\rvert\), pois adivinha uma dentre todas as valorações possíveis para as variáveis de \(\varphi\), e depois realiza uma única varredura sobre \(\varphi\), para testar se a valoração escolhida satisfaz \(\varphi\). Portanto, se existe alguma valoração \(T\) que satisfaz \(\varphi\), então alguma computação constrói essa valoração nas linhas 1–2, e essa computação devolve \(\mtyes\). Por outro lado, se nenhuma valoração \(T\) satisfaz \(\varphi\), então toda computação devolve \(\mtno\).

Vamos agora mostrar que o algoritmo não-determinístico \(\text{NCircuitSatSolver}\), descrito no pseudocódigo a seguir, decide \(\mathrm{CIRCUIT\,SAT}\) em tempo polinomial.

\(\underline{\text{NCircuitSatSolver}(C)}\):

1. para toda variável \(x\) de \(C\), faça:
2. \(\quad\) adivinhe um valor-verdade para \(T(x)\);
3. tome uma ordenação topológica \(g_1,g_2,\dotsc,g_{n}\) das portas de \(C\), sendo \(g_n\) a porta de saída de \(C\);
4. para \(i\) de \(1\) até \(n\), faça:
5. \(\quad\) se \(s(g_i)\in\{\mathbf V,\mathbf F\}\), então \(T(g_i)\leftarrow s(g_i)\);
6. \(\quad\) se \(s(g_i)\) é uma variável \(x\), então \(T(g_i)\leftarrow T(x)\);
7. \(\quad\) se \(s(g_i)=\wedge\), sendo \(g_{j}\) e \(g_{k}\) as portas que servem \(g_i\), então \(T(g_i)\leftarrow T(g_j)\wedge T(g_k)\);
8. \(\quad\) se \(s(g_i)=\vee\), sendo \(g_{j}\) e \(g_{k}\) as portas que servem \(g_i\), então \(T(g_i)\leftarrow T(g_j)\vee T(g_k)\);
9. se \(T(g_n)=\mathbf V\), devolva \(\mtyes\).
10. devolva \(\mtno\).

Por construção, cada computação possível de \(\text{NCircuitSatSolver}\) para uma entrada \(C\) qualquer tem complexidade de tempo linear no número de portas de \(C\), pois adivinha uma dentre todas as valorações possíveis para as variáveis de \(C\), e depois realiza uma única varredura sobre \(C\), segundo uma ordem topológica das portas, para testar se a valoração escolhida satisfaz \(C\). Portanto, se existe alguma valoração \(T\) que satisfaz \(C\), então alguma computação constrói essa valoração nas linhas 1–2, e essa computação devolve \(\mtyes\). Por outro lado, se nenhuma valoração \(T\) satisfaz \(C\), então toda computação devolve \(\mtno\). □

LEMA 7.22. Existe uma redução polinomial \(R\) tal que \(\mathrm{CIRCUIT\,SAT}\prec_R \mathrm{SAT}\).

Demonstração. Vamos construir uma redução \(R\) que, ao receber um circuito booleano \(C\) e, devolve uma expressão booleana \(\def\fedyb{\mathbin{=:}}R(C)\fedyb\phi\) na CNF, de modo que \(\phi\) é satisfazível se e só se \(C\) também o é. Para tanto, sendo \(X\) o conjunto das variáveis de \(C\), a redução \(R\) inicializa uma expressão booleana vazia \(\phi\) sobre o conjunto de variáveis \(X\cup V(C)\), i.e. o conjunto das variáveis de \(\phi\) será o conjunto das variáveis de \(C\) e o conjunto das portas de \(C\), supondo sem perda de generalidade que \(X\) e \(V(C)\) são disjuntos. Em seguida, \(R\) faz uma varredura sobre \(C\) e, a cada porta \(u\) lida:

• se \(u\) for uma porta de entrada tal que \(s(u)=\mathbf V\), então \(R\) adiciona a cláusula \((u)\) a \(\phi\), pois, assim, toda valoração que satisfizer \(\phi\) obrigatoriamente atribuirá \(\mathbf V\) a \(u\);
• se \(u\) for uma porta de entrada tal que \(s(u)=\mathbf F\), então \(R\) adiciona a cláusula \((\neg u)\) a \(\phi\), pois, assim, toda valoração que satisfizer \(\phi\) obrigatoriamente atribuirá \(\mathbf F\) a \(u\);
• se \(u\) for uma porta de entrada tal que \(s(u)=x\) para alguma variável \(x\) de \(C\), a redução \(R\) adiciona as cláusulas a \(\phi\) que, juntas, expressam a equivalência \(u\Leftrightarrow x\), i.e. as cláusulas \((\neg u\vee x)\) e \((u\vee\neg x)\);
• se \(u\) for uma porta tal que \(s(u)=\neg\), sendo \(v\) a porta que serve \(u\), a redução \(R\) adiciona as cláusulas a \(\phi\) que, juntas, expressam a equivalência \(u\Leftrightarrow \neg v\), i.e. as cláusulas \((\neg u\vee\neg v)\) e \((u\vee v)\);
• se \(u\) for uma porta tal que \(s(u)=\vee\), sendo \(v_1\) e \(v_2\) as portas que servem \(u\), a redução \(R\) adiciona as cláusulas a \(\phi\) que, juntas, expressam a equivalência \(u\Leftrightarrow v_1\vee v_2\), i.e. as cláusulas \((\neg u\vee v_1\vee v_2)\), \((u\vee\neg v_1)\), e \((u\vee\neg v_2)\);
• se \(u\) for uma porta tal que \(s(u)=\wedge\), sendo \(v_1\) e \(v_2\) as portas que servem \(u\), a redução \(R\) adiciona as cláusulas a \(\phi\) que, juntas, expressam a equivalência \(u\Leftrightarrow v_1\wedge v_2\), i.e. as cláusulas \((\neg u\vee v_1)\), \((\neg u\vee v_2)\), e \((u\vee\neg v_1\vee\neg v_2)\);
• se \(u\) for a porta de saída de \(C\), então, \(R\) adiciona a cláusula \((u)\) a \(\phi\), assim, toda valoração que satisfizer \(\phi\) vai obrigatoriamente valorar \(u\) com \(\mathbf V\).

Por construção, se existe uma valoração \(T\) que satisfaz \(C\), então a valoração de \(X\cup V(C)\) definida por \(T\) e pela valoração de \(C\) induzida por \(T\) satisfaz \(\varphi\). Por outro lado, se \(T\) é uma valoração de \(X\cup V(C)\) que satisfaz \(\varphi\), então \(T\) satisfaz \(C\). Ainda, como a redução \(R\) faz uma única varredura sobre \(C\), adicionando a \(\varphi\) um número \(O(1)\) de cláusulas de tamanho \(O(1)\) a cada porta de \(C\) considerada, \(R\) é polinomial. □

Demonstração do Teorema 7.7 (Teorema de Cook–Levin). Já mostramos no Lema 7.21 que ambos \(\mathrm{SAT}\) e \(\mathrm{CIRCUIT\,SAT}\) estão em \(\mathsf{NP}\). Seja \(R'\) a redução de \(\mathrm{CIRCUIT\,SAT}\) para \(\mathsf{SAT}\) construída no Lema 7.22. Vamos mostrar que, para toda linguagem \(L\in\mathsf{NP}\), existe uma redução polinomial \(R\) tal que \(L\prec_R\mathrm{CIRCUIT\,SAT}\), o que implica \(L\prec_{R\circ R'}\mathrm{SAT}\) e, portanto, que ambos \(\mathrm{SAT}\) e \(\mathrm{CIRCUIT\,SAT}\) são \(\mathsf{NP}\)-completos.

Seja \(L\) uma linguagem qualquer de \(\mathsf{NP}\), e seja \(N=(Q,\Sigma,\Delta,q_0,\qyes,\qno)\) uma Máquina de Turing Não-determinística que decide \(L\) para a qual exista um inteiro positivo \(k\) tal que \(T_N(n)\leq n^k\) para todo \(n\geq 2\) (cf. Exercício No description for this link). Suponhamos, sem perda de generalidade, que, para todo \(q\in Q\) e todo \(s\in\Sigma\), temos \(\lvert\Delta(q,s)\rvert=2\) (cf. Exercício No description for this link), sendo as escolhas em \(\Delta(q,s)\) indexadas por \(0\) e \(1\).

Sejam \(x\in\Sigma^{\ast}\) uma entrada para \(N\) e \(c\in\{0,1\}^{\lvert x\rvert^k+1}\) uma sequência \(c_1c_2\dotsb c_{\lvert x\rvert^k+1}\) de \(\lvert x\rvert^k+1\) escolhas que determina uma computação de \(N\) para \(x\), ainda que a computação não use todas as escolhas da sequência. Seja \((\Sigma\cup\{\mtstart,\mtblank\})_Q\bydef\{s_q\mathbin : s\in\Sigma\cup\{\mtstart,\mtblank\},q\in Q\}\). Seja também \(\mathsf T(N,x,c)\) a tábua da computação de \(N\) para \(x\) sob \(c\), i.e. a tabela de \((\lvert x\rvert^k+2)\times(\lvert x\rvert^k+2)\) símbolos de \(\Gamma\bydef (\Sigma\cup\{\mtstart,\mtblank\})\cup (\Sigma\cup\{\mtstart,\mtblank\})_Q\) definida por:

• as linhas e as colunas são indexadas por \(0..\lvert x\rvert^k+1\), de modo que cada linha da tabela corresponde ao conteúdo da fita de \(N\) num instante da computação de \(N\) para \(x\) sob a sequência de escolhas \(c\) (a linha \(0\) corresponde ao instante \(0\), a linha \(1\) ao instante \(1\), e assim por diante);
• em cada linha, apenas uma célula é do tipo \(s_q\) para algum \(s\in\Sigma\cup\{\mtstart,\mtblank\}\) e algum \(q\in Q\), indicando a posição do cabeçote naquele instante;
• a primeira linha, indexada por \(0\), é \(\mtstart\mtstart_{q_0}x\mtblank^{\lvert x\rvert^k-\lvert x\rvert}\);
• quando a computação alcança um estado final no instante \(i<\lvert x\rvert^k+1\), copia-se o conteúdo da linha \(i\) para todas as linhas seguintes;
• como as dimensões da tábua são suficientemente grandes, a primeira célula de cada linha é sempre \(\mtstart\), e a última célula de cada linha é sempre \(\mtblank\).

Observe-se que a célula \(\mathsf T_{ij}\), para \(0 < i\leq\lvert x\rvert^k+1\) e \(0 < j < \lvert x\rvert^k+1\), depende exclusivamente apenas da escolha \(c_i\), e das três células da linha superior: as células \(\mathsf T_{i-1,j-1}\), \(\mathsf T_{i-1,j}\), e \(\mathsf T_{i-1,j+1}\). Isto é, existe uma função \(f\colon {\Gamma^3}\times\{0,1\}\to {\Gamma}\) tal que

\begin{equation*} f(\mathsf T_{i-1,j-1},\mathsf T_{i-1,j},\mathsf T_{i-1,j+1},c_i)={\mathsf T_{ij}}\quad \forall ij, 0 < i\leq\lvert x\rvert^k+1, 0 < j < \lvert x\rvert^k+1\,. \end{equation*}

Observe-se que esta função \(f\) não depende de \(x\), mas exclusivamente de \(N\) (i.e. da relação de transição \(\Delta\)).

Vamos agora transformar \(\mathsf T(N,x,c)\) numa tabela binária \(\mathsf S(N,x,c)\). Para tanto, basta levarmos em consideração que cada símbolo \(\gamma\in\Gamma\) pode ser codificado como uma palavra binária \(\langle \gamma\rangle\) com \(m\bydef \lceil\lg \lvert{\Gamma}\rvert\rceil\) bits. Assim, para obtermos \(\mathsf S(N,x,c)\), trocamos cada célula \(\mathsf T_{ij}\) em \(\mathsf T(N,x,c)\) pelos \(m\) bits que codificam aquela célula: \(\mathsf S_{ij1},\mathsf S_{ij2},\dotsc,\mathsf S_{ijm}\). Logo, para \(1\leq \ell\leq m\), \(0 < i\leq\lvert x\rvert^k+1\), e \(0 < j < \lvert x\rvert^k+1\), cada posição \(\mathsf S_{ij\ell}\), é função de \(\mathsf S_{i-1,j-1,1},\dotsc,\mathsf S_{i-1,j-1,m}\), de \(\mathsf S_{i-1,j,1},\dotsc,\mathsf S_{i-1,j,m}\), de \(\mathsf S_{i-1,j+1,1},\dotsc,\mathsf S_{i-1,j+1,m}\), e de \(c_i\). Então, existem \(m\) funções booleanas \((3m+1)\)-árias \(F_1,\dotsc,F_m\) tais que, para \(1\leq \ell\leq m\), \(0 < i\leq\lvert x\rvert^k+1\), e e \(0 < j < \lvert x\rvert^k+1\),

\begin{equation*} F_\ell(\mathsf S_{i-1,j-1,1},\dotsc,\mathsf S_{i-1,j-1,m}, \mathsf S_{i-1,j,1},\dotsc,\mathsf S_{i-1,j,m}, \mathsf S_{i-1,j+1,1},\dotsc,\mathsf S_{i-1,j+1,m},c_i)= \mathsf S_{ij\ell}\,. \end{equation*}

Observe-se que \(m\) é uma constante que depende exclusivamente de \(N\), assim como as \(m\) funções \(F_1,\dotsc,F_m\) dependem exclusivamente de \(N\). Portanto, existem \(m\) circuitos \(C_1,\dotsc,C_m\) de tamanho \(O(1)\) que computam as funções \(F_1,\dotsc,F_m\), respectivamente.

Apresentaremos agora a redução \(R\), que, ao receber uma palavra \(x\in\Sigma^{\ast}\) como entrada, constrói um circuito \(D\), de modo que \(D\) é satisfazível se e somente se \(x\in L\). O circuito \(D\) é construído por \(R\) juntando-se várias cópias dos circuitos \(C_1,\dotsc,C_m\), sendo cada cópia para cada bit de cada posição da tábua da computação de \(N\) para \(x\) sob uma sequência de escolhas \(c\). Note-se que a redução \(R\) recebe apenas \(x\) como entrada, não a sequência \(c\). Portanto, as portas de entrada do circuito \(D\) correspondentes às escolhas de \(c\) são deixadas como as variáveis de \(D\), enquanto que todas as outras portas de entrada de \(D\) já recebem os valores-verdade correspondentes à codificação de \(x\) ou dos símbolos especiais \(\mtstart\), \(\mtstart_{q_0}\), e \(\mtblank\). As entradas de cada cópia \(C_{\ell}\) referentes ao bit \(\mathsf S_{ij\ell}\), para \(1\leq \ell\leq m\), \(0 < i\leq\lvert x\rvert^k+1\), e e \(0 < j < \lvert x\rvert^k+1\), é alimentada com as saídas das portas correspondentes aos \(3m+1\) bits \(\mathsf S_{i-1,j-1,1},\dotsc,\mathsf S_{i-1,j-1,m},\mathsf S_{i-1,j,1},\dotsc,\mathsf S_{i-1,j,m},\mathsf S_{i-1,j+1,1},\dotsc,\mathsf S_{i-1,j+1,m},c_i\). O circuito \(D\) ainda incorpora um subcircuito \(E\) que testa se o estado final presente na última linha da tábua \(\mathsf T(N,x,c)\) é \(\mtyes\), de modo que a porta de saída do circuito \(D\) é a porta de saída de \(E\). Para construir esse circuito \(E\), basta efetuar, para todo \(\mathsf T_{ij}\) com \(i=\lvert x\rvert^k+1\), a disjunção das saídas de cópias de um circuito \(F\) que testa se os \(m\) bits que codificam \(\mathsf T_{ij}\) coincidem com a codificação do símbolo \(s_{\qyes}\) para algum \(s\in\Sigma\cup\{\mtstart,\mtblank\}\).

Vamos mostrar que a redução funciona.

• Se \(x\in L\), então, existe alguma sequência de escolhas \(c\in\{0,1\}^{\lvert x\rvert^k+1}\) tal que o estado final identificado na última linha de \(\mathsf T(N,x,c)\) é \(\qyes\). Valorando-se as variáveis do circuito \(D\) com os valores-verdade correspondentes às escolhas \(c_1,\dotsc,c_{\lvert x\rvert^k+1}\), obtemos \(\mathbf V\) como valor do circuito \(D\), pela definição do circuito \(E\).
• Se \(x\notin L\), então, toda valoração das variáveis de \(D\) induz \(\mathbf F\) como valor de \(D\), pois não há sequência de escolhas \(c\) que faça aparecer na última linha da tábua \(\mathsf T(N,x,c)\) o estado \(\qyes\). Logo, \(R\) é uma redução de \(L\) para \(\mathrm{CIRCUIT\,SAT}\).

Para concluirmos a demonstração, observe-se que como a redução simplesmente constrói \(O(1)\) portas para \(1\leq \ell\leq m\), \(0 < i\leq\lvert x\rvert^k+1\), e e \(0 < j < \lvert x\rvert^k+1\), temos que \(t_R(x)=O((\lvert x\rvert^k+1)^2)\) e, portanto, que \(R\) é polinomial. □

DEFINIÇÃO 7.23. Seja \(\Sigma\) um alfabeto ao qual não pertença o símbolo vírgula (\({,}\)), dizemos que uma Máquina de Turing Determinística \(M\) cujo alfabeto é \(\Sigma\cup\{,\}\), verifica uma linguagem \(L\subseteq\Sigma^{\ast}\) em tempo polinomial, ou que \(M\) é um verificador polinomial para \(L\), se a complexidade de tempo de \(M\) é polinomial e se existe um inteiro positivo \(k\) tal que:

1. para todo \(x\in L\), existe um certificado \(c\in\Sigma^{\ast}\) tal que \(\lvert c\rvert\leq \lvert x\rvert^k\) e \(M(x,c)=\mtyes\);
2. para todo \(x\notin L\), temos \(M(x,c)=\mtno\) para todo certificado \(c\in\Sigma^{\ast}\) com \(\lvert c\rvert\leq\lvert x\rvert^k\).

TEOREMA 7.24. Uma linguagem \(L\) está em \(\mathsf{NP}\) se e somente se existe um verificador polinomial para \(L\).

Demonstração. (Suficiência) Suponhamos que \(L\in\mathsf{NP}\), i.e. que existe uma Máquina de Turing Não-determinística \(N=(Q,\Sigma,\delta,q_0)\) que decide \(L\) em complexidade de tempo polinomial. Seja \(d_N\bydef\max_{q,s}\lvert\Delta(q,s)\rvert\). Suponhamos, sem perda de generalidade, que o símbolo \({,}\) (vírgula) não pertence ao alfabeto \(\Sigma\) de \(N\). Vamos construir uma Máquina de Turing Determinística \(M\) com complexidade de tempo polinomial que verifica \(L\). O alfabeto de \(M\) será \(\Sigma_M=\Sigma\cup\{0,\dotsc,d_N-1\}\cup\{{,}\}\), a fim de que, ao receber \((x,c)\) como entrada, \(M\) emule \(N\) para \(x\) sob a sequência de escolhas \(c\), ou devolva não se \(c\) não for uma sequência de escolhas válida. Descrevemos \(M\) com mais detalhes no pseudocódigo a seguir.

\(\underline{M(x,c)}\):

1. se \(c=i_1i_2\dotsb i_{\lvert c\rvert}\notin\{0,\dotsc,d_N-1\}^{\ast}\), devolva \(\mtno\);
2. copie \(x\) para a 2ª fita, exclusiva para a emulação de \(N\);
3. retorne o cabeçote da 2ª fita para o símbolo \(\mtstart\);
4. \(q\leftarrow q_0\);
5. para \(i\) de \(i_1\) até \(i_{\lvert c\rvert}\), faça:
6. \(\quad\) \(s\leftarrow\) símbolo lido da 2ª fita;
7. \(\quad\) se \(\lvert \Delta(q,s)\rvert\leq i\), devolva \(\mtno\);
8. \(\quad\) emule a transição \(\Delta_i(q,s)\) sobre a 2ª fita, atualizando \(q\);
9. \(\quad\) se \(q=\qyes\), devolva \(\mtyes\);
10. \(\quad\) se \(q=\qno\), devolva \(\mtno\);
11. devolva \(\mtno\).

Por construção, é imediato que a complexidade de \(M\) é polinomial em \(\lvert x,c\rvert\), uma vez que \(N\) é polinomial em \(\lvert x\rvert\), e uma vez que \(\lvert c\rvert\) é polinomial em \(\lvert x\rvert\). Argumentamos que \(M\) verifica a mesma linguagem que \(N\) decide. Como a complexidade de tempo de \(N\) é polinomial, então, existe um \(k\in\bN\) tal que \(t_N(x)\leq\lvert{x}\rvert^k\). Ainda, se \(x\in L\), então, existe uma sequência de escolhas \(c=i_1,\dotsc,i_{\lvert c\rvert}\) de comprimento \(\lvert c\rvert\leq\lvert{x}\rvert^k\) segundo a qual a computação de \(N\) para \(x\) para em \(\mtyes\). Neste caso, a máquina \(M\), quando recebe \((x,c)\), simplesmente emula a computação de \(N\) para \(x\) sob a sequência de escolhas \(c\), parando em \(\mtyes\). Por outro lado, se \(x\notin L\), para toda palavra \(c\in\Sigma_M\) temos que \(M(x,c)=\mtno\), pois:

• se \(c=i_1\dotsb i_{\lvert c\rvert}\in\{0,\dotsc,d_N-1\}^{\ast}\), mas algum \(i_j\) não representa uma escolha válida na computação de \(N\) para \(x\) segundo \(c\), ou se \(c\notin\{0,\dotsc,d_N-1\}^{\ast}\), então \(M(x,c)=\mtno\);
• se \(c=i_1\dotsb i_{\lvert c\rvert}\in\{0,\dotsc,d_N-1\}^{\ast}\) representa uma sequência de escolhas válidas para a computação de \(N\) para \(x\), temos: \(M(x,c)=\mtyes\) se a emulação da computação de \(N\) para \(x\) sob a sequência de escolhas \(c\) atinge o estado \(\qyes\); \(M(x,c)=\mtno\) em qualquer outro caso.

(Necessidade) Seja \(\Sigma\) um alfabeto tal que \({,}\notin\Sigma\), e seja \(L\subseteq\Sigma^{\ast}\) uma linguagem para a qual exista um verificador polinomial \(M\) de alfabeto \(\Sigma\cup\{{,}\}\). Vamos construir uma Máquina de Turing Não-determinística \(N\) de complexidade de tempo também polinomial para decidir \(L\). Como \(M\) verifica \(L\), seja \(k\) tal como na Definição 7.23. A Máquina \(N\), portanto, de mesmo alfabeto que \(M\), ao receber uma entrada \(x\in\Sigma^{\ast}\), tratará simplesmente de adivinhar um certificado \(c\in\Sigma^{\ast}\), de comprimento no máximo \(\lvert{x}\rvert^{k}\), e de emular \(M\) para a entrada \({(x,c)}\). Se \(x\in L\), então, existe algum certificado \(c\in\Sigma^{\ast}\) com \(\lvert c\rvert\leq\lvert x\rvert^k\) tal que \(M(x,c)=\mtyes\), o que nos traz que existe alguma computação de \(N\) para \(x\) que escolhe \(c\) apropriadamente e devolve \(\mtyes\). Por outro lado, se, para todo certificado \(c\in\Sigma^{\ast}\) com \(\lvert c\rvert\leq\lvert x\rvert^k\) vale que \(M(x,c)=\mtno\), então, todo certificado \(c\) que \(N\) adivinhar vai fazer \(N\) devolver \(\mtno\). Logo, \(N\) decide \(L\). Ademais, cada computação de \(N\) para \(x\) necessita de tempo:

• polinomial para calcular \(\lvert x\rvert ^k\) e construir, adivinhando, o certificado \(c\);
• polinomial para emular \(M\) para \((x,c)\).

Assim, \(N\) tem complexidade de tempo polinomial, como queríamos. □

Seja \(\mathrm{3SAT}\) a restrição do problema \(\mathrm{SAT}\) às instâncias em que cada cláusula possui exatamente três literais.

TEOREMA 7.25. \(\mathrm{3SAT}\) é \(\mathsf{NP}\)-completo.

Demonstração. Como \(\mathrm{3SAT}\) é uma restrição de \(\mathrm{SAT}\), temos que \(\mathrm{3SAT}\in\mathsf{NP}\). Vamos mostrar que existe uma redução polinomial \(R\) pela qual \(\mathrm{SAT}\prec_R\mathrm{3SAT}\). Nossa redução recebe uma expressão booleana \(\phi\) na CNF e devolve uma expressão booleana \(R(\phi)=\phi'\) na CNF com exatamente três literais por cláusula, de modo que \(\phi\) é satisfazível se e somente se \(\phi'\) é satisfazível. Para tanto, \(R\) quebra as cláusulas com mais de três literais de \(\phi\) em várias cláusulas, introduzindo variáveis artificiais \(z_1,z_2,\dotsc\) não presentes em \(\phi\), como esclarecido no pseudocódigo a seguir.

\(\underline{R(\phi)}\):

1. inicialize uma expressão booleana \(\phi'\) vazia na CNF;
2. \(i\leftarrow 1\);
3. para toda cláusula \(D\) de \(\phi\), faça:
4. \(\quad\) se \(D\) tem só um literal \(\ell\), então
5. \(\quad\)\(\quad\) adicione a cláusula \((\ell\vee\ell\vee\ell)\) a \(\phi'\);
6. \(\quad\) se \(D\) tem exatamente dois literais \(\ell_1\) e \(\ell_2\), então:
7. \(\quad\)\(\quad\) adicione a cláusula \((\ell_1\vee\ell_2\vee\ell_2)\) a \(\phi'\);
8. \(\quad\) se \(D\) tem exatamente três literais, então:
9. \(\quad\)\(\quad\) adicione a cláusula \(D\) a \(\phi'\);
10. \(\quad\) se \(D\) tem \(k > 3\) literais, \(\ell_1,\dotsc,\ell_k\), então:
11. \(\quad\)\(\quad\) adicione a cláusula \((\ell_1\vee\ell_2\vee z_i)\) a \(\phi'\);
12. \(\quad\)\(\quad\) para \(j\) de \(3\) até \(k-2\), faça:
13. \(\quad\)\(\quad\)\(\quad\) adicione a cláusula \((\neg z_i\vee \ell_j\vee z_{i+1})\) a \(\phi'\);
14. \(\quad\)\(\quad\)\(\quad\) \(i\leftarrow i+1\);
15. devolva \(\phi'\).

Vamos mostrar que a redução \(R\) funciona. Se uma valoração \(T\) satisfaz uma cláusula \(D\) de \(\phi\) e se o número de literais em \(D\) é no máximo três, então, há só uma cláusula em \(\phi'\) associada a \(D\), e essa cláusula, que possui o mesmo conjunto de variáveis que \(D\), também é satisfeita por \(T\). Porém, se \(D\) possui mais literais, \(\ell_1,\dotsc,\ell_k\), as \(k-2\) cláusulas \(D_2,\dotsc,D_{k-1}\) associadas a \(D\) em \(\phi'\) são, para algum inteiro positivo \(i\),

\begin{equation*} \overbrace{(\ell_1\vee \ell_2\vee z_i)}^{D_2}, \overbrace{(\neg z_i\vee \ell_3\vee z_{i+1})}^{D_3},\dotsc, \overbrace{(\neg z_{i+k-4}\vee \ell_{k-1}\vee \ell_k)}^{D_{k-1}}\,, \end{equation*}

sendo que algum literal \(\ell_j\) é satisfeito por \(T\). Note-se que a variável artificial à esquerda de \(\ell_j\) em \(D_j\), se existe, é \(z_{i+j-3}\), e a variável artificial à direita de \(\ell_j\) em \(D_j\), se existe, é \(z_{i+j-2}\). Se valorarmos, então, as variáveis \(z_i,\dotsc,z_{i+j-3}\) com \(\mathbf V\) e as variáveis \(z_{i+j-2},\dotsc,z_{i+k-4}\) com \(\mathbf F\), teremos uma valoração que satisfaz todas as cláusulas \(D_2,\dotsc,D_{k-1}\). Como as variáveis artificiais associadas a cada cláusula \(D\) de \(\phi\) são exclusivas, podemos proceder desse modo para toda cláusula de \(\phi\) e construir uma valoração para todas as variáveis de \(\phi'\) que satisfaça \(\phi'\). Assim, se \(\phi\) é satisfazível, então, \(\phi'\) também o é.

Por outro lado, suponhamos que há \(k-2\) cláusulas \(D_2,\dotsc,D_{k-1}\) em \(\phi'\) associadas a uma cláusula \(D\colon \ell_1\vee\dotsb\vee\ell_k\) em \(\phi\), e que há uma valoração \(T\) que satisfaz todas as cláusulas \(D_2,\dotsc,D_{k-1}\). Suponhamos também, a fim de contradição, que \(T\) não satisfaz literal algum de \(D\). Assim, \(T\) precisa satisfazer o literal \(z_i\) para satisfazer \(D_2\) e, consequentemente, satisfazer \(z_{i+1}\) para satisfazer \(D_3\) e, assim por diante, satisfazendo todos os literais positivos \(z_i,\dotsc,z_{i+k-4}\). Mas, assim, não há como \(T\) satisfazer \(D_{k-1}\). Logo, se \(\phi'\) é satisfazível, então \(\phi\) também o é.

A redução é de tempo polinomial porque faz uma única varredura linear sobre \(\phi\), construindo, para cada cláusula \(D\) em \(\phi\), um número linear em \(\lvert D\rvert\) de cláusulas em \(\phi'\). □

Por outro lado, \(\mathrm{2SAT}\), que é a restrição de \(\mathrm{SAT}\) às instâncias em que cada cláusula possui exatamente dois literais, pode ser resolvido em tempo polinomial.

TEOREMA 7.26. \(\mathrm{2SAT}\in\mathsf P\).

Demonstração. Vamos exibir um algoritmo determinístico polinomial que, ao receber uma instância \(\phi\) de \(\mathrm{2SAT}\), decide se \(\phi\) é satisfazível. Para tanto, note que cada cláusula \((a\vee b)\) de \(\phi\), sendo \(a\) e \(b\) literais sobre \(X(\phi)\), é logicamente equivalente às implicações \(\neg a\Rightarrow b\) e \(\neg b \Rightarrow a\), sendo a primeira a contrapositiva da segunda e vice-versa. Assim, para toda valoração \(T\) que satisfaça \(\phi\), temos com certeza que:

• \(T\) satisfaz ambos \(\neg a\) e \(b\);
• \(T\) satisfaz ambos \(\neg b\) e \(a\).

Seja, então, \(G(\phi)\) o grafo das implicações de \(\phi\), i.e. o grafo dirigido cujos vértices são todos os literais sobre \(X(\phi)=\{x_1,\dotsc,x_n\}\) e tal que para toda cláusula \((a\vee b)\) em \(\phi\), criamos ambas as arestas \(\neg a\to b\) e \(\neg b\to a\). Nesta prova, sendo \(a\) um literal, usaremos \(\neg a\) para denotar o literal \(x_i\) se \(a=\neg x_i\), ou o literal \(\neg x_i\) se \(a=x_i\).

ALEGAÇÃO. A fórmula \(\phi\) não é satisfazível se e somente se existe uma variável \(x_i\in X(\phi)\) tal que, em \(G(\phi)\), existem um caminho de \(x_i\) para \(\neg x_i\) e um caminho de \(\neg x_i\) para \(x_i\).

Demonstração da alegação. Para verificarmos a alegação, primeiro observemos que para toda instância \(\phi\) satisfazível de \(\mathrm{2SAT}\) e todo caminho de literais \(a_1a_2\dotsb a_k\) em \(G(\phi)\), é satisfazível a implicação \(a_1\Rightarrow a_k\), já que temos as clásulas \((a_1\Rightarrow a_2),(a_2\Rightarrow a_3),\dotsc,(a_{k-1}\Rightarrow a_k)\) em \(\phi\). Assim, para toda valoração \(T\) que satisfaz \(\phi\), se \(T\) satisfaz \(a_1\), então \(T\) precisa satisfazer também todos os literais \(a_2,\dotsc,a_k\).

(Necessidade) Suponhamos que para algum \(x_i\in X(\phi)\), existem um caminho de \(x_i\) a \(\neg x_i\) e um caminho de \(\neg x_i\) a \(x_i\). Suponhamos ainda, a fim de contradição, que \(\phi\) é satisfazível. Assim, são satisfazíveis ambas as implicações \(x_i\Rightarrow\neg x_i\) e \(\neg x_i\Rightarrow x_i\). Porém, para \(x_i\Rightarrow\neg x_i\) ser satisfeita por uma valoração \(T\), precisamos ter \(T(x_i)=\mathbf F\), e para \(\neg x_i\Rightarrow x_i\) ser satisfeita, precisamos ter \(T(x_i)=\mathbf V\), uma contradição.

(Suficiência) Por contraposição, suponhamos que, para todo \(x_i\in X(\phi)\), não ocorre de existirem caminhos tanto de \(x_i\) para \(\neg x_i\) quanto de \(\neg x_i\) para \(x_i\). Vamos mostrar como construir uma valoração \(T\) que satisfaça \(\phi\). Para tanto, vamos considerar cada variável \(x_i\in X(\phi)\) e definir um valor-verdade para \(T(x_i)\), marcando qual dos literais \(x_i,\neg x_i\) queremos que \(T\) satisfaça. A cada variável \(x_i\), se \(x_i\) ou \(\neg x_i\) já está marcado, pulamos para a próxima variável a ser considerada. Caso contrário, analisamos os casos que seguem.

1. Se existe caminho de \(\neg x_i\) a \(x_i\), marque \(x_i\) e todos os literais no fecho transitivo de \(x_i\). Note que, para todo literal \(a\) marcado neste passo:
   • \(a\) não é \(\neg x_i\), pois não há caminho de \(x_i\) a \(\neg x_i\);
   • \(\neg a\) não está também no fecho transitivo de \(x_i\), pois se \(x_i\Rightarrow \neg a\), temos \(x_i\Rightarrow \neg x_i\), já que, como temos \(x_i\Rightarrow a\), temos também \(\neg a\Rightarrow \neg x_i\);
   • \(\neg a\) não estava marcado, pois, como \(\neg a\Rightarrow\neg x_i\), teríamos \(\neg x_i\) marcado, mas não o temos.
2. Se existe caminho de \(x_i\) a \(\neg x_i\), marque \(\neg x_i\) e todos os literais no fecho transitivo de \(\neg x_i\). Note que, para todo literal \(a\) marcado neste passo:
   • \(a\) não é \(x_i\), pois não há caminho de \(\neg x_i\) a \(x_i\);
   • \(\neg a\) não está também no fecho transitivo de \(\neg x_i\), pois se \(\neg x_i\Rightarrow \neg a\), temos \(\neg x_i\Rightarrow x_i\), já que, como temos \(\neg x_i\Rightarrow a\), temos também \(\neg a\Rightarrow x_i\);
   • \(\neg a\) não estava marcado, pois, como \(\neg a\Rightarrow x_i\), teríamos \(x_i\) marcado, mas não o temos.
3. Se não existe caminho nem de \(x_i\) a \(\neg x_i\), nem de \(\neg x_i\) a \(x_i\), marque qualquer um dos literais \(x_i,\neg x_i\), bem como todos os literais no fecho transitivo do literal \(\ell\) arbitrado. Note que, para todo literal \(a\) marcado neste passo, \(\neg a\) não foi marcado, pois, se o tivesse sido, teríamos \(\ell\Rightarrow a\) e \(\ell\Rightarrow\neg a\), mas, como temos também \(\neg a\Rightarrow \neg\ell\), teríamos então um caminho de \(\ell\) a \(\neg\ell\) em \(G(\phi)\), uma contradição. ◊

Assim, caracterizamos a satisfazibilidade de uma instância \(\phi\) de \(\mathrm{2SAT}\) em função de uma propriedade que pode ser verificada em tempo polinomial com um algoritmo simples de busca em grafos. Portanto, \(\mathrm{2SAT}\in\mathsf P\). □

Com reduções a partir de \(\mathrm{SAT}\), podemos mostrar a \(\mathsf{NP}\)-completude de muitos outros problemas interessantes e importantes, como os que seguem.

• \(\mathrm{IS}\) (Maximum Independent Set): Dados um grafo \(G\) e um inteiro positivo \(k\), \(G\) tem um conjunto independente de tamanho \(k\)?
• \(\mathrm{CLIQUE}\): Dados um grafo \(G\) e um inteiro positivo \(k\), \(G\) tem uma clique de tamanho \(k\)?
• \(\mathrm{VC}\) (Minimum Vertex Cover): Dados um grafo \(G\) e um inteiro positivo \(k\), existe um conjunto \(X \subseteq V(G)\) com \(\lvert X\rvert = k\) tal que toda aresta de \(G\) tem pelo menos um dos extremos em \(X\)?
• \(\mathrm{DS}\) (Minimum Dominating Set): Dados um grafo \(G\) e um inteiro positivo \(k\), existe um conjunto \(X \subseteq V(G)\) com \(\lvert X\rvert = k\) tal que todo vértice de \(G\) está em \(X\) ou é vizinho de um vértice de \(X\)?
• \(\mathrm{MAX2SAT}\) (Maximum \(\mathrm{2SAT}\)): Dada uma expressão booleana \(\phi\) na CNF com exatamente dois literais por cláusula e dado um inteiro positivo \(k\), existe uma valoração das variáveis de \(\phi\) que satisfaz no mínimo \(k\) cláusulas de \(\phi\)?
• \(\mathrm{NAESAT}\) (Not-All-Equal \(\mathrm{3SAT}\)): Dada uma expressão booleana \(\phi\) na CNF com exatamente três literais por cláusula, existe uma valoração das variáveis de \(\phi\) que satisfaz no mínimo um e no máximo dois literais em cada cláusula?
• \(\mathrm{3COLOUR}\) (3-Colouring): Dado um grafo \(G\), é possível colorir os vértices de \(G\) com três cores de modo que vértices adjacentes não recebam a mesma cor?
• \(\mathrm{HP}\) (Hamiltonian Path): Dado um grafo \(G\), \(G\) tem um caminho hamiltoniano (i.e. um caminho que passa por todos os vértices de \(G\))?
• \(\mathrm{TSP}\) (Travelling Salesman Problem): Dados um grafo \(G\) completo (i.e. existe aresta entre qualquer par de vértices), uma atribuição de custos para todas as arestas de \(G\), e um inteiro \(k\), existe um ciclo hamiltoniano em \(G\) (i.e. um ciclo que passa por todos os vértices de \(G\) exatamente uma vez) cujo custo total não excede \(k\)?
• \(\mathrm{MAXCUT}\) (Maximum Cut): Dados um grafo \(G\) e um inteiro positivo \(k\), existe um conjunto \(X\subseteq V(G)\) tal que o número de arestas com um extremo em \(X\) e o outro em \(V(G)\setminus X\) é pelo menos \(k\)?
• \(\mathrm{MAXBISECT}\) (Maximum Bisection): Dados um grafo \(G\) e um inteiro positivo \(k\), existe um conjunto \(X\subseteq V(G)\) tal que \(\lvert X\rvert= \lvert V(G) \setminus X\rvert\) e tal que o número de arestas com um extremo em \(X\) e o outro em \(V(G) \setminus X\) é pelo menos \(k\)?
• \(\mathrm{BISECTWIDTH}\) (Bisection Width): Dados um grafo \(G\) e um inteiro positivo \(k\), existe um conjunto \(X\subseteq V(G)\) tal que \(\lvert X\rvert= \lvert V(G) \setminus X\rvert\) e tal que o número de arestas com um extremo em \(X\) e o outro em \(V(G) \setminus X\) é no máximo \(k\)?
• \(\mathrm{TM}\) (Perfect Tripartite Matching): Dados três conjuntos \(B\), \(G\), e \(H\) com \(n\) elementos cada e um conjunto de triplas \(E \subseteq B \times G \times H\), existe um subconjunto \(M \subseteq E\) tal que \(\lvert M\rvert= n\) e todo elemento de \(B \cup G \cup H\) aparece em \(M\) exatamente uma vez?
• \(\mathrm{SC}\) (Set Covering): Dados um conjunto \(U\), uma família \(\mathcal F\) de subconjuntos de \(U\), e um inteiro \(m\), existe uma seleção de \(m\) subconjuntos em \(F\) cuja união seja \(U\)?
• \(\mathrm{SPACKING}\) (Set Packing): Dados um conjunto \(U\), uma família \(\mathcal F\) de subconjuntos de \(U\), e um inteiro \(m\), existe uma seleção de \(m\) subconjuntos disjuntos em \(F\)?
• \(\mathrm{EC3SETS}\) (Exact Cover by 3-Sets): Dados um conjunto \(U\) com \(3m\) elementos e uma família \(\mathcal F\) de \(n\) subconjuntos de \(U\), sendo \(\lvert X\rvert= 3\) para todo \(X \in\mathcal F\), existe uma seleção de \(m\) subconjuntos disjuntos em \(\mathcal F\) cuja união seja \(U\)?
• \(\mathrm{SUBSET\,SUM}\): Dado um conjunto \(X\) de \(n\) inteiros e dado um inteiro \(t\), existe algum subconjunto \(S\) de \(X\) tal que a soma de todos os inteiros em \(S\) seja exatamente \(t\)?
• \(\mathrm{KNAPSACK}\): Dada uma coleção de \(n\) objetos, cada um com seu peso \(w_i\) e seu valor \(v_i\), e dados dois inteiros \(W\) e \(K\), existe uma seleção dos objetos cujo valor total seja pelo menos \(K\), mas cujo peso total não exceda \(W\)?
• \(\mathrm{BINPACKING}\): Dada um coleção de \(n\) objetos, cada um com seu peso \(w_i\), e dados dois inteiros \(W\) e \(B\), existe um modo de distribuir os objetos entre \(B\) caixas de modo que o peso total em cada caixa não exceda \(W\)?

TEOREMA 7.27. \(\mathrm{IS}\) é \(\mathsf{NP}\)-completo.

Demonstração. Vamos primeiro mostrar que \(\mathrm{IS}\in\mathsf{NP}\). Seja \(M\) a Máquina de Turing determinística que, ao receber um grafo \(G\), um inteiro \(k\) (supomos \(k\leq\lvert V(G)\rvert\) s.p.g.), e um conjunto \(S\) com cardinalidade no máximo a de \(G\), aceita a entrada se e somente se:

1. \(\lvert S\rvert= k\);
2. todos os elementos de \(S\) são vértices de \(G\);
3. para todo \(u\in S\) e todo \(v\in S\), \(uv\notin E(G)\).

Evidentemente, \(M\) roda em tempo \(O(\lvert S\rvert^{2} \lvert E(G)\rvert)\), i.e. polinomial no tamanho da entrada. Ainda, para toda instância \((G,k)\) do problema (novamente, supomos \(k\leq\lvert V(G)\rvert\) s.p.g.):

• se \(\langle G,k\rangle\in\mathrm{IS}\), então existe um conjunto \(S\subseteq V(G)\) que é um conjunto independente e tal que \(\lvert S\rvert=k\); assim, \(M\), ao receber \((G,k)\) acompanhado do certificado que é a descrição desse conjunto \(S\), verifica que \(\lvert S\rvert=k\), que \(S\subseteq V(G)\), e que \(S\) é um conjunto independente, aceitando a entrada;
• se \(\langle G,k\rangle\notin\mathrm{IS}\), então, para qualquer conjunto \(S\) que for passado junto com \(G\) e \(k\) como entrada para \(M\), teremos que \(\lvert S\rvert\neq k\), ou \(S\not\subseteq V(G)\), ou que \(S\) não é um conjunto independente, o que conduzirá \(M\) sempre a rejeição.

Logo, \(M\) é um verificador polinomial para \(\mathrm{IS}\).

Vamos mostrar agora que \(\mathrm{IS}\) é \(\mathsf{NP}\)-completo exibindo uma redução \(R\) de \(\mathrm{3SAT}\) a \(\mathrm{IS}\). Seja \(\phi\) uma instância de \(\mathrm{3SAT}\) com \(n\) cláusulas, recebida por \(R\), e seja \(G\) um grafo que \(R\) inicializa vazio. Para toda cláusula \(D=(a\vee b\vee c)\) de \(\phi\), a redução \(R\) cria em \(G\) um gadget triângulo com três novos vértices, um para cada literal de \(D\). Após a criação dos triângulos de todas as cláusulas, \(R\) cria uma aresta entre cada par de vértices correspondendo a literais opostos \(x\) e \(\neg x\) sobre uma mesma variável \(x\in X(\phi)\). Por fim, \(R\) atribui \(k\bydef n\) e devolve \((G,k)\). A figura a seguir ilustra o grafo \(G\) que a redução constrói para a fórmula booleana

\begin{equation*} (x_1\vee x_2\vee x_3)\wedge(\neg x_1\vee\neg x_2\vee x_3)\wedge (x_2\vee \neg x_3\vee \neg x_4) \end{equation*}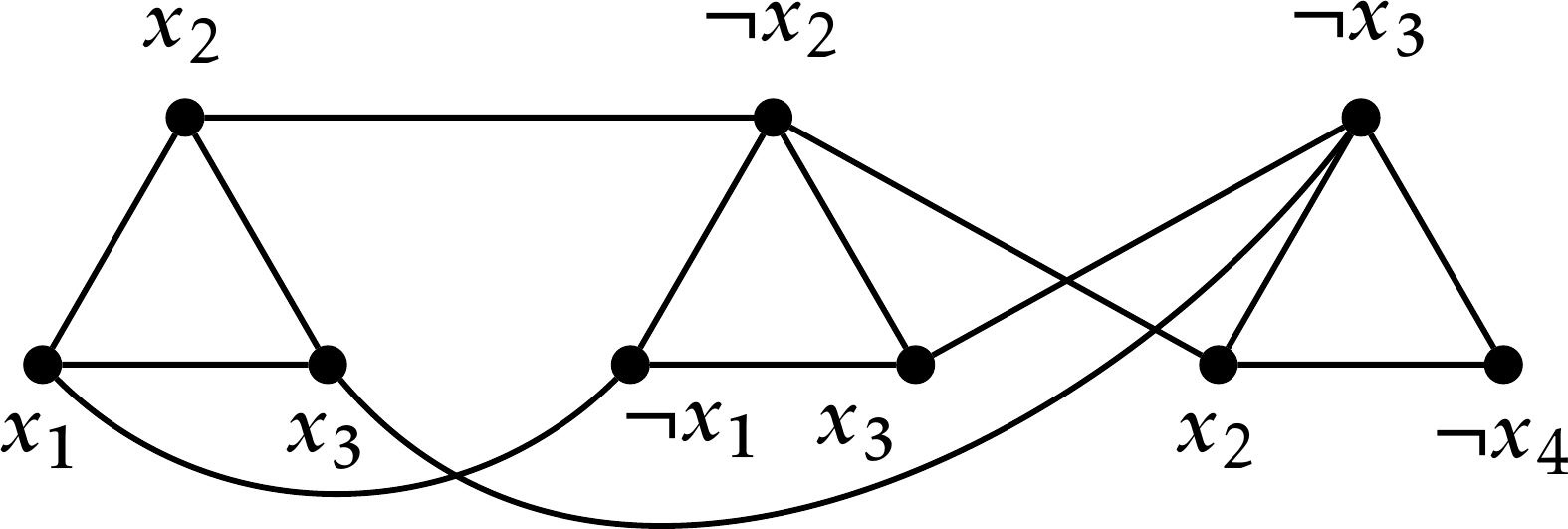

Note-se que a redução \(R\) cria um triângulo para cada cláusula de \(\phi\) e no máximo uma aresta para cada par de literais em \(\phi\); portanto, \(R\) roda em tempo \(O(n^2)\), i.e. polinomial. Ainda, para cada instância \(\phi\) de \(\mathrm{3SAT}\), vamos mostrar que \((G,k)\bydef R(\phi)\) é uma instância positiva de \(\mathrm{IS}\), i.e. que \(G\) possui um conjunto independente com \(k\) vértices, se e somente se \(\phi\) é satisfazível, concluindo a demonstração.

• Se \(\phi\in\mathrm{3SAT}\), então, seja \(T\) uma valoração que satisfaz ao menos um literal em cada cláusula e seja \(S\) um conjunto formado selecionando-se em cada gadget triângulo de \(G\) exatamente um vértice que corresponde a um dos literais que são satisfeitos por \(T\) na cláusula correspondente. Assim, \(\lvert S\rvert = k= n\). Para quaisquer dois vértices \(u,v\in S\), não temos ambos pertecendo ao mesmo gadget triângulo, e também não pode ser que \(u\) e \(v\) correspondam a literais opostos sobre uma mesma variável \(x\), já que ambos correspondem a literais que são satisfeitos por \(T\). Logo, não pode haver aresta entre \(u,v\). Portanto, \(S\) é um conjunto independente com \(k\) vértices.
• Por outro lado, se \(G\) possui um conjunto independente \(S\) com \(k=n\) vértices, então temos obrigatoriamente exatamente um vértice em \(S\) para cada um dos \(k=n\) gadgets triângulos de \(G\). Ainda, da construção de \(G\), não pode haver em \(S\) dois vértices correspondendo a literais opostos sobre uma mesma variável \(x\). Vamos construir uma valoração de \(X(\phi)\) que satisfaz \(\phi\). Para cada \(x\in $X(\phi)\): se algum vértice em \(S\) corresponde a uma ocorrência do literal \(x\), atribua \(T(x)\bydef \mathbf V\); se algum vértice em \(S\) corresponde a uma ocorrência do literal \(\neg x\), atribua \(T(x)\bydef \mathbf F\); se nenhum vértice em \(S\) corresponde a uma ocorrência de um literal sobre \(x\), arbitre \(T(x)\in\{\mathbf V,\mathbf F\}\). Note-se que \(T\) está bem definida e que para toda cláusula de \(\phi\), ao menos o literal correspondente ao vértice que está em \(S\) é satisfeito. Logo, \(T\) satisfaz \(\phi\). □

COROLÁRIO 7.28. \(\mathrm{CLIQUE}\) e \(\mathrm{VC}\) são problemas \(\mathsf{NP}\)-completos.

Demonstração. Exercício No description for this link □

TEOREMA 7.29. \(\mathrm{DS}\), \(\mathrm{MAX2SAT}\), \(\mathrm{NAESAT}\), \(\mathrm{3COLOUR}\), \(\mathrm{HP}\), \(\mathrm{TSP}\), \(\mathrm{MAXCUT}\), \(\mathrm{MAXBISECT}\), \(\mathrm{BISECTWIDTH}\), \(\mathrm{TM}\), \(\mathrm{SC}\), \(\mathrm{SPACKING}\), \(\mathrm{EC3SETS}\), \(\mathrm{SUBSET\,SUM}\), \(\mathrm{KNAPSACK}\), \(\mathrm{BINPACKING}\) são todos problemas \(\mathsf{NP}\)-completos. □

A demonstração do Teorema 7.29 é o objeto do Exercício No description for this link e do Procedimento Avaliativo em Grupos (PAG) deste curso.

1. Considere o Problema da Primalidade, definido por: Dado um número inteiro \(n\geq 2\), \(n\) é primo? Defina formalmente este problema como um problema computacional conforme a Definição 1.6. Defina também a linguagem associada a este problema de decisão.
2. Considere o Problema do Caixeiro Viajante, definido por: Dado um conjunto de cidades e dado, para cada par de cidades \((x,y)\), o custo de se viajar de \(x\) para \(y\), qual o menor custo possível de um tour que se inicie numa cidade arbitrária, passe por cada uma das cidades exatamente uma vez, e retorne à cidade de origem?. Este problema é o que chamamos de um problema de otimização (no caso, um problema de minimização).
   1. Defina formalmente o Problema do Caixeiro Viajante.
   2. Ao Problema do Caixeiro Viajante, assim como a muitos problemas de otimização, podemos associar um problema de decisão de modo que, se o problema de decisão admitir um algoritmo eficiente, então este algoritmo eficiente servirá para a composição de um algoritmo eficiente para o problema original. Defina formalmente o problema de decisão associado ao Problema do Caixeiro Viajante, argumentando por que um algoritmo eficiente para o problema de decisão implica a existência de um algoritmo eficiente para o problema de otimização original. Defina também formalmente a linguagem associada ao problema de decisão.
3. Sendo \(\Sigma\) um alfabeto qualquer, mostre que para toda linguagem \(L\) sobre \(\Sigma\) existe uma linguagem \(L_2\) sobre \(\{0,1\}\) tal que para todo \(x\in L\) corresponde um e só um \(y\in L_2\) de modo que, se \(\lvert \Sigma\rvert = 1\), então \(\lvert y\rvert=O(\log \lvert x\rvert)\), e se \(\lvert \Sigma\rvert > 1\), então \(\lvert y\rvert=O(\lvert x\rvert\lg\lvert \Sigma\rvert)\).
4. Apresente uma expressão regular e um autômato finito determinístico para a linguagem \(\{a,b\}^{\ast}\{aaba,abaa\}\) sobre o alfabeto \(\{a,b\}\).
5. Escreva uma expressão regular para a linguagem sobre o alfabeto \(\{0,1\}\) das palavras em que todo par de \(0\)s adjacentes precede todo par de \(1\)s adjacentes. Mostre também um autômato finito determinístico para esta linguagem.
6. Escreva uma expressão regular para a linguagem das palavras binárias que possuem exatamente 2 \(0\)s e pelo menos 3 \(1\)s. Mostre também um autômato finito determinístico para esta linguagem. Ainda, mostre, utilizando a expansão da função de transição estendida, que a palavra \(10101\) é aceita pelo autômato.
7. Considere a linguagem \(L\) sobre \(\Sigma\bydef\{0,1,2,\dotsc,9\}\) de todas as palavras \(w\) com comprimento pelo menos \(2\) tais que o último dígito de \(w\) aparece também em alguma outra posição de \(w\) além da última. Construa um autômato finito não-determinístico que reconhece \(L\) (tente tirar vantagem do não-determinismo para simplificar o autômato). Mostre que seu autômato aceita as palavras \(00\) e \(121\), mas rejeita as palavras \(3435\) e \(6789\).
8. Considere o problema computacional de decidir se um número inteiro não-negativo pode ser obtido através da soma de exatamente duas potências de \(4\) com expoentes inteiros, não necessariamente distintas, com expoentes inteiros.
   1. Defina este problema computacional formalmente, apresentando os conjuntos de instâncias e de soluções, e definindo a relação binária que associa a cada instância suas respectivas soluções.
   2. Defina a linguagem \(L\) sobre \(\{0,1\}\) associada a este problema de decisão, definindo a função de codificação utilizada.
   3. Apresente uma expressão regular para \(L\).
   4. Apresente um autômato finito para \(L\). Seu autômato pode ser determinístico, não-determinístico, ou não-determinístico com transições-ε.
9. Considere a linguagem \(L\) sobre \(\Sigma\bydef\{0,1\}\) definida por \(L\bydef\{0^n10^n\mathbin : n\in\bN\}\). Prove ou refute: \(L\) é uma linguagem regular.
10. Considere a linguagem unária das palavras que codificam os quadrados perfeitos, isto é, a linguagem \(L\) sobre \(\Sigma\bydef\{1\}\) definida por \[L\bydef\{1^n\mathbin : \text{$n\in\bZ_{> 0}$ é um quadrado perfeito}\}\,.\] Mostre que esta linguagem não é regular.
11. Prove ou refute:
    1. Todo subconjunto de uma linguagem regular é uma linguagem regular.
    2. Toda linguagem finita é regular.
    3. A união de duas linguagens regulares é uma linguagem regular.
    4. A concatenação de duas linguagens regulares é uma linguagem regular.
    5. Se \(L\) é uma linguagem regular, então \(L^{\ast}\) também é uma linguagem regular.
    6. O complemento de uma linguagem regular é uma linguagem regular.
    7. A interseção de duas linguagens regulares é uma linguagem regular.
    8. Sendo \(L_1\) e \(L_2\) duas linguagens regulares, \(L_1\setminus L_2\) também é regular.
    9. A linguagem binária \(L=\{0^i1^j\mathbin : i\neq j\}\) é regular.
12. Mostre que a linguagem definida no Exercício 1 não é regular.

13. Considere as seguintes linguagens sobre o alfabeto \(\{0,1\}\).

    \begin{align*} A &= \{w\in\{0,1\}^{\ast}\mathbin : \#0(w) = \#1(w)\}\\ B &= \{w\in\{0,1\}^{\ast}\mathbin : \#0(w) = 3\}\\ C &= \{w\in\{0,1\}^{\ast}\mathbin : \lvert \#0(w) - \#1(w)\rvert\geq3\}\\ L_1 &= AB\\ L_2 &= A\setminus (C\{0,1\}^{\ast}) \end{align*}

    Seja \(i\in\{1,2\}\) tal que \(L_i\) é regular, e seja \(j=(i\bmod 2)+1\).

    1. Mostre que \(L_i\) é regular, exibindo um autômato finito determinístico para \(L_i\).
    2. Mostre que \(L_j\) não é regular.
14. Mostre que, para toda linguagem unária \(L\) (i.e. \(L\subseteq\Sigma^{\ast}\) e \(\lvert\Sigma\rvert=1\)), \(L^{\ast}\) é sempre regular, mesmo quando \(L\) não é regular. Exiba também um contraexemplo para essa afirmação quando aplicada sobre linguagens binárias, i.e. exiba uma linguagem binária \(L\) e prove que ambas \(L\) e \(L^{\ast}\) não são regulares.
15. O Lema de Bombeamento estabelece uma condição necessária para linguagens regulares, porém não suficiente. Mostre que a seguinte linguagem satisfaz a condição do lema, mas não é regular (dica: para mostrar que não é regular, utilize o Exercício 11): a linguagem sobre \(\Sigma=\{a,b,c\}\) dada por \(L=\{ab^nc^n\mathbin : n\geq 0\}\cup\{a^kw\mathbin : k\neq 1\text{ e }w\notin \{a\}\Sigma^{\ast}\}\).
16. Seja \(x\) uma palavra sobre um alfabeto \(\Sigma\) e seja \(L\) a linguagem das palavras que não contêm \(x\) como subpalavra. Prove ou refute: \(L\) é uma linguagem regular.
17. Considere a linguagem \(L\) sobre \(\{(,)\}\) das palavras de parênteses bem formados. Por exemplos, \(\upeps\), \(()\), \((())\), e \(()()\) são todos exemplos de palavras em \(L\), mas \(())(()\) não é. Construa uma gramática \(\Gamma\) e mostre que \(L(\Gamma)=L\).
18. Considere a linguagem \(L\) sobre \(\{a,b,{+},{-},{*},{/},{(},{)}\}\) das expressões aritméticas bem formadas envolvendo os símbolos \(a\) e \(b\), as operações do conjunto \(\{{+},{-},{*},{/}\}\), e parênteses. Por exemplos, \(a+b\), \(\upeps\), e \(ab/(a+b)\) são palavras em \(L\).
    1. Construa uma gramática livre de contexto para \(L\).
    2. Construa um autômato com pilha que aceita \(L\) por estado final.
    3. Construa um autômato com pilha que aceita \(L\) por pilha vazia.

19. Mostre que, sendo \(A\) o AP definido pelo diagrama de transições a seguir, \(L(A)\) é a linguagem dos palíndromos binários de comprimento par.

    

20. Construa uma gramática livre de contexto \(\Gamma\) para a linguagem \(L_j\) do Exercício 13. Prove que, de fato, \(L(\Gamma)=L_j\).
21. Construa uma gramática livre de contexto para a linguagem sobre \(\{a,b,c\}\) definida por \(L\bydef\{a^ib^jc^k\mathbin : i\neq j\text{ ou }j\neq k\}\). Construa também um autômato com pilha que aceita \(L\) (por pilha vazia ou por estado final, você que escolhe).
22. Sendo \(\Gamma=(V, \Sigma, {\to}, S)\) uma GLC, sendo \(X\to \gamma\) uma produção de \(\Gamma\), e sendo \(\alpha,\beta\in(V\cup\Sigma)^{\ast}\), dizemos que a derivação \(\alpha X\beta\Rightarrow \alpha\gamma\beta\) é uma derivação mais à esquerda (mais à direita), e escrevemos \(\alpha X\beta\Rightarrow\def\desq{_{\mathrm{esq}}}\desq \alpha\gamma\beta\) (\(\alpha X\beta\Rightarrow\def\ddir{_{\mathrm{dir}}}\ddir \alpha\gamma\beta\)) se \(\alpha\in\Sigma^{\ast}\) (\(\beta\in\Sigma^{\ast}\)). Usando o conceito de árvore de derivação, mostre, para todo \(\alpha\in(V\cup\Sigma)^{\ast}\), que \(\Gamma\overset{\ast}\Rightarrow\desq \alpha\) (\(\Gamma\overset{\ast}\Rightarrow\ddir \alpha\)) se e somente se \(\Gamma\overset{\ast}\Rightarrow \alpha\).
23. Construa uma gramática livre de contexto para a linguagem \(L\) das palavras binárias cujo número de \(0\)s é o dobro do número de \(1\)s. Construa também um autômato com pilha que aceita \(L\) por estado final. Mostre que seu autômato aceita \(001010\) e rejeita \(01010\).
24. Usamos \(\overleftarrow x\) para denotar o reverso da palavra \(x\), i.e. se \(x=s_1s_2\dotsb s_{n-1}s_n\) então \(\overleftarrow x=s_ns_{n-1}\dotsb s_2s_1\). A linguagem \(L=\{x\overleftarrow x x\mathbin : x\in\{0,1\}^{\ast}\}\) é regular? E livre de contexto? Prove ambas as suas respostas.
25. Num tabuleiro de xadrez infinito sobre o plano cartesiano, um rei está numa dada casa \((i,j)\), com \(i,j\in\mathbb Z\). Nesta variante do xadrez, contudo, o rei não pode se mover nas diagonais. Apenas quatro movimentos são possíveis: \(R\), em que o rei vai da casa \((i,j)\) para a casa \((i,j+1)\); \(U\), em que o rei vai da casa \((i,j)\) para a casa \((i+1,j)\); \(L\), em que o rei vai da casa \((i,j)\) para a casa \((i,j-1)\); \(D\), em que o rei vai da casa \((i,j)\) para a casa \((i-1,j)\). Seja \(L\) a linguagem de todas as palavras formadas por uma sequência de movimentos que fazem o rei retornar à casa de onde começou a sequência. São exemplos de palavras de \(L\): \(RL\), \(RULD\), \(RLRL\), \(RULLDDRU\) etc. Esta linguagem é regular? E livre de contexto? Prove ambas as suas respostas.
26. Construa uma MTD de uma só fita que, dado um inteiro não-negativo \(n\) codificado em binário (big endian), computa o dobro de \(n\). Exiba a computação, a saída e o tempo de sua máquina para as instâncias \(1\), \(7\), e \(0\), apresentando também, e justificando, a complexidade de tempo.
27. Construa uma MTD com múltiplas fitas, complexidade de tempo linear e um só estado não-final que, dados dois inteiros não-negativos \(n_1\) e \(n_2\), codificados em binário e separados por uma vírgula, computa a soma dos dois números. Exiba a computação, a saída e o tempo de sua Máquina para as instâncias \((0,0)\), \((5,2)\) e \((7,1)\), apresentando também, e justificando, a complexidade de tempo.
28. Construa uma MTD com múltiplas fitas que, dadas duas palavras binárias não-vazias \(x_1\) e \(x_2\) separadas por uma vírgula, decide se \(x_1\) é subpalavra de \(x_2\). Exiba a computação, a saída e o tempo de sua Máquina para as instâncias \(1{,}1\), \(101{,}10011010\) e \(0{,}111\), apresentando também, e justificando, a complexidade de tempo.
29. Construa uma Máquina de Turing não-determinística de uma só fita que, dada uma palavra \(x=b_{1a}b_{1b}b_{2a}b_{2b}\dotsb b_{na}b_{nb}\) de comprimento \(2n\), sendo \(n\) um inteiro positivo, decide se existe uma subpalavra \(y=b_1b_2\dotsb b_n\) de \(x\) tal que \(b_j\in\{b_{ja},b_{jb}\}\) para todo \(j\in\{1,\dotsc,n\}\) e tal que o número de bits iguais a \(0\) em \(y\) é igual ao número de bits iguais a \(1\) em \(y\).
30. Considere o seguinte problema computacional de decisão: Dadas uma Máquina de Turing \(M\) e uma entrada \(x\) para \(M\), a computação de \(M\) para \(x\) usa todos os estados não-finais de \(M\)? Este problema é decidível? Justifique sua resposta.
31. Considere o seguinte problema computacional de decisão: Dada uma Máquina de Turing \(M\), a linguagem \(L(M)\) é finita? Este problema é decidível? Justifique sua resposta.
32. Considere o seguinte problema computacional de decisão: Dadas duas Máquinas de Turing \(M_1\) e \(M_2\), \(L(M_1)=L(M_2)\)? Este problema é decidível? Justifique sua resposta.
33. Mostre que toda linguagem decidível pode ser reduzida para a linguagem do Problema da Parada.
34. Sendo \(U\) a Máquina de Turing Universal, mostre que \(L(U)\) é recursivamente enumerável, mas não recursiva.
35. Seja \(L\bydef\{\langle M\rangle\mathbin : M\text{ é uma Máquina de Turing tal que todas as palavras de }E(M)\text{ terminam em }0\}\). Escolha um entre os conjuntos \(\mathsf R\), \(\mathsf{RE}\setminus\mathsf{R}\), \(\mathsf{coRE}\setminus\mathsf{R}\), \(\Sigma_U^{\ast}\setminus(\mathsf{RE}\cup\mathsf{coRE})\). Mostre que \(L\) pertence ao conjunto que você escolheu.
36. Considere as linguagens \(L_1=\{\langle M\rangle\mathbin : M(\langle M\rangle)=\mtyes\}\) e \(L_2=\{\langle M\rangle\mathbin : M(\langle M\rangle)=\mtno\}\). Para cada \(i\in\{1,2\}\), escolha um entre os conjuntos \(\mathsf R\), \(\mathsf{RE}\setminus\mathsf{R}\), \(\mathsf{coRE}\setminus\mathsf{R}\), \(\Sigma_U^{\ast}\setminus(\mathsf{RE}\cup\mathsf{coRE})\), e mostre que \(L_i\) pertence ao conjunto que você escolheu.
37. Mostre que os seguintes problemas são indecidíveis:
    1. Dada uma Máquina de Turing Não-determinística \(N\) com alfabeto \(\Sigma\), é verdade que, para todo \(x\in\Sigma^{\ast}\), todas as computações de \(M\) para \(x\) param?
    2. Dada uma Máquina de Turing Não-determinística \(N\) com alfabeto \(\Sigma\), é verdade que, para toda entrada \(x\), ou todas as computações de \(N\) para \(x\) terminam em rejeição, ou pelo menos metade das computações possíveis de \(N\) para \(x\) terminam em aceitação e as demais terminam em rejeição?
    3. Dada uma Máquina de Turing Não-determinística \(N\) com alfabeto \(\Sigma\), é verdade que, para toda entrada \(x\), ou pelo menos \(2/3\) das computações de \(N\) para \(x\) terminam em aceitação e as demais em rejeição, ou pelo menos \(2/3\) das computações de \(N\) para \(x\) terminam em rejeição e as demais em aceitação?
38. Duas linguagens \(L_1\) e \(L_2\) são ditas: recursivamente separáveis se existe uma linguagem recursiva \(X\) tal que \(L_1\cap X=\emptyset\) e \(L_2\subseteq X\); recursivamente inseparáveis se não existe tal linguagem recursiva \(X\). Mostre que as linguagens \(L_1\) e \(L_2\) do Exercício 36 são recursivamente inseparáveis.