Matemática Discreta (ICSD21)
Sumário
- Bibliografia
- AULA 1: Introdução a Matemática Discreta e demonstrações
- AULA 2: Demonstrações por indução
- AULA 3: Mais exemplos de demonstrações sobre divisibilidade
- AULA 4: Relações, funções, e operações
- AULA 5: Introdução a sequências, recorrências, e algoritmos recursivos
- AULA 6: Recorrências lineares
- AULA 7: Análise Combinatória
- AULA 8: Introdução a Teoria dos Grafos
- AULA 9: Enumerabilidade
- Lista de exercícios
- ATENÇÃO! As Notas de Aula presentes nesta página são meras (e incompletas) anotações, propositalmente sucintas, servindo apenas para guiar o estudante em seus estudos e padronizar convenções, não tomando de modo algum o lugar da bibliografia do curso, e não representando de modo algum a totalidade do conteúdo ou a metodologia didática daquilo que é trabalhado em sala de aula. Apesar do nome, algumas Aulas neste material podem corresponder a várias aulas reais, conforme o planejamento de ensino.
- Caso encontre algum erro nestas anotações ou queira fazer uma sugestão, por favor não hesite em entrar em contato.
- Os exemplos e exercícios listados aqui foram selecionados visando maximizar o aproveitamento do conteúdo dadas as restrições limitadas de ementa e carga horária do curso de Matemática Discreta da UTFPR-CT. Para muito mais exemplos e exercícios, consulte também a bibliografia do curso.
- Deixo registrado meu agradecimento à Profª Drª Marina E. Groshaus pelas grandes contribuições que fez a este material.
Bibliografia
AULA 1: Introdução a Matemática Discreta e demonstrações
- Base: [Ros12] Prefácio e Sec. 1.7–1.8; [Ger14] Sec. 2.1; [Vel06] Cap. 3; [CLRS09] Sec. 31.1
- Exercícios: 1–7
Uma demonstração direta de uma implicação \(A\Rightarrow B\) consiste em, supondo \(A\), derivar \(B\). Para o exemplo do Teorema 1.1, dizemos que um inteiro \(a\) é divisor de um inteiro \(b\) se existe um inteiro \(k\) tal que \(b=ak\).
TEOREMA 1.1. Todo número inteiro é divisor de zero.
Demonstração. Seja \(a\) um número inteiro qualquer. Queremos mostrar que existe um inteiro \(k\) tal que
\begin{equation} \label{eqteo1p1} 0=a\cdot k\,. \end{equation}Ora, para tanto, basta tomarmos \(k=0\), que é um inteiro, e assim obtemos \eqref{eqteo1p1}, como queríamos. □
TEOREMA 1.2. O quadrado de todo número inteiro ímpar também é um número inteiro ímpar.
Demonstração. Seja \(a\) um número inteiro ímpar. Então, por definição, \(a\) pode ser escrito na forma \(a=2k+1\) para algum inteiro \(k\). Consequentemente,
\begin{align*} a^2 &= (2k+1)^2 = 4k^2+4k+1\\ &= 2(2k^2+2k) + 1\,, \end{align*}o que implica que \(a^2\) pode ser escrito na forma \(a^2=2q+1\), com \(q=2k^2+2k\) inteiro. Logo, \(a^2\) também é um número inteiro ímpar. □
Da Lógica Proposicional, sabemos que as implicações \(A\Rightarrow B\) e \(\neg B\Rightarrow \neg A\) são equivalentes (uma é a contrapositiva da outra). Assim, uma demonstração por contraposição de uma implicação \(A\Rightarrow B\) consiste em, supondo \(\neg B\), derivar \(\neg A\).
TEOREMA 1.3. Se um número inteiro não é par, então também não é múltiplo de \(\,4\).
Demonstração. Por contraposição, vamos mostrar que todo número inteiro que é múltiplo de \(4\) é também par. Seja \(a\) um inteiro múltiplo de \(4\). Então, temos um inteiro \(k\) tal que \(a=4k\), e, portanto, \(a=2(2k)\). Logo, para o inteiro \(q=2k\), temos que \(a\) pode ser escrito como \(a=2q\). Logo, \(a\) é par. □
TEOREMA 1.4. Para todo inteiro \(a\), se \(a^2\) é par, então \(a\) também é par.
Demonstração. Seja \(a\) um inteiro. Como a contrapositiva de
"se \(a^2\) é par, então \(a\) também é par"
é
"se \(a\) é ímpar, então \(a^2\) também é ímpar",
a prova segue do Teorema 1.2. □
Nem sempre queremos provar afirmações. Às vezes, queremos refutá-las. Uma técnica muito útil para refutar afirmações é através da exibição de contraexemplos.
EXERCÍCIO RESOLVIDO 1.5. Prove ou refute: todo inteiro divisível por \(\,6\) e maior que \(\,6\) é também divisível por \(\,4\).
Resolução. Basta tomar \(18\), que é divisível por \(6\), mas não o é por \(4\). □
TEOREMA 1.6. Todo divisor comum entre dois inteiros \(a\) e \(b\) é também um divisor de \(b - a\).
Demonstração. Seja \(d\) um divisor comum entre \(a\) e \(b\), i.e. \(d\) é um inteiro para o qual existem \(k_1,k_2\in\def\bZ{\mathbb Z}\bZ\) tais que
\begin{align*} a &= dk_1\quad\text e\\ b &= dk_2\,. \end{align*}Assim,
\begin{equation*} b - a = d(k_2 - k_1)\,. \end{equation*}Como \(k_2-k_1\) é um inteiro, temos, portanto, que \(d\) é um divisor de \(b-a\). □
Devemos sempre tomar cuidado ao interpretar demonstrações. Por exemplo, a demonstração do Teorema 1.6 não necessariamente implica que \(d=(b-a)/(k_2-k_1)\), já que, se \(a=b\), temos \(k_1=k_2\) e, portanto, \(k_2-k_1=0\). Mas isso não invalida o enunciado do teorema, nem a demonstração. De fato, quando \(a=b\), todo divisor de \(a=b\) é um divisor de \(0\), como já sabíamos do Teorema 1.1.
Para a demonstração a seguir, um exemplo de uma demonstração por contraposição, recorde-se da Lógica Proposicional que a disjunção \(A\vee B\) é equivalente à implicação \(\neg A\Rightarrow B\) por definição desta.
TEOREMA 1.7. Sejam \(x\) e \(y\) números reais. Se \(x^2+y=13\) e \(y\neq 4\), então \(x\neq 3\).
Demonstração. Sendo \(x\) e \(y\) números reais, suponhamos que \(x=3\). Vamos mostrar que \(x^2+y\neq 13\) ou \(y=4\). Para tanto, vamos mostrar que se \(x^2+y= 13\), então \(y=4\).
Suponhamos então que \(x^2+y=13\). Queremos mostrar que \(y=4\). Ora, como \(x=3\), temos que
\begin{equation*} 3^2+y=13\,, \end{equation*}o que nos traz que \(y=4\) como queríamos. □
Recorde-se também da Lógica Proposicional que, por definição, uma implicação \(A\Rightarrow B\) é verdadeira também quando o antecedente (a premissa, ou hipótese) \(A\) é falso. Uma demonstração por vacuidade é uma demonstração em que, para provar \(A\Rightarrow B\), provamos que \(A\) é sempre falso. Para a demonstração a seguir, recorde-se ainda que dizemos que um conjunto \(X\) é subconjunto de um conjunto \(Y\), e escrevemos \(X\subseteq Y\), se, para todo \(x\), vale a implicação \(x\in X\Rightarrow x\in Y\).
TEOREMA 1.8. O conjunto vazio é subconjunto de todo conjunto.
Demonstração. Seja \(X\) um conjunto qualquer. Queremos provar que \(\emptyset\subseteq X\), i.e. queremos provar, para todo \(x\), que é verdadeira a implicação
\begin{equation} \label{eqvazio} x\in\emptyset\Rightarrow x\in X\,. \end{equation}Como \(x\notin\emptyset\), por definição de conjunto vazio, temos que o antecedente de \eqref{eqvazio} é sempre falso e, portanto, que a implicação é verdadeira por vacuidade. □
Quando vamos mostrar uma equivalência \(A\Leftrightarrow B\), precisamos mostrar que \(A\) é condição tanto suficiente para \(B\) (isto é, \(A\Rightarrow B\)) quanto necessária (isto é, \(A\Leftarrow B\)).
TEOREMA 1.9. Um número inteiro \(n\) é múltiplo de \(\,6\) se e somente se é múltiplo de \(\,2\) e múltiplo de \(\,3\).
Demonstração. Seja \(n\) um inteiro.
(Suficiência) Suponhamos que \(n\) seja múltiplo de \(6\), i.e. que \(n=6k\) para algum inteiro \(k\). Vamos mostrar que \(n\) também é múltiplo de \(2\) e de \(3\), i.e. que existem \(k_1\) e \(k_2\) inteiros tais que \(n=2k_1\) e \(n=3k_2\). Ora, como \(n=6k=2(3k)=3(2k)\), basta tomarmos \(k_1=3k\) e \(k_2=2k\).
(Necessidade) Suponhamos que \(n\) seja múltiplo de \(2\) e de \(3\), i.e. que existam \(k_1\) e \(k_2\) inteiros tais que \(n=2k_1=3k_2\). Queremos mostrar que \(n\) também é um múltiplo de \(6\), i.e. que existe um inteiro \(k\) tal que \(n=6k\). Ora,
\begin{align*} n&=3n - 2n\\ &= 3(2k_1) - 2(3k_2)\\ &= 6(k_1 - k_2)\,. \end{align*}Assim, para \(k=k_1-k_2\), temos \(n=6k\), como queríamos. □
Uma demonstração por contradição, ou por reductio ad absurdum (redução ao absurdo), de uma implicação \(A\Rightarrow B\) consiste em, supondo \(A\) e também \(\neg B\), derivar uma contradição.
TEOREMA 1.10. Sejam \(x\) e \(y\) números reais não ambos iguais a zero. Se \(x+y=2y-x\), então \(y\neq 0\).
Demonstração. Suponhamos que \(x+y=2y-x\) e, a fim de contradição, que \(y=0\). Então, temos
\begin{align*} &&x+0&=2\cdot 0-x\,,\\ \text{portanto}&& x&=-x\,,\\ \text{portanto}&& x+x&=x-x\,,\\ \text{portanto}&& 2x &=0\,,\\ \text{e, assim,}&& x &= \frac02 = 0\,, \end{align*}contradizendo o fato de que \(x\) e \(y\) não são ambos iguais a zero. □
Demonstrações por contradição também podem ser úteis para refutar afirmações.
EXERCÍCIO RESOLVIDO 1.11. Prove ou refute: é possível construir um conjunto de \(\,22\) dias em que não há \(\,4\) elementos que possam ser selecionados de modo a caírem todos no mesmo dia da semana.
Resolução. Vamos refutar a afirmação, i.e. vamos provar que, em qualquer conjunto de \(22\) dias, sempre é possível selecionar \(4\) elementos de modo a caírem todos no mesmo dia da semana. A fim de contradição, suponhamos que exista um conjunto \(X\) com \(22\) dias em que não há \(4\) elementos que possam ser selecionados de modo a caírem todos no mesmo dia da semana, i.e. que, para toda seleção \(S\subseteq X\) de dias que caem no mesmo dia da semana, temos \(\lvert S\rvert \leq 3\). Para cada \(i\)-ésimo dia da semana, seja \(S_i\) o conjunto dos elementos de \(X\) que caem naquele dia. Como o número de elementos em \(X\) é a soma dos números de elementos em \(S_1,S_2,\dotsc,S_7\), e como, por hipótese, \(\lvert S_i\rvert \leq 3\) para todo \(i\), temos que \(X\) pode ter no máximo \(21\) elementos, uma contradição. □
TEOREMA 1.12. A raiz quadrada de \(\,2\) é um número irracional.
Demonstração. Suponhamos que \(\sqrt 2\) seja um número racional, isto é, que existam dois inteiros \(a\) e \(b\) tais que \(\sqrt 2=a/b\). Sem perda de generalidade, podemos supor que \(a\) e \(b\) são coprimos, pois, caso \(\gcd(a,b)>1\), poderíamos substituir \(a\) e \(b\) pelos inteiros \(a'=a/\gcd(a,b)\) e \(b'=b/\gcd(a,b)\), respectivamente, os quais são coprimos e satisfazem
\begin{equation*} \frac{a'}{b'} = \frac ab = \sqrt 2\,. \end{equation*}Como \(\sqrt 2=a/b\) implica \(a^2=2b^2\), temos que \(a^2\) é um número par, o que nos traz, pelo Teorema 1.2 que \(a\) também é um número par, isto é, que \(a=2k\) para algum inteiro \(k\). Então,
\begin{equation*} (2k)^2=2b^2 \end{equation*}e, portanto,
\begin{equation*} b^2=2k^2\,, \end{equation*}o que nos traz que \(b^2\) é um número par e, do Teorema 1.2 que \(b\) também é um número par, um absurdo, já que \(a\) e \(b\) são coprimos. □
A demonstração a seguir é um exemplo de uma demonstração de existência não-construtiva.
TEOREMA 1.13. Existem dois números irracionais \(x\) e \(y\) tais que \(x^y\) é um número racional.
Demonstração. Se \((\sqrt 2)^{\sqrt 2}\) é racional, então podemos tomar \(x=y=\sqrt 2\), já que \(\sqrt 2\) é irracional (cf. Teorema 1.12). Por outro lado, se \((\sqrt 2)^{\sqrt 2}\) é irracional, então, como
\begin{equation*} \Bigl( (\sqrt 2)^{\sqrt 2} \Bigr)^{\sqrt 2}= (\sqrt 2)^{(\sqrt 2)(\sqrt 2)}=(\sqrt 2)^{ 2} = 2\,, \end{equation*}podemos tomar \(x=(\sqrt 2)^{\sqrt 2}\) e \(y=\sqrt 2\). □
Pré-lista de exercícios
- Mostre que o produto de dois quadrados perfeitos é também um quadrado perfeito.
- Não se deve confundir a contrapositiva \(\neg B\Rightarrow\neg A\) de uma
implicação \(A\Rightarrow B\) com sua recíproca \(B\Rightarrow A\).
Indique o antecedente e o consequente de cada uma das sentenças
abaixo. Escreva também a contrapositiva e a recíproca de cada uma
delas.
- O crescimento sadio das plantas é conseqüência de quantidade suficiente de água.
- O crescimento da oferta de computadores é uma condição necessária para o desenvolvimento científico.
- Haverá novos erros apenas se o programa for alterado.
- A economia de combustível implica um bom isolamento, ou todas as janelas são janelas para tempestades.
- Mostre que a raiz quadrada de todo primo par maior que \(2\) é \(\int_1^{\pi}\frac{dx}x\).
A Conjectura de Goldbach é a asserção de que todo número par maior que \(2\) pode ser escrito como a soma de dois números primos. A Conjectura Fraca de Goldbach, para a qual uma prova foi anunciada em 2013, é a asserção de que todo número ímpar maior que \(5\) pode ser escrito como a soma de três primos. Por exemplos:
\begin{align*} 4&=2+2 & 6 &=3+3 & 8 &= 3 + 5\\ 10 &= 3 + 7 = 5 + 5 & 7 &= 2+2+3 & 9&= 3 + 3 + 3 \\ 11 &= 3 + 3 + 5 & 13 &= 3 + 3 + 7 = 3 + 5 + 5 \end{align*}Observe que, para estes números, estas são todas as somas de dois (caso par) ou três (caso ímpar) primos. Mostre que a Conjectura de Goldbach implica a Conjectura Fraca de Goldbach.
Considere a seguinte tentativa de demonstração, errada, de que \(\sqrt 4\) é um número irracional.
Suponhamos que \(\sqrt 4\) seja um número racional, isto é, que existam dois inteiros \(a\) e \(b\) tais que \(\sqrt 4=a/b\). Sem perda de generalidade, podemos supor que \(a\) e \(b\) são coprimos, pois, caso \(\gcd(a,b)>1\), poderíamos substituir \(a\) e \(b\) pelos inteiros \(a'=a/\gcd(a,b)\) e \(b'=b/\gcd(a,b)\), respectivamente, os quais são coprimos e satisfazem \(a'/b'= a/b =\sqrt 4\). Como \(\sqrt 4=a/b\) implica \(a^2=4b^2\), temos que \(a\) é um número divisível por \(4\), isto é, que \(a=4k\) para algum inteiro \(k\). Então, \((4k)^2=4b^2\) e, portanto, \(b^2=4k^2\), o que nos traz que \(b^2\) é um número divisível por \(4\) e, consequentemente, que \(b\) também é um número divisível por \(4\), um absurdo, já que \(a\) e \(b\) são coprimos. □
Qual o problema com ela?
AULA 2: Demonstrações por indução
Sendo \(\def\bR{\mathbb R}x\in\bR\setminus\{0\}\) e \(n\in{\mathbb Z}_{\geq 0}\), a \(n\)-ésima potência de \(x\) é definida como:
\begin{equation*} x^n = \left\{ \begin{aligned} & 1,&&\text{se \(n = 0\);}\\ & x\cdot x^{n-1},&&\text{se \(n > 0\).} \end{aligned} \right. \end{equation*}Definições recursivas são bastante usadas em Matemática Discreta, e costumam ser vantajosas para a construção de provas por indução sobre os conceitos definidos, como na demonstração do Teorema 2.1.
TEOREMA 2.1. Sendo \(n\) um inteiro positivo qualquer, \(2^n > n\).
Demonstração. Seja \(n\) um inteiro não-negativo qualquer. Se \(n=1\), temos
\begin{equation*} 2^n=2 > n =1\,, \end{equation*}como queríamos. Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que, para todo inteiro \(k\) satisfazendo \(1 \leq k < n\), valha que \(2^k > k\). Como \(n > 1\), temos, da definição formal de potência, que
\begin{equation} \label{eqind1} 2^n = 2\cdot 2^{n-1} \end{equation}e, da hipótese da indução, já que \(1\leq n - 1 < n\), que
\begin{equation} \label{eqind2} 2^{n-1} > n - 1\,. \end{equation}De \eqref{eqind1} e \eqref{eqind2}, obtemos
\begin{equation*} 2^n > 2(n-1) = (n-1)+(n-1) \end{equation*}e, como \(n-1\geq 1\),
\begin{equation*} 2^n > (n-1)+(n-1)\geq (n-1)+1=n\,, \end{equation*}como queríamos. □
Apresentamos a seguir duas demonstrações válidas para um mesmo teorema: uma direta e outra por indução.
TEOREMA 2.2. Sendo \(n\) um inteiro não-negativo qualquer, \(1+2+\dotsb+n = n(n+1)/2\).
Demonstração (direta). Seja \(n\) um inteiro não-negativo. Queremos mostrar que \(S\def\bydef{\mathbin{:=}}\def\fedyb{\mathbin{=:}}\bydef\sum_{i=1}^n i = n(n+1)/2\). Da comutatividade da soma, temos que
\begin{align*} \sum_{i=1}^n i&=1+2+\dotsb+(n-1)+n\\ & = n + (n-1) +\dotsb +2 + 1\\ &= \sum_{i=1}^n (n-i+1)\,, \end{align*}e, portanto,
\begin{align*} 2S &= \sum_{i=1}^n i+ \sum_{i=1}^n (n-i+1)\\ &=\sum_{i=1}^n (i + n - i + 1)\\ &= \sum_{i=1}^n (n + 1)\\ &= n(n+1)\,. \end{align*}Logo, \(S=n(n+1)/2\), como queríamos mostrar. □
Demonstração (por indução). Seja \(n\) um inteiro não-negativo. Queremos mostrar que \(\sum_{i=1}^n i = n(n+1)/2\). Se \(n=0\), temos que \(\sum_{i=1}^0 i = 0 = 0(0+1)/2\), como desejado. Suponhamos, então, que \(n>0\) e, por indução em \(n\), que para todo inteiro não-negativo \(k < n\) valha que \(\sum_{i=1}^{k} i = k(k+1)/2\). Ora, sabemos que
\begin{equation*} \sum_{i=1}^{n} i=n + \sum_{i=1}^{n-1} i \end{equation*}e, da hipótese da indução, que
\begin{equation*} \sum_{i=1}^{n-1} i=\frac{(n-1)n}2\,. \end{equation*}Portanto,
\begin{align*} \sum_{i=1}^{n} i&=n + \frac{(n-1)n}2\\ &= n\Bigl(1+\frac{n-1}2\Bigr)=\frac{n(n+1)}2\,, \end{align*}como queríamos. □
TEOREMA 2.3. Para todo inteiro \(n \geq 4\), vale que \(n^2 > 6n-9\).
Demonstração. Se \(n=4\), temos \(n^2=16 > 15 =6n-9\), como queríamos. Suponhamos, então, que \(n \geq 5\) e, por indução, que para todo inteiro \(k\) satisfazendo \(4\leq k < n\) valha que \(k^2 > 6k-9\). Ora,
\begin{equation*} n^2 = (n-1)^2 + 2(n-1) + 1\,, \end{equation*}e, da hipótese da indução, temos que \((n-1)^2 > 6(n-1)-9=6n-15\). Assim,
\begin{equation*} n^2 > 6n-15 + 2(n-1) + 1 = 6n + 2n - 16\,, \end{equation*}e, como \(2n - 16\geq -6 > -9\) já que \(n\geq 5\), temos
\begin{equation*} n^2 > 6n+2n-16 > 6n-9\,, \end{equation*}como queríamos. □
EXERCÍCIO RESOLVIDO 2.4. Considere a seguinte tentativa de demonstração para a afirmação (equivocada): Num pacote com \(n\) jujubas, \(n\geq 1\), se uma delas é azul, então todas são azuis.
Seja \(X\) nosso pacote de \(n\) jujubas. Se \(n=1\), então é verdade que, se a única jujuba em \(X\) é azul, então todas as jujubas em \(X\) são azuis. Suponhamos, então, que \(n\geq 2\) e, por indução em \(n\), que, para todo inteiro positivo \(k < n\) e todo pacote \(P\) com \(k\) jujubas, sendo uma delas azul, temos todas as jujubas de \(P\) azuis. Supondo ainda que uma das \(n\geq 2\) jujubas em \(X\) é azul, queremos mostrar que todas as jujubas em \(X\) são azuis.
Seja \(Y\) o pacote obtido ao se remover uma jujuba azul de \(X\), a qual sabemos por hipótese que existe. Como \(Y\) tem \(n-1 < n\) jujubas, vale para \(Y\) a hipótese da indução e, portanto, temos que todas as jujubas em \(Y\) são azuis. Assim, todas as jujubas de \(X\) são azuis.
Onde está o erro nessa tentativa de demonstração?
Resolução. O erro está na conclusão de que todas as jujubas em \(Y\) são azuis. A hipótese da indução de fato nos traz a implicação "se há alguma jujuba azul em \(Y\), então todas as jujubas em \(Y\) são azuis". No entanto, não temos a garantia de que há alguma jujuba azul em \(Y\), para que possamos concluir que todas as jujubas em \(Y\) são azuis, pois pode ser que a jujuba que foi removida de \(X\) fosse a única do pacote. □
EXERCÍCIO RESOLVIDO 2.5. Considere a seguinte tentativa de demonstração para a afirmação (equivocada): Num pacote com \(n\) jujubas, \(n\geq 1\), se uma delas é azul, então todas são azuis.
Seja \(X\) nosso pacote de \(n\) jujubas. Se \(n=1\), então é verdade que, se a única jujuba em \(X\) é azul, então todas as jujubas em \(X\) são azuis. Suponhamos, então, que \(n\geq 2\) e, por indução em \(n\), que, para todo inteiro positivo \(k < n\) e todo pacote \(P\) com \(k\) jujubas, sendo uma delas azul, temos todas as jujubas de \(P\) azuis. Supondo ainda que uma das \(n\geq 2\) jujubas em \(X\) é azul, queremos mostrar que todas as jujubas em \(X\) são azuis.
Podemos supor que temos uma jujuba em \(X\) que não é azul, do contrário já teríamos a validade da afirmação. Seja \(Y\) o pacote obtido ao se remover de \(X\) uma jujuba \(z\) que não é azul, a qual sabemos por hipótese que existe. Como \(Y\) tem \(n-1 < n\) jujubas, vale para \(Y\) a hipótese da indução e, portanto, como seguramente uma das jujubas em \(Y\) é azul, temos que todas as jujubas em \(Y\) são azuis. Agora, observando que \(Y\) não é vazio, seja \(Z\) o conjunto de duas jujubas obtido tomando-se \(z\) e qualquer uma das jujubas em \(Y\). Como \(Z\) é um conjunto com pelo menos uma jujuba azul, temos que todas as jujubas em \(Z\) são azuis. Assim, \(z\) é azul e, portanto, todas as jujubas em \(X\) são azuis.
Onde está o erro nessa tentativa de demonstração?
Resolução. O erro está em aplicar a hipótese da indução sobre \(Z\). Como \(\lvert Z\rvert = 2\), não há a garantia de que \(Z\) possui menos jujubas que \(X\), uma vez que pode ser o caso de \(X\) possuir só duas jujubas. A hipótese da indução só pode ser aplicada sobre pacotes com menos jujubas que \(X\). □
Ao construirmos uma demonstração por indução, duas coisas, dentre outras, merecem nossa atenção especial:
- se as condições da hipótese da indução estão de fato sendo satisfeitas para que o passo indutivo possa ser dado, como destacado no Exercício resolvido 2.5;
- se a base da indução está sendo de fato construída de modo a ser suficiente para que a prova se sustente, como na demonstração dos Teoremas 2.6 (uma extensão do Teorema 2.1) e 2.7 a seguir.
TEOREMA 2.6. Sendo \(n\) um inteiro não-negativo qualquer, \(2^n > n\).
Tentativa de demonstração (equivocada). Seja \(n\) um inteiro não-negativo qualquer. Se \(n=0\), temos
\begin{equation*} 2^n=1 > n =0\,, \end{equation*}como queríamos. Suponhamos, então, que \(n > 0\) e, por indução em \(n\), que, para todo inteiro \(k\) satisfazendo \(0 \leq k < n\), valha que \(2^k > k\). Como \(n > 0\), temos, da definição formal de potência, que
\begin{equation} \label{eqind1a} 2^n = 2\cdot 2^{n-1} \end{equation}e, da hipótese da indução,
\begin{equation} \label{eqind2a} 2^{n-1} > n - 1\,. \end{equation}De \eqref{eqind1a} e \eqref{eqind2a}, obtemos
\begin{equation*} 2^n > 2(n-1) = (n-1)+(n-1) \end{equation*}e, como \(\underline{n-1\geq 1}\) (não é verdade),
\begin{equation*} 2^n > (n-1)+(n-1)\geq (n-1)+1=n\,, \end{equation*}como queríamos. □
Demonstração (correta). Seja \(n\) um inteiro não-negativo qualquer. Se \(n=0\), temos \(2^n=1 > n =0\), como queríamos. Se \(n=1\), temos \(2^n=2 > n =1\). Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que, para todo inteiro \(k\) satisfazendo \(0 \leq k < n\), valha que \(2^k > k\). Como \(n > 1\), temos, da definição formal de potência, que
\begin{equation} \label{eqind1b} 2^n = 2\cdot 2^{n-1} \end{equation}e, da hipótese da indução,
\begin{equation} \label{eqind2b} 2^{n-1} > n - 1\,. \end{equation}De \eqref{eqind1b} e \eqref{eqind2b}, obtemos
\begin{equation*} 2^n > 2(n-1) = (n-1)+(n-1) \end{equation*}e, como \(n-1\geq 1\),
\begin{equation*} 2^n > (n-1)+(n-1)\geq (n-1)+1=n\,, \end{equation*}como queríamos. □
TEOREMA 2.7. Qualquer valor maior que \(\,3\) pode ser obtido utilizando-se apenas notas de \(\,2\) e de \(\,5\).
Demonstração. Queremos mostrar que, para todo \(n\geq 4\), existem \(x\) e \(y\) inteiros não-negativos tais que \(n=2x+5y\). Se \(n=4\), basta tomarmos \(x=2\) e \(y=0\). Se \(n=5\), basta tomarmos \(x=0\) e \(y=1\). Suponhamos, então, que \(n\geq 6\) e, por indução, que para todo \(n'\) satisfazendo \(4\leq n' < n\) valha que existem \(x'\) e \(y'\) inteiros não-negativos tais que \(n'=2x'+5y'\). Ora, como \(n-2\) satisfaz \(4\leq n - 2 < n\), temos que existem \(a\) e \(b\) inteiros não-negativos tais que \(n-2=2a + 5b\). Assim, \(n=2(a+1)+5b\), e, tomando \(x=a+1\) e \(y=b\), temos o que queríamos. □
Observe na demonstração do Teorema 2.7 que, se tivéssemos deixado o caso \(n=5\) de fora da base da indução, não poderíamos aplicar a hipótese da indução para \(n-2\) no passo indutivo, pois não teríamos a garantia de \(n-2\geq 4\).
Na demonstração do teorema a seguir, temos um exemplo de uma demonstração por indução em \(n\) em que realmente se faz necessário enunciar a hipótese da indução para todo \(k < n\). A propósito, o jogo descrito no enunciado é o clássico Jogo de Nim para duas pilhas de pedras, da Teoria dos Jogos.
TEOREMA 2.8. Considere o seguinte jogo adversarial jogado entre dois oponentes, os quais jogam alternadamente, tendo à sua disposição duas pilhas de pedras. Em sua vez de jogar, cada jogador deve escolher uma das pilhas e remover dela qualquer número positivo de pedras. Perde o jogador que, em sua vez de jogar, não tiver escolha possível (por estarem ambas as pilhas vazias). Supondo que ambos os jogadores jogam otimamente, e sendo \(n_1\) e \(n_2\) os números de pedras na primeira e na segunda pilhas, respectivamente, o vencedor é sempre: o primeiro jogador, se \(n_1\neq n_2\); o segundo jogador, se \(n_1=n_2\).
Demonstração. Sejam Alice e Bob os nomes dos primeiro e segundo jogadores, respectivamente. Vamos primeiro mostrar que, se \(n_1=n_2=n\) e a vez de jogar é de Alice, então o vencedor é sempre Bob. Se \(n=0\), ambas as pilhas estão vazias, e Alice perde o jogo. Suponhamos, então, que \(n\geq 1\) e, por indução, que para todo inteiro não-negativo \(k < n\) e toda configuração do jogo em que ambas as pilhas possuam exatamente \(k\) pedras e a vez de jogar é de Alice, Bob é sempre o vencedor. Vamos mostrar que, para qualquer quantia positiva \(m \leq n\) de pedras que Alice escolher remover de uma das pilhas, Bob terá uma estratégia vencedora. Ora, basta que Bob remova \(m\) pedras da pilha não escolhida por Alice. Assim, teremos uma configuração do jogo com ambas as pilhas com \(n-m\) pedras, sendo a vez de jogar de Alice. Assim, como \(0\leq n - m < n\), temos, da hipótese de indução, uma estratégia vencedora para Bob para a nova configuração do jogo e, portanto, para a configuração original.
Já mostramos que, se \(n_1=n_2\), então o vencedor é sempre o jogador que não está na vez de jogar. Por outro lado, se \(n_1\neq n_2\) e a vez de jogar é de Alice, e supondo sem perda de generalidade que \(n_1 > n_2\), basta que Alice escolha remover \(n_1-n_2\) pedras da primeira pilha, deixando Bob numa configuração do jogo em que ambas as pilhas possuem igual número de pedras. Assim, retornamos ao caso anterior, e temos uma estratégia vencedora para Alice. □
O teorema a seguir provê uma fórmula fechada para o \(n\)-ésimo número de Fibonacci, denotado por \(F_n\), o qual é definido da seguinte forma:
\begin{equation*} F_n =\left\{ \begin{aligned} &n\,,&\quad&\text{se $n\leq 1$;}\\ &F_{n-1}+F_{n-2}\,,&\quad&\text{se $n\geq 2$.} \end{aligned} \right. \end{equation*}No enunciado do teorema, \(\def\upphi{\text{φ}}\upphi=(1+\sqrt 5)/2\approx 1.61803\) e \(\def\upphihat{\hat{\upphi}}\upphihat=(1-\sqrt 5)/2\approx -0.61803\) são as raízes da equação \(x^2 = x+1\).
TEOREMA 2.9. Sendo \(n\) um inteiro não-negativo qualquer,
\begin{equation*} F_n = \frac{1}{\sqrt 5}(\upphi^n - \upphihat^n)\,. \end{equation*}Demonstração. Seja \(n\) um inteiro não-negativo. Se \(n=0\),
\begin{equation*} \frac{1}{\sqrt 5}(\upphi^0 - \upphihat^0)=0=F_0\,. \end{equation*}Se \(n=1\),
\begin{align*} \frac{1}{\sqrt 5}(\upphi^1 - \upphihat^1)&= \frac{1}{\sqrt 5}\Bigl(\frac{1+\sqrt 5}2 - \frac{1-\sqrt 5}2\Bigr)\\ &= \frac{1}{\sqrt 5}\Bigl(\frac{2\sqrt 5}2\Bigr)=F_1\,.\\ \end{align*}Suponhamos então que \(n\geq 2\) e, por indução em \(n\), que para todo inteiro não-negativo \(k < n\) valha que
\begin{equation*} F_{k} = \frac{1}{\sqrt 5}\bigl(\upphi^{k} - \upphihat^{k}\bigr)\,. \end{equation*}Como \(n\geq 2\), temos por definição que
\begin{equation*} F_n=F_{n-1}+F_{n-2}\,, \end{equation*}e sabemos, da hipótese da indução, que
\begin{align*} F_{n-1} &= \frac{1}{\sqrt 5}(\upphi^{n-1} - \upphihat^{n-1})\quad\text e\\ F_{n-2} &= \frac{1}{\sqrt 5}(\upphi^{n-2} - \upphihat^{n-2})\,. \end{align*}Logo,
\begin{align*} F_n &= \frac1{\sqrt 5} \bigl(\upphi^{n-1} - \upphihat^{n-1}+\upphi^{n-2} - \upphihat^{n-2}\bigr)\\ &= \frac1{\sqrt 5} \bigl(\upphi^{n-1} +\upphi^{n-2} - (\upphihat^{n-1} + \upphihat^{n-2})\bigr)\\ &= \frac1{\sqrt 5} \bigl(\upphi^{n-2}\cdot\upphi +\upphi^{n-2}\cdot 1 - (\upphihat^{n-2}\cdot\upphihat + \upphihat^{n-2}\cdot 1)\bigr)\\ &= \frac1{\sqrt 5} \bigl(\upphi^{n-2}(\upphi + 1) - \upphihat^{n-2}(\upphihat + 1)\bigr)\\ &= \frac1{\sqrt 5} \bigl(\upphi^{n-2}(\upphi^2) - \upphihat^{n-2}(\upphihat^2)\bigr)\\ &= \frac1{\sqrt 5}(\upphi^{n} - \upphihat^{n})\,, \end{align*}como queríamos mostrar. □
Pré-lista de exercícios
- Mostre por indução que, para todo inteiro \(n\geq 5\), vale que \(2^n > n^2\).
- Mostre que qualquer valor maior que \(11\) pode ser obtido utilizando-se apenas notas de \(4\) e de \(5\).
Mostre que, para qualquer real \(x\) e quaisquer inteiros não-negativos \(n\) e \(m\), vale que \((x^n)(x^m)=x^{n+m}\).
Resolução do professor. Se \(n=0\), temos que \((x^n)(x^m)=(x^0)(x^m) = x^m= x^{n+m}\), como queríamos. Suponhamos, então, que \(n > 0\) e, por indução em \(n\), que para todo inteiro não-negativo \(k < n\) valha que \((x^{k})(x^m)=x^{k+m}\). Como \(x^n=x\cdot x^{n-1}\),
\begin{equation*} (x^n)(x^m)=(x\cdot x^{n-1})(x^m)=x(x^{n-1})(x^m)\,, \end{equation*}e como, da hipótese da indução, \((x^{n-1})(x^m)=x^{n-1+m}\), temos
\begin{equation*} (x^n)(x^m)=x(x^{n-1})(x^m)=x(x^{n-1+m}) = x^{n+m}\,, \end{equation*}como queríamos. □
Considere a afirmação: Para todo inteiro positivo \(n\), se \(x\) e \(y\) são inteiros positivos tais que \(\max(x,y)=n\), então \(x=y\). Considere também a seguinte tentativa de demonstração para essa afirmação.
Sejam \(x\) e \(y\) inteiros positivos quaisquer tais que \(\max(x,y)=n\). Se \(n=1\), como \(x\) e \(y\) são inteiros positivos e \(\max(x,y)=1\), temos que \(x=y=1\). Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que, para todo inteiro positivo \(n' < n\) e quaisquer inteiros positivos \(x'\) e \(y'\) tais que \(\max(x',y')=n'\), valha que \(x'=y'\). Ora, como \(\max(x,y)=n\), temos que \(\max(x-1,y-1)=n-1\) e, da hipótese da indução, que \(x-1=y-1\), o que implica \(x=y\).
O que está de errado com essa tentativa de demonstração?
- Sendo \(n\) um inteiro não-negativo, \(k\) um inteiro
positivo, dizemos que uma sequência de \(k\) inteiros positivos
\(b_0,\dotsc,b_{k-1}\in\{0,1\}\) é a representação canônica de \(n\) em
binário, e que \(k\) é o comprimento da representação, se \(n=\sum_{i=0}^{k-1}b_i2^i\) e: ou \(b_{k-1}=1\);
ou \(b_{k-1}=n=0\) e \(k=1\).
- Mostre que todo inteiro não-negativo \(n\) admite uma e apenas uma representação canônica em binário.
Mostre que o comprimento da representação canônica de todo inteiro positivo \(n\) em binário é igual a \(\lfloor\lg n\rfloor + 1\).
Resolução do professor. Sejam \(n\) e \(k\) inteiros positivos tais que \(n=\sum_{i=0}^{k-1}b_i2^i\) para \(b_0,\dotsc,b_{k-2}\in\{0,1\}\) e \(b_{k-1}=1\). Queremos mostrar que \(k=\lfloor\lg n\rfloor +1\).
Se \(n=1\), temos que \(n=1\cdot 2^0\) e, portanto, que \(k=1=\lfloor\lg 1\rfloor +1\), como queríamos. Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que para todo inteiro positivo \(n' < n\) valha que, se \(n' = \sum_{i=0}^{k'-1}b'_i2^i\) para \(b'_0,\dotsc,b'_{k'-2}\in\{0,1\}\) e \(b_{k'-1}=1\), então \(k'=\lfloor\lg n'\rfloor +1\).
Observando que \(n=2\sum_{i=1}^{k-1}b_i2^{i-1}+b_0\), temos dois casos.
Se \(n\) é par, então, \(b_0=0\), e podemos fazer
\begin{align*} n&=2\sum_{i=1}^{k-1}b_{i}2^{i-1}\\ &= 2\sum_{i=0}^{k-2}b_{i+1}2^{i}\,. \end{align*}Logo, \(n/2=\sum_{i=0}^{k-2}b'_{i}2^{i}\) com \(b'_i\bydef b_{i+1}\) para \(0\leq i \leq k - 2\), sendo \(b'_{k-2}=1\). Assim, da hipótese da indução,
\begin{align*} k-1 &= \Bigl\lfloor \lg{\frac n2}\Bigr\rfloor+1\\ &= \lfloor \lg n - 1\rfloor+1\\ &= \lfloor \lg n \rfloor-1+1\,, \end{align*}do que segue \(k=\lfloor \lg n\rfloor +1\), como queríamos.
Se \(n\) é ímpar, então, \(b_0=1\), e podemos fazer \(n-1=\sum_{i=0}^{k-1}b'_i2^i\) com \(b'_0\bydef 0\) e \(b'_i\bydef b_i\) para \(1\leq i\leq k - 1\). Logo, da hipótese da indução, \(k=\lfloor\lg(n - 1)\rfloor+1\), o que implica \(k-1=\lfloor\lg(n-1)\rfloor\) e, da definição da função piso,
\begin{equation*} k-1\leq \lg(n - 1) < k\,. \end{equation*}Portanto,
\begin{equation*} 2^{k-1}\leq n - 1 < 2^k\,. \end{equation*}Como \(n-1\) e \(2^k\) são ambos inteiros pares, \(n-1< 2^k-1\), e, consequentemente,
\begin{equation*} 2^{k-1}\leq n < 2^k\,, \end{equation*}o que implica \(k=\lfloor \lg n\rfloor + 1\) novamente da definição da função piso. □
O Problema do Troco (Coin Change Problem) é enunciado da seguinte maneira: dados um conjunto \(S\) de denominações de cédulas monetárias e um valor \(V\) a ser pago, qual o menor número de cédulas necessário para pagar exatamente o valor \(V\)? Por exemplo, se \(S=\{1,2,5,10\}\) e \(V=14\), o menor número de cédulas é \(3\), correspondendo a uma cédula de \(10\) e duas de \(2\). A estratégia gulosa para resolver esse problema consiste no seguinte procedimento:
- enquanto \(V > 0\):
- se toda denominação \(d\in S\) satisfaz \(d > V\), então o valor não pode ser pago;
- senão:
- tome uma cédula cuja denominação \(d\) seja a maior possível e satisfaça \(d\leq V\);
- subtraia \(d\) de \(V\).
Nem sempre é verdade que a estratégia gulosa funciona e usa o menor número possível de notas. Para \(S=\{1,5,6,9\}\) e \(V=11\), por exemplo, a estratégia gulosa usa três notas, sendo que é possível pagar o valor só com duas. Para \(S=\{2,5,6,9\}\) e \(V=10\), a estratégia gulosa nem consegue pagar o valor, sendo que é possível pagá-lo com duas notas.
- Mostre que, sendo \(k\) um inteiro positivo e \(S=\{d_1,d_2,\dotsc,d_k\}\subseteq\bZ_{> 0}\), a estratégia gulosa funciona e sempre usa o menor número possível de notas para pagar qualquer valor se \(d_i\) é múltiplo de \(d_j\) para quaisquer \(i,j\in\{1,\dotsc,k\}\) tais que \(d_j \leq d_i\).
A condição suficiente mostrada no Exercício 6.1 é também necessária para que a estratégia gulosa funcione e use sempre o menor número possível de notas para pagar qualquer valor? Justifique sua resposta.
Resolução do professor para o Exercício 6.1. Antes de apresentarmos a demonstração do teorema enunciado, vamos primeiro mostrar o seguinte lema.
LEMA. Seja \(b_1,b_2,\dotsc,b_m\), para \(\def\bN{\bZ_{\geq 0}}m\in\bN\), uma sequência de cédulas paga exatamente um dado valor \(V\) utilizando o menor número possível de cédulas em \(S\). Se \(d_1 < d_2 < \dotsb < d_k\) e \(d_i\) é múltiplo de \(d_j\) para quaisquer \(i,j\in\{1,\dotsc,k\}\) tais que \(d_j \leq d_i\), e se, para algum \(\ell\in\{1,\dotsc,k\}\), uma sequência \(b_1,\dotsc,b_m\) utiliza apenas cédulas de denominação menor que \(d_{\ell}\), então \(V < d_{\ell}\).
Demonstração. Se \(\ell=1\) ou \(V=0\), então a única possibilidade para \(b_1,\dotsc,b_m\) é a sequência vazia e, portanto, \(\sum_{j=1}^{m}b_j=V=0 < d_{\ell}\). Suponhamos, então, que \(\ell \geq 2\) e \(V > 0\). Suponhamos, por indução em \(\ell\), que, para todo inteiro positivo \(r < \ell\), valha, para toda sequência \(c_1,\dotsc,c_{m'}\) de \(m'\geq 0\) cédulas que paga exatamente um valor \(V'\) utilizando o menor número possível de cédulas em \(S\), que se \(c_1,\dotsc,c_{m'}\) utiliza apenas cédulas de denominação menor que \(d_{r}\), então \(V' < d_{r}\).
Suponhamos, sem perda de generalidade, que \(b_1\leq\dotsb\leq b_m\). Sabemos que \(m\geq 1\), já que \(V > 0\). Seja, então, \(i\) o menor inteiro positivo tal que \(b_i=b_m\), e seja também \(W\bydef \sum_{j=1}^{i-1} b_j\). Sabemos que \(b_1,\dotsc,b_{i-1}\) paga \(W\) utilizando o menor número possível de cédulas em \(S\), pois, se existisse uma sequência \(\sigma\) para pagar \(W\) com ainda menos cédulas, a concatenação de \(\sigma\) com \(b_i,\dotsc,b_m\) resultaria numa sequência com menos de \(m\) cédulas para pagar \(V\), um absurdo, já que \(b_1,\dotsc,b_m\) é uma sequência com o menor número possível de cédulas que paga \(V\). Como, da escolha de \(i\), a sequência \(b_1,\dotsc,b_{i-1}\) utiliza apenas cédulas de denominação menor que \(b_i=b_m < d_{\ell}\), a hipótese da indução nos traz que \(W < b_i\).
Como \(b_i\) divide \(d_{\ell}\) e \(b_i\neq d_{\ell}\), temos um inteiro \(t\geq 2\) tal que \(d_{\ell}=tb_i\). Da escolha de \(i\), temos que o número de ocorrências de cédulas de denominação \(b_i\) em \(b_1,\dotsc,b_m\) é \(m-i+1\), e sabemos que este número é menor que \(t\), pois, do contrário, poderíamos substituir \(t\geq 2\) ocorrências de \(b_i\) em \(b_1,\dotsc,b_m\) por uma única ocorrência de \(d_{\ell}\), obtendo uma sequência com menos de \(m\) cédulas para pagar \(V\). Destarte,
\begin{equation*} V = \sum_{j=1}^mb_j= \overbrace{\sum_{j=1}^{i-1}b_j}^{=W < b_i} + \overbrace{\sum_{j=i}^m b_j}^{=(m-i+1)b_i \leq (t-1)b_i} < b_i+(t-1)b_i = d_{\ell}\,, \end{equation*}como queríamos. □
Demonstração do teorema enunciado. Sejam \(V\in\bN\) e \(f(V)\) o número de cédulas usadas na solução ótima do problema, i.e. o número mínimo de cédulas necessárias para pagar o valor \(V\), sob a convenção de que \(f(V)=\infty\) se o valor não pode ser pago. Se \(V=0\), então a estratégia gulosa retorna que o valor pode ser pago com zero notas, o que está correto, uma vez que, neste caso, \(f(V)=0\). Suponhamos, então, que \(V > 0\), e, a fim de contradição, que, quando valem as condições do enunciado, a estratégia gulosa não funciona (i.e. retorna que o valor não pode ser pago quando, na realidade, pode o ser) ou não usa o menor número possível de notas para pagar \(V\). Note-se que, em ambos os casos, temos \(f(V) < \infty\).
Seja \(a_1,\dotsc,a_n\) a sequência de cédulas tomadas pela estratégia gulosa até retornar que o valor não pode ser pago, ou retornar que a sequência tomada paga \(V\) exatamente. Da suposição que fizemos a fim de contradição, temos que existe algum \(i\in\{1,\dotsc,n\}\) tal que, para pagar \(W\bydef V-\sum_{j=1}^{i-1}a_i\) utilizando \(f(W)\) notas, é necessário não tomar a escolha gulosa, i.e. toda sequência \(b_1,\dotsc,b_m\) que paga \(W\) com \(f(W)\) notas utiliza apenas cédulas de denominação menor que \(d_{\ell}\), sendo \(d_{\ell}\) o maior inteiro em \(S\) tal que \(d_{\ell}\leq W\). No entanto, do lema que mostramos, isso nos traz que \(W < d_{\ell}\), uma contradição. □
- enquanto \(V > 0\):
AULA 3: Mais exemplos de demonstrações sobre divisibilidade
Para provarmos que dois conjuntos \(A\) e \(B\) são iguais, temos que construir duas demonstrações, uma para mostrar que \(A\subseteq B\), e a outra para mostrar que \(B\subseteq A\).
TEOREMA 3.1. Sejam \(A\) e \(B\) os conjuntos definidos por:
\begin{align*} A &= \{ n^2 : n\text{ é um inteiro não múltiplo de $3$}\}\,;\\ B &= \{ m : m-1\text{ é múltiplo de $3$ e $m$ é um quadrado perfeito}\}\,. \end{align*}Então, \(A=B\).
Demonstração. (\(A\subseteq B\)) Seja \(x\in A\), i.e. \(x=n^2\) para algum inteiro \(n\) não múltiplo de \(3\). Vamos mostrar que \(x\in B\). Como \(n\) não é multiplo de \(3\), então existe um inteiro \(k\) para o qual vale um dos seguintes casos:
\(n=3k+1\), o que implica
\begin{equation*} n^2=(3k+1)^2=9k^2+6k+1=3(3k^2+2k)+1\,; \end{equation*}\(n=3k+2\), o que implica
\begin{equation*} n^2=(3k+2)^2=9k^2+12k+4=3(3k^2+4k+1)+1\,. \end{equation*}
Em ambos os casos, temos \(n^2=3q+1\) para um inteiro \(q\) e, portanto, \(n^2-1=3q\). Assim, \(x=n^2\) é um quadrado perfeito tal que \(x-1\) é múltiplo de \(3\); logo, \(x\in B\), como queríamos.
(\(B\subseteq A\)) Seja \(m\) um quadrado perfeito, i.e. um inteiro tal que \(m=n^2\) para algum inteiro \(n\). Por contraposição, vamos mostrar que se \(m\notin A\), então \(m\notin B\). Suponhamos, então, que \(m\notin A\), i.e. que \(n\) é um múltiplo de \(3\), i.e. existe um inteiro \(k\) tal que \(n=3k\). Queremos mostrar que \(m-1\) não é múltiplo de \(3\). Ora, \(m=n^2=9q^2=3(3q^2)\). Logo, como queríamos, \(m-1\) não é múltiplo de \(3\), pois \(m\) o é. □
TEOREMA 3.2. Todo número inteiro \(n\geq 2\) possui ao menos um fator primo.
Demonstração. Se \(n\) é primo, então \(n\) é um divisor primo de \(n\), como queríamos. Suponhamos, portanto, que \(n\) não é primo, o que implica \(n > 2\). Suponhamos também, por indução, que todo inteiro \(m\) tal que \(2\leq m < n\) possui ao menos um fator primo. Como \(n\) não é primo, existem inteiros \(a\) e \(b\) tais que \(n=ab\) com ambos \(a,b\geq 2\) e, portanto, \(a,b < n\). Assim, da hipótese da indução, \(a\) possui ao menos um fator primo \(p\), i.e. existe um inteiro \(k\) tal que \(a=pk\). Logo, \(n=pkb\), o que implica que \(p\) é também um fator primo de \(n\). □
COROLÁRIO 3.3. Seja \(n\geq 2\) um inteiro. Se para todo primo \(p < n\), temos que \(p\) não divide \(n\), então \(n\) é primo.
Demonstração. Por contraposição, suponhamos que \(n\geq 2\) não é primo. Assim, do Teorema 3.2, existe um primo \(p\) tal que \(p\) divide \(n\) e, como \(n\) não é primo, tal que \(p < n\), como queríamos. □
LEMA 3.4 (Identidade de Bézout). Sendo \(a\) e \(b\) inteiros não ambos iguais a zero, existem inteiros \(x,y\) tais que \(ax + by = \gcd(a,b)\).
Demonstração. Seja \(S=\{ax+by > 0\mathbin : x,y\in\mathbb Z\}\). Queremos mostrar que \(\gcd(a,b)\in S\). Sabemos que \(S\neq\emptyset\), pois, como \(a\) e \(b\) não são ambos zero, temos \(a\cdot a+b\cdot b > 0\), logo \(a^2+b^2\in S\). Assim, \(S\) é um conjunto não-vazio de inteiros positivos. Seja, portanto, \(d=\min S\) e sejam \(x,y\in\bZ\) tais que \(d=ax+by\). Vamos mostrar que \(d=\gcd(a,b)\).
Primeiramente, vamos mostrar que \(d\) é um divisor comum de \(a\) e \(b\). Sejam \(r\) e \(s\) são os inteiros tais que \(0\leq r,s < d\) e \(a=dk_1+r\) e \(b=dk_2+s\) para algum \(k_1\) e algum \(k_2\) inteiros. Assim,
\begin{align*} r &= a - dk_1 = a - (ax+by)k_1 = a(1-xk_1)+b(-yk_1)\\ \text e\quad s &= b - dk_2 = b - (ax + by)k_2 = a(-xk_2)+b(1-yk_2)\,. \end{align*}Logo, \(r,s\in S\cup\{0\}\). Como tanto \(r\) quanto \(s\) são estritamente menores que \(d=\min S\), temos \(r=s=0\), o que implica \(a=dk_1\) e \(b=dk_2\), i.e. \(d\) é um divisor comum de \(a\) e \(b\).
Vamos agora mostrar que todo divisor comum de \(a\) e \(b\) é um divisor de \(d\), para concluirmos que \(d=gcd(a,b)\). Seja \(c\) um divisor comum de \(a\) e \(b\) e sejam \(q_1,q_2\) inteiros tais que \(a=cq_1\) e \(b=cq_2\). Assim,
\begin{align*} d&=ax+by\\ &=cq_1x+cq_2y\\ &=c(q_1x+q_2y)\,. \end{align*}Logo, \(c\) divide \(d\), como queríamos. □
LEMA 3.5 (Lema de Euclides). Para quaisquer inteiros \(a\) e \(b\), todo divisor primo do produto \(ab\) é também um divisor de \(a\) ou de \(b\) (ou de ambos).
Demonstração. Seja \(p\) um número primo que divide \(ab\). Vamos mostrar que, se \(p\) não divide \(a\), então \(p\) divide \(b\). Suponhamos, então, que \(p\) não divide \(a\). Como \(\gcd(a,p)=1\), temos, da Identidade de Bézout, que existem \(x,y\in\bZ\) tais que
\begin{equation*} ax+py=1 \end{equation*}e, portanto,
\begin{equation*} abx+pby=b\,. \end{equation*}Como \(ab=pk\) para algum inteiro \(k\), temos
\begin{equation*} p(kx+by)=b\,. \end{equation*}Portanto, \(p\) divide \(b\). □
TEOREMA 3.6 (Teorema de Euclides). Existem infinitos números primos.
Demonstração. Suponhamos, a fim de contradição, que \(p_1,p_2,\dotsc, p_n\) sejam todos os números primos que existem, para algum inteiro positivo \(n\), e tomemos \(P\) o produto destes números. Do Exercício 6, sabemos que \(P\) e \(P+1\) são inteiros coprimos, o que implica que nenhum dos números \(p_1,p_2,\dotsc, p_n\) é um divisor de \(P+1\). Logo, como supusemos que \(p_1,p_2,\dotsc,p_n\) são todos os números primos que existem, não há número primo algum estritamente menor que \(P+1\) que seja um divisor de \(P+1\), o que implica, do Corolário 3.3, que \(P+1\) é também um número primo, uma contradição. □
LEMA 3.7. Seja \(\ell\) um inteiro positivo. Se \(p,q_1,\dotsc,q_{\ell}\) são todos números primos e \(p\) divide o produto \(q_1\dotsb q_{\ell}\), então existe algum inteiro \(i\) satisfazendo \(1\leq i\leq \ell\) tal que \(p=q_i\).
Demonstração. Se \(\ell=1\), então \(p\) divide \(q_1\), o que implica \(p=q_1\) da primalidade de ambos \(p,q_1\). Suponhamos, então, que \(\ell\geq 2\) e, por indução em \(\ell\), que para todo \(k < \ell\) e todo conjunto de \(k\) números primos \(q'_1,\dotsc,q'_k\) tais que \(p\) divida o produto \(q'_1\dotsb q'_k\), temos que \(p\) é um dos primos \(q'_1,\dotsc,q'_k\). Ora, como \(p\) divide o produto \(q_1\dotsb q_{\ell}\), temos duas possibilidades:
\(p\) divide \(q_1\)
Neste caso, da primalidade de ambos \(p,q_1\), temos \(p=q_1\), como queríamos.
\(p\) não divide \(q_1\)
Neste caso, do Lema de Euclides, temos, já que \(\ell\geq 2\), que \(p\) divide o produto \(q_2\dotsb q_{\ell}\) e, da hipótese da indução, que \(p\) é um dos primos \(q_2,\dotsc,q_{\ell}\), como queríamos. □
TEOREMA 3.8 (Teorema Fundamental da Aritmética). Todo número inteiro \(n \geq 2\) pode ser escrito de modo único como o produto de números primos, a menos da ordem dos fatores.
Demonstração. (Existência) Vamos mostrar que todo inteiro \(n\geq 2\) pode ser escrito como o produto de números primos. Se \(n\) é primo, a afirmação se verifica imediatamente, inclusive quando \(n=2\). Suponhamos, então, que \(n > 2\) não é primo e, por indução em \(n\), que todo inteiro em \(\{2,\dotsc, n-1\}\) pode ser escrito como o produto de números primos. Ora, como \(n\) não é primo, existem dois inteiros \(a\) e \(b\) satisfazendo \(1 < a,b < n\) tais que \(n=ab\). Como \(a\) e \(b\) são menores que \(n\), da hipótese da indução temos que \(a= p_1p_2\dotsb p_k\) e \(b=q_1q_2\dotsb q_{\ell}\), sendo \(p_1,p_2,\dotsc,p_k\) e \(q_1,q_2,\dotsc,q_{\ell}\) todos números primos. Assim,
\begin{equation*} n = p_1p_2\dotsb p_kq_1q_2\dotsb q_{\ell}\,, \end{equation*}como queríamos.
(Unicidade) Vamos mostrar que, para todo inteiro \(n\geq 2\), é único, a menos da ordem dos fatores, o produto de números primos que é igual a \(n\). A fim de contradição, tomemos o menor inteiro \(n\geq 2\) para o qual
\begin{equation*} n= p_1p_2\dotsb p_k=q_1q_2\dotsb q_{\ell}\,, \end{equation*}sendo \(p_1,p_2,\dotsc,p_k\) e \(q_1,q_2,\dotsc,q_{\ell}\) todos números primos, de modo que o produto \(q_1q_2\dotsb q_{\ell}\) não possa ser obtido apenas permutando-se os fatores em \(p_1p_2\dotsb p_k\), o que implica que ambos os produtos possuem ao menos dois fatores e, portanto, que \(n\) não é primo. Assim, como \(p_1\) divide \(q_1q_2\dotsb q_{\ell}\), então, do Lema 3.7, \(p_1=q_i\) para algum \(i\) satisfazendo \(1\leq i\leq \ell\). Supondo sem perda de generalidade que \(i=1\), e como \(k\geq 2\) e \(\ell\geq 2\), temos
\begin{equation*} 2\leq m\bydef p_2\dotsb p_k=q_2\dotsb q_{\ell} < n\,, \end{equation*}de modo que \(q_2\dotsb q_{\ell}\) não pode ser obtido apenas permutando-se os fatores em \(p_2\dotsb p_k\), contrariando a minimalidade da escolha de \(n\). □
Leitura complementar: o Teorema de Euclides–Euler
O teorema a seguir relaciona os primos de Mersenne com os números perfeitos pares. Este teorema é um exemplo muito interessante de uma equivalência. A necessidade foi mostrada por Euclides, mas a suficiência foi mostrada apenas dois mil anos depois, por Euler. Para facilitar a demonstração, vamos utilizar \(\sigma(n)\) para denotar a soma dos divisores de \(n\), sendo \(n\) qualquer inteiro não-negativo (por exemplo, \(\sigma(6)=12\)).
TEOREMA 3.9 (Teorema de Euclides–Euler). Um número natural \(n\) é um número perfeito par se e somente se \(n=2^{p-1}(2^p-1)\) para algum número primo de Mersenne \(2^p-1\).
Demonstração. (Necessidade) Vamos mostrar que se \(2^p-1\) é um primo de Mersenne, então \(2^{p-1}(2^p-1)\) é um número perfeito par. Seja, então, \(p\) um número primo tal que \(2^p-1\) também é um número primo. Sabemos que \(2^{p-1}(2^p-1)\) é um número par, uma vez que \(p\geq 2\) implica \(2^{p-1}\geq 2\). Resta mostrar que \(2^{p-1}(2^p-1)\) é um número perfeito, isto é, que \(\sigma(2^{p-1}(2^p-1))=2\times(2^{p-1}(2^p-1))=2^p(2^p-1)\). Ora, como \(2^p-1\) é primo, os únicos fatores primos de \(2^{p-1}(2^p-1)\) são \(2\) e \(2^p-1\). Logo, todo divisor de \(2^{p-1}(2^p-1)\) só pode ser da forma \(2^i\) ou \(2^i(2^p-1)\) para algum \(i\in\{0,\dotsc,p-1\}\). Portanto,
\begin{align*} \sigma(2^{p-1}(2^p-1))&=\sum_{i=0}^{p-1}\bigl(2^i+2^i(2^p-1)\bigr)\\ &=\sum_{i=0}^{p-1}2^i + (2^p-1)\sum_{i=0}^{p-1}2^i\\ &=2^p-1+(2^p-1)(2^p-1)\\ &=(2^p-1)(1 + (2^p-1))\\ &=2^p(2^p-1)\,, \end{align*}como queríamos.
(Suficiência) Seja \(n\) um número perfeito par, isto é, um número par tal que \(\sigma(n)=2n\). Queremos mostrar que \(n=2^{p-1}(2^p-1)\) para algum primo de Mersenne \(2^p-1\). Ora, como \(n\) é par, então existem algum inteiro positivo \(k\) e algum inteiro ímpar \(m\) tais que
\begin{equation} \label{eqn2km} n=2^km\,. \end{equation}Como \(2^k\) e \(m\) são coprimos, temos do Exercício 18 que
\begin{equation} \sigma(n)=\sigma(2^k)\sigma(m)\,, \end{equation}o que implica, como \(\sigma(n)=2n\) e \(\sigma(2^k)=2^{k+1}-1\),
\begin{equation} \label{eq2n} 2n=(2^{k+1}-1)\sigma(m)\,. \end{equation}Combinando \eqref{eqn2km} com \eqref{eq2n}, ficamos com
\begin{equation} \label{eqm2k} 2^{k+1}m={(2^{k+1}-1)\sigma(m)}\,, \end{equation}o que significa que \(2^{k+1}\) divide \(\sigma(m)\), já que não divide \(2^{k+1}-1\) (cf. Exercício 14). Logo, \(m'\bydef\sigma(m)/(2^{k+1})\) é um inteiro, e podemos re-escrever \eqref{eqm2k} como
\begin{equation} \label{eqm2kdiv} m=(2^{k+1}-1)m'\,, \end{equation}o que implica
\begin{equation} \label{eqm2kprime} m+m'=2^{k+1}m'\,. \end{equation}Como \(m'=\sigma(m)/(2^{k+1})\) por definição, temos que \(\sigma(m)=2^{k+1}m'\), e como \(m\) e \(m'\) são divisores de \(m\) (por \eqref{eqm2kdiv}), temos que \(m+m'\leq\sigma(m)\). Logo, por \eqref{eqm2kprime},
\begin{equation*} m+m'=2^{k+1}m'\leq\sigma(m) =2^{k+1}m'\,, \end{equation*}e, consequentemente, \(\sigma(m)=m+m'\), o que só é possível se \(m\) e \(m'\) forem os únicos divisores de \(m\) e se \(m'=1\), isto é, se \(m\) for primo. Como \(m'=1\) implica \(m=2^{k+1}-1\) por \eqref{eqm2kdiv}, temos que \(m\) é um primo de Mersenne (e, portanto, do Exercício 16, que \(k+1\) é um número primo) e, por \eqref{eqn2km}, que \(n=2^k(2^{k+1}-1)\), como queríamos provar. □
Pré-lista de exercícios
- Mostre, para todo inteiro \(n\geq 2\), que se \(n\) não é primo, então \(n\) possui um divisor \(d\) tal que \(1 < d\leq\sqrt n\).
Mostre a seguinte versão do enunciado da Identidade de Bézout, um pouco mais forte que a do enunciado do Lema 3.4: Sendo \(a,b,c\) inteiros, com não ambos \(a,b\) iguais a zero, existem inteiros \(x,y\) tais que \(ax+by=c\) se e somente se \(c\) é múltiplo de \(\gcd(a,b)\).
Demonstração. (Suficiência) Sejam \(x,y\) inteiros tais que \(ax+by=c\). Vamos mostrar que \(c\) é múltiplo de \(\gcd(a,b)\fedyb d\). Como \(d\) divide ambos \(a,b\), sejam \(k_1,k_2\) inteiros tais que \(a=dk_1\) e \(b=dk_2\). Assim,
\begin{align*} c&=ax+by\\ &= dk_1x+dk_2y\\ &= d(k_1x+k_2y)\,. \end{align*}Portanto, \(d\) é um divisor de \(c\), como queríamos.
(Necessidade) Seja \(c\) um múltiplo de \(\gcd(a,b)\fedyb d\) e seja \(k\in\bZ\) tal que \(c=dk\). Como, do Lema 3.4, temos que existem \(x,y\in\bZ\) tais que \(ax+by=d\), temos que
\begin{align*} c = dk &= (ax+by)k\\ &= a(xk)+b(yk)\,, \end{align*}como queríamos. □
AULA 4: Relações, funções, e operações
Um conceito muito importante quando lidamos com conjuntos quaisquer (não apenas conjuntos numéricos) é o conceito de relação.
DEFINIÇÃO 4.1. Sendo \(A\) e \(B\) dois conjuntos quaisquer, uma relação binária \(R\) de \(A\) para \(B\) é um subconjunto de \(A\times B\). Ainda, dizemos que \(A\) é o conjunto de partida de \(R\) e que \(B\) é o conjunto de chegada, ou contradomínio, de \(R\). Se \((a,b)\in R\) para algum \(a\in A\) e algum \(b\in B\), dizemos que \(a\) é relacionado a \(b\) por \(R\), e escrevemos \(aRb\). A imagem de um \(a\in A\) por \(R\), denotada por \(R(a)\), é o conjunto \(\{b\in B\mathbin : aRb\}\). A imagem inversa de um \(b\in B\) por \(R\), denotada por \(R^{-1}(b)\), é o conjunto \(\{a\in A\mathbin : aRb\}\). Sendo \(X\subseteq A\) e \(Y\subseteq B\), podemos falar também da imagem de \(X\) por \(R\) e da imagem inversa de \(Y\) por \(R\), definidas e denotadas por
\begin{align*} R(X)&\bydef\bigcup_{a\in X}R(a)\quad\text e\\ R^{-1}(Y)&\bydef\bigcup_{b\in Y}R^{-1}(b)\,, \end{align*}respectivamente. Chamamos de domínio de \(R\) o conjunto
\begin{equation*} \{a\in A\mathbin : \exists b\in B(aRb)\}= \{a\in A\mathbin : R(a)\neq\emptyset\}=R^{-1}(B)\,, \end{equation*}assim como de imagem de \(R\) o conjunto
\begin{equation*} \{b\in B\mathbin : \exists a\in A(aRb)\}= \{b\in B\mathbin : R^{-1}(b)\neq\emptyset\}=R(A)\,. \end{equation*}Por fim, a relação inversa de \(R\), denotada por \(R^{-1}\), é a relação de \(B\) para \(A\) tal que \(bR^{-1}a\) se e somente se \(aRb\).
Como exemplo, considere a relação \(R\) de \(A=\{0,1,2,3,4,5\}\) para \(B=\{2,3,4,5,6,7\}\) tal que \(xRy\) se e somente se \(x+y\) é um número primo.
- A imagem de \(2\) por \(R\) é o conjunto \(R(2)=\{3,5\}\).
- A imagem inversa de \(6\) por \(R\) é o conjunto \(R^{-1}(6)=\{1,5\}\).
- A imagem de \(\{0,1\}\) por \(R\) é o conjunto \(R(\{0,1\})=\{2,3,4,5,6,7\}\).
- A imagem inversa de \(\{2,3\}\) por \(R\) é o conjunto \(R^{-1}(\{2,3\})=\{0,1,2,3,4,5\}\).
- O domínio de \(R\) é todo o conjunto \(A\).
- A imagem de \(R\) é todo o conjunto \(B\).
Sendo \(A\), \(B\), e \(C\) conjuntos, e sendo \(R\) uma relação de \(A\) para \(B\) e \(S\) uma relação de \(B\) para \(C\), usamos \(R\circ S\) para denotar a composição das relações \(R\) e \(S\), isto é, a relação tal que, para todo \(a\in A\) e todo \(c\in C\), vale que \(a(R\circ S)c\) se e somente se existe algum \(b\in B\) tal que \(aRb\) e \(bSc\).
DEFINIÇÃO 4.2. Uma endorrelação, ou autorrelação, sobre um conjunto \(A\), é uma relação binária de \(A\) para \(A\).
Por vezes, quando dizemos "uma relação binária sobre um conjunto \(A\)", estamos nos referindo a uma autorrelação sobre \(A\).
Sendo \(A\) um conjunto, um exemplo de autorrelação sobre \(A\) é a autorrelação identidade, isto é, a autorrelação \(i_A\) tal que \(ai_Ab\) se e somente se \(a=b\). Deste modo, sendo \(R\) uma autorrelação qualquer sobre \(A\) e \(k\in\def\bN{\bZ_{\geq 0}}\bN\), a \(k\)-ésima potência de \(R\) é a composição de \(R\) com \(R\) iterada com \(k\) termos, isto é,
\begin{equation*} R^k=\overbrace{R\circ R\circ\dotsb\circ R}^{\text{$k$ $R$'s}}\,, \end{equation*}a qual pode ser definida formalmente como
\begin{equation*} R^k\bydef\left\{ \begin{aligned} &i_A\,,&&\text{se $k=0$;}\\ &R\circ R^{k-1}\,,&&\text{se $k>0$.}\\ \end{aligned} \right. \end{equation*}DEFINIÇÃO 4.3. Uma relação binária \(R\) sobre um conjunto \(A\) é dita:
- reflexiva se, para todo \(a\) em \(A\), vale que \(aRa\);
- simétrica se, para todo \(a\) e todo \(b\) em \(A\), vale que se \(aRb\), então \(bRa\);
- antissimétrica se, para todo \(a\) e todo \(b\) em \(A\), vale que se \(aRb\) e \(bRa\), então \(a=b\);
- transitiva se, para todo \(a\), todo \(b\), e todo \(c\) em \(A\), vale que se \(aRb\) e \(bRc\), então \(aRc\).
Alguns casos especiais de relação binária trabalhados nesta aula:
DEFINIÇÃO 4.4. Uma relação de equivalência \(R\) sobre um conjunto \(A\) é uma relação binária sobre \(A\) que é reflexiva, simétrica, e transitiva. Para todo \(a\in A\), a classe de equivalência de \(a\) pela relação \(R\) é o conjunto \([a]_R\bydef\{b\in A\mathbin : aRb\}\). O conjunto quociente de \(A\) por \(R\), denotado por \(A/R\), é o conjunto das classes de equivalência dos elementos de \(A\) por \(R\), isto é, \(A/R\bydef\{[a]_R\mathbin : a\in A\}\).
Como exemplo de uma relação de equivalência sobre \(\bZ\), considere a relação de congruência módulo um dado inteiro positivo \(n\). Dizemos que dois inteiros \(a\) e \(b\) são congruentes módulo \(n\), e escrevemos \(a\equiv b\pmod n\), se \(n\) divide \(a-b\). Por exemplos,
\begin{align*} 7&\equiv 2&&\pmod5\,,\\ 1&\equiv 11&&\pmod5\,,\\ -4&\equiv 1&&\pmod 5\,. \end{align*}Veja que esta relação é uma relação de equivalência sobre \(\bZ\), pois:
- é reflexiva, uma vez que, para todo \(a\in\bZ\), temos \(a\equiv a\pmod n\), pois \(a-a=n\cdot 0\) (logo, \(n\) divide \(a-a\));
é simétrica, uma vez que, para quaisquer \(a,b\in\bZ\), temos
\begin{equation*} (a\equiv b\pmod n)\Rightarrow( b\equiv a\pmod n)\,, \end{equation*}pois se \(a-b=n\cdot k\) para algum \(k\in\bZ\) (i.e. se \(n\) divide \(a-b\)), então \(b-a=n\cdot(-k)\) (logo, \(n\) divide \(b-a\));
é transitiva, uma vez que, para quaisquer \(a,b,c\in\bZ\), temos
\begin{equation*} (a\equiv b\pmod n)\wedge(b\equiv c\pmod n) \Rightarrow (a\equiv c\pmod n)\,, \end{equation*}pois se \(a-b=n\cdot k_1\) para algum \(k_1\in\bZ\) (i.e. se \(n\) divide \(a-b\)) e se \(b-c = n\cdot k_2\) para algum \(k_2\in\bZ\) (i.e. se \(n\) divide \(b-c\)), então \(a-c=n\cdot(k_1+k_2)\) (logo, \(n\) divide \(a-c\)).
O conjunto quociente de \(\bZ\) pela relação de congruência módulo \(n\) é frequentemente denotado por \(\bZ_n\) na literatura, sendo a classe de equivalência de um inteiro \(a\) denotada por \([a]_n\).
DEFINIÇÃO 4.5. Sendo \(A\) um conjunto, dizemos que uma família \(\mathscr F\) de subconjuntos não-vazios de \(A\) é uma partição de \(A\) se os subconjuntos em \(\mathscr F\) são dois a dois disjuntos e se \(\bigcup_{X\in \mathscr F}X=A\).
TEOREMA 4.6. O conjunto quociente de um conjunto \(A\) por uma relação de equivalência \(R\) é uma partição de \(A\).
Demonstração. Seja \(R\) uma relação de equivalência sobre um conjunto \(A\). Vamos mostrar que \(A/R\) é uma partição de \(A\). Como cada elemento de \(A/R\) é a classe de equivalência \([a]_R\) para algum \(a\in A\), sabemos que cada elemento de \(A/R\) é um subconjunto de \(A\). Precisamos, então, mostrar que:
- cada elemento de \(A/R\) é não-vazio;
- os elementos de \(A/R\) são dois a dois disjuntos;
- \(\bigcup_{X\in A/R}X=A\).
Vamos mostrar que cada elemento de \(A/R\) é não-vazio, isto é, vamos mostrar que \([a]_R\neq\emptyset\) para todo \(a\in A\). Ora, temos para todo \(a\in A\) que \(aRa\) da reflexividade de \(R\), o que nos traz que \(a\in [a]_R\) e, portanto, que \([a]_R\neq\emptyset\).
Agora, vamos mostrar que os elementos de \(A/R\) são dois a dois disjuntos, isto é, vamos mostrar que, para quaisquer \(a,b\in A\), se \([a]_R\neq [b]_R\), então \([a]_R\cap [b]_R=\emptyset\). Sejam \(a\) e \(b\) elementos de \(A\) e, por contraposição, suponhamos que \([a]_R\cap [b]_R\neq\emptyset\) para mostrarmos que \([a]_R=[b]_R\). Como supusemos \([a]_R\cap [b]_R\neq\emptyset\), podemos tomar um elemento \(c\in [a]_R\cap [b]_R\), o que implica tanto \(aRc\) e \(bRc\) quanto \(cRa\) e \(cRb\), pela simetria de \(R\). Vamos mostrar que \([a]_R\subseteq [b]_R\) e que \([b]_R\subseteq [a]_R\):
- Seja \(x\in [a]_R\). Como \(xRa\) e \(aRc\), temos \(xRc\) pela transitividade de \(R\). Como ainda \(cRb\), temos \(xRb\) novamente pela transitividade de \(R\). Portanto, \(x\in [b]_R\), e isto prova \([a]_R\subseteq [b]_R\).
- Seja \(y\in [b]_R\). Como \(yRb\) e \(bRc\), temos \(yRc\) pela transitividade de \(R\). Como ainda \(cRa\), temos \(yRa\) novamente pela transitividade de \(R\). Portanto, \(y\in [a]_R\), e isto prova \([b]_R\subseteq [a]_R\).
Por fim, vamos mostrar que \(\bigcup_{X\in A/R}X=A\), isto é, que \(\bigcup_{a\in A}[a]_R=A\). Sabemos que, para todo \(a\in A\), todo elemento de \([a]_R\) é também um elemento de \(A\), o que implica \(\bigcup_{a\in A}[a]_R\subseteq A\). Por outro lado, para todo \(a\in A\), sabemos que \(a\in [a]_R\) da reflexividade de \(R\), o que implica \(A\subseteq \bigcup_{a\in A}[a]_R\), concluindo a demonstração. □
No exemplo da relação de congruência módulo um inteiro positivo \(n\), temos
\begin{equation*} \bZ_n =\{[0]_n,[1]_n,\dotsc,[n-1]_n\}\,. \end{equation*}No caso particular de \(n=3\), temos
\begin{align*} \bZ_3&=\{[0]_3,[1]_3,[2]_3\}\\ &=\{\{\dotsc,-6,-3,0,3,6,\dotsc\},\{\dotsc,-5,-2,1,4,7,\dotsc\},\{\dotsc,-4,-1,2,5,8,\dotsc\}\}\,. \end{align*}DEFINIÇÃO 4.7. Uma relação de ordem parcial sobre um conjunto \(A\) é uma relação binária \(\preceq\) sobre \(A\) que é reflexiva, antissimétrica, e transitiva. Se ainda, para quaisquer \(a,b\in A\) vale que \(a\preceq b\) ou \(b\preceq a\), também dizemos que a relação é uma relação de ordem total.
Sendo \(S\) o conjunto de todos os subconjuntos de um conjunto \(A\), a relação \(\subseteq\) é um exemplo de uma relação de ordem parcial sobre \(S\), pois:
- é reflexiva, uma vez que para todo \(X\in S\) vale que \(X\subseteq X\);
- é antissimétrica, uma vez que para quaisquer \(X,Y\in S\) vale que se \(X\subseteq Y\) e \(Y\subseteq X\), então \(X=Y\);
- é transitiva, uma vez que para quaisquer \(X,Y,Z\in S\) vale que se \(X\subseteq Y\) e \(Y\subseteq Z\), então \(X\subseteq Z\).
Observe-se que, caso \(A\) possua pelo menos dois elementos, a relação \(\subseteq\) não é uma relação de ordem total, uma vez que para quaisquer elementos distintos \(a\) e \(b\) de \(A\) temos tanto \(\{a\}\not\subseteq\{b\}\) quanto \(\{b\}\not\subseteq\{a\}\).
DEFINIÇÃO 4.8. Sendo \( A \) e \( B \) conjuntos quaisquer, dizemos que uma relação binária \(f\) de \(A\) para \(B\) é uma função de \(A\) para \(B\) (ou de \(A\) em \(B\)), e escrevemos \(f\colon A\to B\), se para todo \(a\in A\), o conjunto \(f(a)\) possui exatamente um elemento, situação em que abusamos da notação \(f(a)\) para denotar o único elemento desse conjunto. Ainda, se \(f(x)=f(y)\) implica \(x=y\) para quaisquer \(x,y\in A\), então dizemos que \(f\) é injetiva (ou uma injeção de \(A\) em \(B\)). Se \(f(A)=B\), dizemos que \(f\) é sobrejetiva (ou uma sobrejeção de \(A\) em \(B\)). Por fim, dizemos que \(f\) é bijetiva (ou uma bijeção entre \(A\) e \(B\), ou uma correspondência biunívoca entre \(A\) e \(B\)) se \(f\) é injetiva e sobrejetiva.
Sejam \(A\) e \(B\) conjuntos, \(f\colon A\to B\) uma função, e \(y\in B\). No caso particular em que o conjunto \(f^{-1}(y)\) possui um único elemento, costumamos abusar da notação \(f^{-1}(y)\) para denotar o único elemento desse conjunto.
DEFINIÇÃO 4.9. Uma operação binária, ou simplesmente operação, sobre um conjunto \(X\) é uma função \(\Delta\colon X^2 \to X\). Sendo \(x,y\in X\), usamos \(x\Delta y\) para denotar \(\Delta(x,y)\).
Como exemplo de operações sobre \(\bZ_n\), sendo \(n\) um inteiro positivo, temos as operações \(+\) e \(\cdot\) da aritmética modular definidas por:
\begin{equation*} \begin{aligned} {[}a{]}_n+[b]_n &\bydef [a+b]_n\,,\\ [ a ]_n\cdot[b]_n &\bydef [ab]_n\,, \end{aligned}\quad\forall a,b\in\bZ\,. \end{equation*}Em particular,
\begin{align*} [2]_4+[5]_4&=[3]_4\quad\text e\\ [2]_5\cdot [3]_5&=[1]_5\,. \end{align*}Pré-lista de exercícios
Sejam:
- \(A\) o conjunto de todos os números ímpares menores que \(24\);
- \(B=\{ 3(k+1) \mathbin : k\text{ é um inteiro positivo}\}\);
- \(C\) o conjunto de todos os números primos menores que \(24\).
Mostre que \((A\cup\{1,2\})\setminus B=C\).
Mostre, para quaisquer subconjuntos \(A,B,C\) de um conjunto \(S\) qualquer, que
\begin{equation*} \bigl((A\cup B)\cap C \bigr)\cup \bigl((A\cup B)\cap(S\setminus C)\bigr) = A\cup B\,. \end{equation*}- Considere a relação binária \(R\) sobre \(\{a,b\}\) dada por
\(R=\{(a,b),(b,a)\}\).
- \(R\) é reflexiva?
- \(R\) é simétrica?
- \(R\) é antissimétrica?
- \(R\) é transitiva?
- Considere a autorrelação \(R\) sobre \(\{0,1,2,3,4,5,6,7,8,9,10\}\) tal
que \(xRy\) se e somente se \(x+y\) é um quadrado perfeito.
- Qual a imagem de \(0\) por \(R\)?
- Qual a imagem inversa de \(10\) por \(R\)?
- Qual a imagem de \(\{1,2,3\}\) por \(R\)?
- Qual a imagem inversa de \(\{8,9\}\) por \(R\)?
- Qual o domínio de \(R\)?
- Qual a imagem de \(R\)?
- Quais são todas as partições do conjunto \(\{1,2,3\}\)?
- Mostre que se existe injeção de um conjunto \(A\neq\emptyset\) para um conjunto \(B\), então existe uma sobrejeção de \(B\) para \(A\).
- Seja \(A\) um conjunto finito e \(\mathcal S\) o conjunto de todos os subconjuntos
de \(A\). Seja ainda \(R\) a relação binária sobre \(\mathcal S\) definida
por: \(XRY\) se e somente se existe injeção de \(X\) em \(Y\).
- \(R\) é uma relação de ordem parcial? Por quê?
- Se \(\mathcal S\) não fosse o conjunto de todos os subconjuntos de \(A\), mas um conjunto não-vazio de alguns subconjuntos de \(A\) de modo que, para quaisquer \(X,Y\in\mathcal S\), fosse verdade que \(\lvert X\rvert\neq\lvert Y\rvert\), então \(R\) seria uma relação de ordem parcial? E uma relação de ordem total? Por quê?
- Sejam agora \(A\) um conjunto qualquer, não necessariamente finito, \(\mathcal S\) o conjunto de todos os subconjuntos de \(A\), e \(R\) a relação binária sobre \(\mathcal S\) definida por: \(XRY\) se e somente se existe bijeção de \(X\) em \(Y\). É verdade que \(R\) é uma relação de equivalência? Por quê?
Seja \(n\) um inteiro positivo, seja \({\mathscr M}_n\) o conjunto de todas as matrizes quadradas \(n\times n\) sobre \(\bR\), e seja \(\mathsf X\in{\mathscr M}_n\). Seja ainda \(R_{\mathsf X}\) a relação binária sobre \({\mathscr M}_n\) tal que \(\mathsf AR_{\mathsf X}\mathsf B\) se e somente se \(\mathsf{AX}=\mathsf{XB}\). Qual a condição suficiente e necessária sobre \(\mathsf X\) para que \(R_{\mathsf X}\) seja uma relação de equivalência? Prove a suficiência e a necessidade da condição apresentada.
Resolução do professor. A condição é a enunciada no teorema a seguir.
TEOREMA. Seja \(\mathsf X\in{\mathscr M}_n\). A relação \(R_{\mathsf X}\) sobre \({\mathscr M}_n\) é uma relação de equivalência se e somente se \(\mathsf X=\alpha {\def\idtty{\mathbb 1}\idtty}_n\) para algum \(\alpha\in \bR\) qualquer.
Antes de apresentar a demonstração para o teorema, vamos apresentar um lema.
LEMA. Seja \(\mathsf X\in{\mathscr M}_n\). A relação \(R_{\mathsf X}\) sobre \({\mathscr M}_n\) é uma relação de equivalência se e somente se \(R_{\mathsf X}\) é reflexiva.
Demonstração. (Suficiência) Se \(R_{\mathsf X}\) é uma relação de equivalência, então \(R_{\mathsf X}\) é reflexiva por definição.
(Necessidade) Suponhamos que \(R_{\mathsf X}\) seja reflexiva. Então,
- Para quaisquer \(\mathsf A,\mathsf B\in{\mathscr M}_n\), se \(\mathsf {AX}=\mathsf {XB}\), então, como \(\mathsf{XB}=\mathsf{BX}\) e \(\mathsf{AX}=\mathsf{XA}\), temos \(\mathsf{BX}=\mathsf{XA}\); portanto, \(R_{\mathsf X}\) é simétrica.
- Para quaisquer \(\mathsf A,\mathsf B,\mathsf C\in{\mathscr M}_n\), se \(\mathsf{AX}=\mathsf{XB}\) e \(\mathsf{BX}=\mathsf{XC}\), então, como \(\mathsf{XB}=\mathsf{BX}\), temos \(\mathsf{AX}=\mathsf{XC}\); portanto, \(R_{\mathsf X}\) é transitiva. □
Demonstração do teorema. Tendo em vista o lema, basta mostrar que \(R_{\mathsf X}\) é uma relação reflexiva se e somente se \(\mathsf X=\alpha \idtty_n\) para algum \(\alpha\in \bR\) qualquer.
(Suficiência) Suponhamos que \(R_{\mathsf X}\) seja uma relação reflexiva. Queremos mostrar que \(\mathsf X=\alpha \idtty_n\) para algum \(\alpha\in \bR\).
Primeiramente, vamos mostrar que \(\mathsf X=\DeclareMathOperator{\diag}{diag}\diag(x_{11},x_{22},\dotsc,x_{nn})\), para \(x_{11},x_{22},\dotsc,x_{nn}\in\bR\). Para tanto, sendo \(k\) um inteiro qualquer em \(\{1,\dotsc,n\}\), vamos mostrar que \(x_{kj}=0\) para todo \(j\in\{1,\dotsc,n\}\setminus\{k\}\). Seja \(\mathsf C=(c_{ij})\in\mathscr M_n\) a matriz definida por: \(c_{ij}=1\), se \(i=j=k\); \(c_{ij}=0\), caso contrário. Observemos que a \(k\)-ésima linha de \(\mathsf{CX}\) é igual à \(k\)-ésima linha de \(\mathsf X\), enquanto que, na \(k\)-ésima coluna de \(\mathsf{CX}\), todos os elementos fora da diagonal principal são iguais a zero. Por outro lado, a \(k\)-ésima coluna de \(\mathsf{XC}\) é igual à \(k\)-ésima coluna de \(\mathsf X\), enquanto que, na \(k\)-ésima linha de \(\mathsf{XC}\), todos os elementos fora da diagonal principal são iguais a zero. Assim, como \(\mathsf{CX}=\mathsf{XC}\), podemos concluir que a \(k\)-ésima linha e a \(k\)-ésima coluna de \(\mathsf X\) são, respectivamente, iguais à \(k\)-ésima linha e a \(k\)-ésima coluna de \(\mathsf{CX}\). Portanto, \(x_{kj}=0\) para todo \(j\in\{1,\dotsc,n\}\setminus\{k\}\), como queríamos.
Vamos agora mostrar que \(\mathsf X=\alpha\idtty_n\) para algum \(\alpha\in\bR\), i.e. que \(x_{11}=\dotsb=x_{nn}=\alpha\). Suponhamos a fim de contradição que existam inteiros \(i\) e \(j\) tais que \(1\leq i < j\leq n\) e \(x_{ii}\neq x_{jj}\). Conjugando \(\mathsf X\) por uma matriz de transposição apropriada (ortogonal), podemos também supor, sem perda de generalidade, que \(i=1\) e \(j=2\). Assim, tomando \(\mathsf B\) a matriz-bloco definida por \(\begin{pmatrix} \begin{matrix} 0 & 1\\ 1 & 0 \end{matrix} & {\mathbb 0}_{2\times (n-2)}\\ {\mathbb 0}_{(n-2)\times 2} & \idtty_{n-2} \end{pmatrix}\), e tomando \(\mathsf D\bydef\diag(x_{33},\dotsc,x_{nn})\), temos que
\begin{align*} \mathsf{BX}&=\begin{pmatrix} \begin{matrix} 0 & x_{22} \\ x_{11} & 0 \end{matrix} & {\mathbb 0}_{2\times (n-2)}\\ {\mathbb 0}_{(n-2)\times 2} & \mathsf D \end{pmatrix}\quad\text{e}\\ \mathsf{XB}&=\begin{pmatrix} \begin{matrix} 0 & x_{11} \\ x_{22} & 0 \end{matrix} & {\mathbb 0}_{2\times (n-2)}\\ {\mathbb 0}_{(n-2)\times 2} & \mathsf D \end{pmatrix}\,, \end{align*}contradizendo que \(R_{\mathsf X}\) é reflexiva.
(Necessidade) Suponhamos que \(\mathsf X=\alpha\idtty_n\) para algum \(\alpha\in\bR\) qualquer. Vamos mostrar que \(R_{\mathsf X}\) é reflexiva. Ora, para todo \(\mathsf A\in\mathscr M_n\),
\begin{align*} \mathsf{AX}&=\mathsf A(\alpha\idtty_n)=\alpha\mathsf A\quad\text e\\ \mathsf{XA}&=(\alpha\idtty_n)\mathsf A=\alpha\mathsf A\,, \end{align*}e, portanto, \(\mathsf {AX}=\mathsf{XA}\), como queríamos. □
AULA 5: Introdução a sequências, recorrências, e algoritmos recursivos
DEFINIÇÃO 5.1. Seja \(A\) um conjunto qualquer. Uma sequência de elementos de \(A\) é uma função \(a\) de algum subconjunto contíguo \(X\) de \(\bN\) em \(A\), sendo a imagem de cada \(i\in X\) por \(a\) chamado de o \(i\)-ésimo termo da sequência e denotado por \(a_i\). Quando \(X\) é infinito, dizemos que a sequência é infinita. Quando \(X\) é finito, dizemos que a sequência é finita e que \(\lvert X\rvert\) é o comprimento da sequência. Quando \(A\) é um conjunto de números, a sequência é dita uma sequência numérica.
Como exemplo, já apresentamos a sequência dos números de Fibonacci na Aula 2, uma sequência numérica infinita. Um outro exemplo interessante é a sequência de Collatz para \(n\), sendo \(n\) qualquer inteiro positivo, definida por:
\begin{align*} a_0 &= n\\ a_{i+1} &= \frac{a_i}2\,,&&\text{se $a_i$ é par, $\forall i\geq 0$;}\\ a_{i+1} &= 3{a_i}+1\,,&&\text{se $a_i$ é ímpar, $\forall i\geq 0$.} \end{align*}Observe que esta é uma sequência infinita. A seguir exibimos os primeiros termos desta sequência para \(1\leq n\leq 7\).
\begin{gather*} 1,4,2,1,4,2,1,\dotsc\\ 2,1,4,2,1,4,2,1\dotsc\\ 3,10,5,16,8,4,2,1,4,2,1,\dotsc\\ 4,2,1,4,2,1,\dotsc\\ 5,16,8,4,2,1,4,2,1,\dotsc\\ 6,3,10,5,16,8,4,2,1,4,2,1,\dotsc\\ 7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1,4,2,1,\dotsc \end{gather*}Note-se que, para os exemplos apresentados, a sequência sempre converge para o ciclo \(4,2,1,4,2,1,\dotsc\). O matemático alemão L. Collatz conjecturou em 1937 que esta convergência ocorre para todo inteiro positivo \(n\). No entanto, a conjectura permanece aberta até hoje.
Sequências como as de Fibonacci e de Collatz são definidas recursivamente, estabelecendo os primeiros termos explicitamente, na base da recursão, e os demais termos através de uma recorrência. Uma recorrência é uma equação em que, para definir um termo de uma sequência no lado esquerdo da equação, recorre-se a outros termos da mesma sequência no lado direito. No caso da sequência de Fibonacci, temos a recorrência
\begin{equation*} F_{n}=F_{n-1}+F_{n-2}\,,\quad\text{para $n\geq 2$,} \end{equation*}assim como no caso das sequências de Collatz temos as recorrências:
\begin{align*} a_{i+1} &= \frac{a_i}2\,,&&\text{se $a_i$ é par, para $i\geq 0$;}\\ a_{i+1} &= 3{a_i}+1\,,&&\text{se $a_i$ é ímpar, para $i\geq 0$.} \end{align*}Uma fórmula contendo recorrências é dita aberta. Em contrapartida, uma fórmula fechada é uma fórmula não recorrente. Por exemplo,
\begin{equation*} F_n = \frac{1}{\sqrt 5}(\upphi^n - \upphihat^n) \end{equation*}é uma fórmula fechada para o \(n\)-ésimo termo da sequência de Fibonacci, como provamos no Teorema 2.9.
Recorrências emergem naturalmente da estrutura de diversos problemas em Combinatória.
EXEMPLO 5.2. Alice envia mensagens secretas cifradas em binário para Bob. Como no código que eles estabeleceram entre eles nunca ocorre um par de \(0\)s consecutivos, Alice utiliza o sufixo \(00\) para marcar o fim da mensagem, situação em que Bob encerra a transmissão imediatamente. Para \(n\geq 2\), seja \(R(n)\) o número de mensagens diferentes de comprimento \(n\) que Alice pode enviar a Bob. Por exemplo, para \(n=4\), temos \(R(n)=2\), pois são \(2\) as possibilidades: \(0100\) e \(1100\). Escreva uma fórmula fechada para \(R(n)\) em função de \(n\).
Resolução. Sendo \(k\) um inteiro não-negativo, seja \(X(k)\) o conjunto das strings binárias de comprimento \(k\) que não terminam em \(0\) e que não contêm \(00\) como substring. Seja \(f(k)=\lvert X(k)\rvert\). Para todo inteiro \(n\geq 2\), uma string binária \(s\) de comprimento \(n\) é uma string que Alice pode enviar a Bob se e somente se \(s\) é da forma \(s=x00\) para algum \(x\in X(n-2)\). Assim, \(R(n)=f(n-2)\).
Vamos agora achar uma fórmula fechada para \(f(k)\) para \(k\in\bN\). Como \(X(1)=\{1\}\) e \(X(0)\) contém unicamente a string vazia, temos que \(f(0)=f(1)=1\). Para \(k\geq 2\), temos que uma string binária \(x\) está em \(X(k)\) se e somente se \(x\) é da forma \(x=1y\), para algum \(y\in X(k-1)\), ou \(x=01z\), para algum \(z\in X(k-2)\). Logo, para \(k\geq 2\), temos a recorrência
\begin{equation} \label{eqrec} f(k)=f(k-1)+f(k-2)\,. \end{equation}Ora, então \(f(k)\) é o \((k+1)\)-ésimo número de Fibonacci. Portanto,
\begin{equation*} f(k) = \frac{1}{\sqrt 5}(\upphi^{k+1} - \upphihat^{k+1})\,, \end{equation*}e, consequentemente,
\begin{equation*} R(n) = \frac{1}{\sqrt 5}(\upphi^{n-1} - \upphihat^{n-1})\,.\quad\scriptstyle\text{□} \end{equation*}EXEMPLO 5.3. Sendo \(n\) um inteiro não-negativo, seja \(S(n)\) o maior número de regiões que é possível obter dispondo \(n\) retas no plano. Por exemplo, \(S(3)=7\), conforme ilustra a figura a seguir.
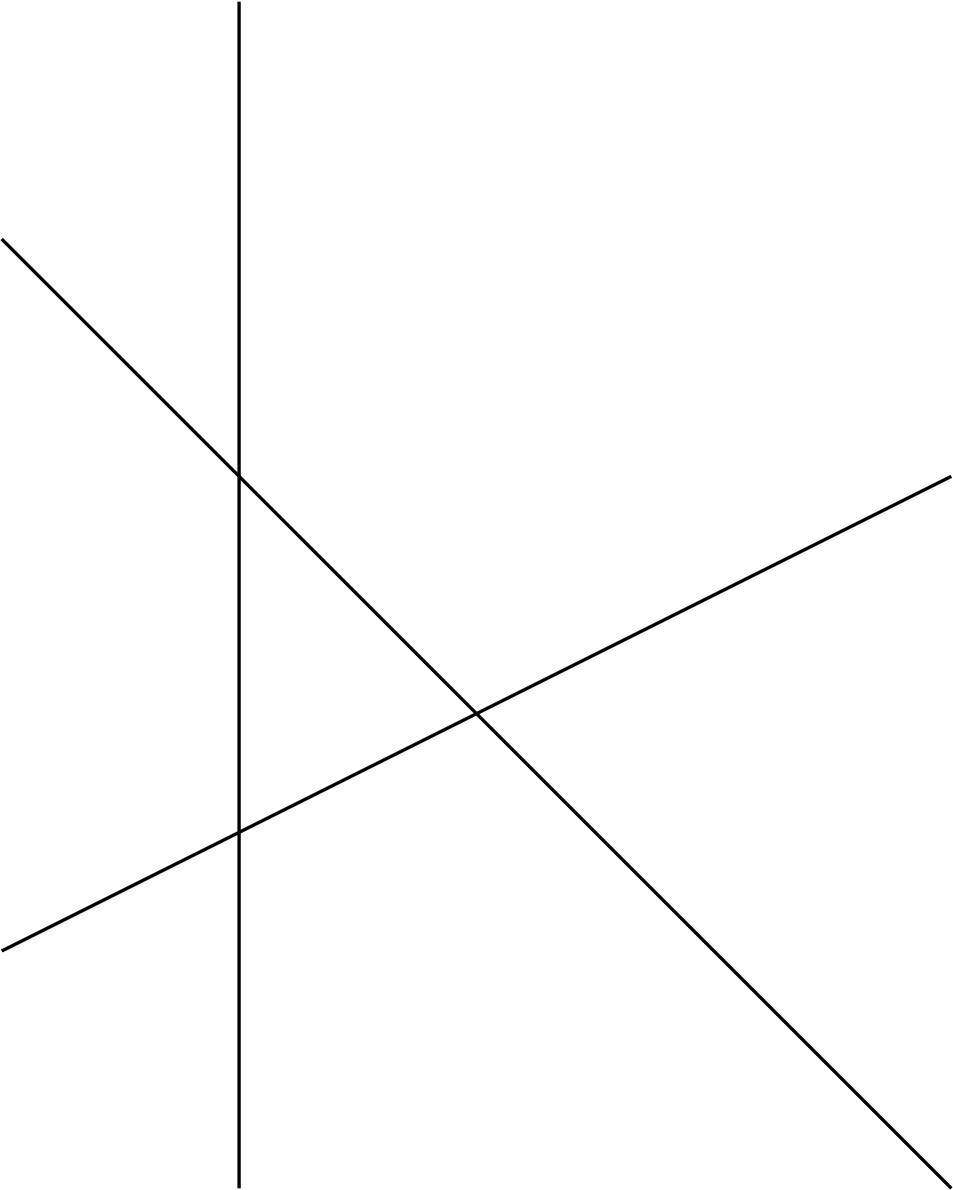
Encontre uma fórmula fechada para \(S(n)\).
Resolução. É imediato que \(S(0)=1\). Para \(n > 0\), temos que, para qualquer conjunto de \(n-1\) retas dispostas sobre o plano, é possível dispor uma nova reta \(r\) sobre o plano de modo a intersectar todas as outras: basta que \(r\) não seja paralela a alguma reta já sobre o plano. Para cada reta \(\ell\) dentra as \(n-1\) retas que já estavam sobre o plano, \(r\) intersecta \(\ell\) num único ponto, dividindo de cada lado de \(\ell\) exatamente uma região em duas. Portanto, observando que é possível que as interseções de \(r\) com as demais retas ocorram em \(n-1\) pontos distintos, um para cada reta, a disposição de \(r\) sobre o plano cria \(n\) novas regiões. Não é possível criar mais regiões, uma vez que \(r\) já está intersectando todas as \(n-1\) retas dispostas anteriormente sobre o plano, em \(n-1\) pontos distintos. Assim, temos:
\begin{align*} S(0) &= 1\,;&&\\ S(n) &= S(n-1) + n\,,&&\text{se $n > 0$.} \end{align*}Vamos agora mostrar que \(S(n)=1+\sum_{i=1}^ni\). Se \(n=0\), a afirmação se verifica, uma vez que \(\sum_{i=1}^0i=0\). Suponhamos, então, que \(n > 0\) e, por indução em \(n\), que, para todo inteiro não-negativo \(n' < n\), valha que \(S(n')=1+\sum_{i=1}^{n'}i\). Como \(n > 0\), temos da recorrência que
\begin{equation*} S(n) = S(n-1) + n\,. \end{equation*}Como, da hipótese da indução, \(S(n-1)= 1+\sum_{i=1}^{n-1}i\), temos
\begin{equation*} S(n) = 1+\sum_{i=1}^{n-1}i + n = 1+\sum_{i=1}^{n}i\,, \end{equation*}como queríamos.
Como, do Teorema 2.2, temos \(\sum_{i=1}^ni=n(n+1)/2\), chegamos à fórmula fechada
\begin{equation*} S(n) = 1 + \frac{n(n+1)}2\,.\quad\scriptstyle\text{□} \end{equation*}EXEMPLO 5.4. No Problema das Torres de Hanoi, temos três torres, \(A\), \(B\), e \(C\), de pratos de diâmetros todos distintos. Inicialmente, temos todos os \(n\geq 1\) pratos sobre a torre \(A\), ordenados da base da torre até o topo em ordem decrescente de diâmetro, estando as demais torres vazias, como ilustra a figura a seguir.
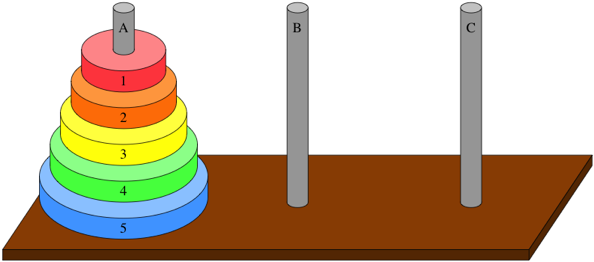
Crédito da imagem: khanacademy.org
Queremos mover todos os pratos da torre \(A\) para a torre \(C\), usando a torre \(B\) como auxiliar. Podemos mover apenas um prato por vez, sempre do topo de uma torre para o topo de outra, e nunca colocando um prato sobre outro de diâmetro menor. Seja \(T(n)\) o número mínimo de movimentos para se moverem os \(n\) pratos de \(A\) para \(C\). Encontre uma fórmula fechada para \(T(n)\).
Resolução. Seja \(T(n,X,Y,Z)\) o número mínimo de movimentos para se moverem \(n\) pratos de \(X\) para \(Z\) usando \(Y\) como auxiliar, sendo \(X,Y,Z\) uma permutação qualquer das três torres \(A,B,C\). Evidentemente, da simetria do problema, \(T(n)=T(n,X,Y,Z)\) para qualquer permutação \(X,Y,Z\). Primeiramente, vamos encontrar uma fórmula aberta para \(T(n,A,B,C)\).
Se \(n=1\), temos \(T(n,A,B,C)=1\), pois basta mover o único prato de \(A\) diretamente para \(C\) para resolvermos o problema em um único movimento. Suponhamos, então, que \(n > 1\). Suponhamos também, sem perda de generalidade, que os diâmetros dos pratos são os inteiros \(1,2,\dotsc,n\), e, para \(1\leq i\leq n\), seja \(p_i\) o prato de diâmetro \(i\). Como o prato \(p_n\) está na base de \(A\), precisamos que todos os pratos \(p_1,\dotsc,p_{n-1}\) estejam em \(B\) no momento em que \(p_n\) for movido de \(A\) para \(C\). Então, se resolvermos o problema de mover os \(n-1\) pratos \(p_1,\dotsc,p_{n-1}\) de \(A\) para \(B\), podemos mover \(p_n\) diretamente para \(C\) e, como \(p_n\) é de diâmetro maior que todos os outros pratos, ficamos com o problema de mover novamente os \(n-1\) pratos \(p_1,\dotsc,p_{n-1}\), mas desta vez de \(B\) para \(C\). Assim, temos a desigualdade
\begin{equation*} T(n,A,B,C) \leq T(n-1, A,C,B) + 1 + T(n-1,B,A,C)\,, \end{equation*}da qual segue
\begin{equation} \label{eqhanoi} T(n) \leq 2T(n-1) + 1\,. \end{equation}Vamos mostrar que o limitante superior para \(T(n)\) em \eqref{eqhanoi} é também um limitante inferior, concluindo que \(T(n)=2T(n-1)+1\). Ora, precisamos mover todos os \(n\) pratos de \(A\) para \(C\), inclusive o prato \(p_n\). Portanto, na solução ótima do problema, sendo \(X,Y,Z\) uma permutação de \(A,B,C\), ao menos uma vez o prato \(p_n\) é movido de uma torre \(X\) para uma torre \(Y\), o que só é possível se todos os demais pratos estiverem na torre \(Z\), tendo chegado lá com pelo menos \(T(n-1)\) movimentos, uma vez que começam todos sobre o prato \(p_n\) em \(A\). Como todos os \(n-1\) pratos \(p_1,\dotsc,p_{n-1}\) começam sobre \(p_n\) terminam sobre \(p_n\) em \(C\), temos que, no último movimento de \(p_n\) para \(C\) na solução ótima, os demais pratos precisam estar em \(B\), e ainda precisam mover-se todos sobre \(p_n\) em \(C\) com pelo menos \(T(n-1)\) movimentos. Logo, temos \(T(n)\geq 2T(n-1)+1\), conforme anunciáramos.
Assim, nossa fórmula aberta para \(T(n)\) é:
\begin{equation*} T(n)=\left\{ \begin{aligned} & 1\,,&&\text{se $n=1$;}\\ & 2T(n-1)+1\,,&&\text{se $n > 1$.} \end{aligned} \right. \end{equation*}Vamos mostrar que
\begin{equation*} T(n)=2^{n}-1\,. \end{equation*}Da fórmula aberta, \(T(1)=1=2^1-1\). Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que para todo inteiro não-negativo \(n' < n\) valha que \(T(n')=2^{n'}-1\). Novamente da fórmula aberta, \(T(n)=2T(n-1)+1\), e, da hipótese da indução, \(T(n-1)=2^{n-1}-1\). Portanto,
\begin{equation*} T(n)=2(2^{n-1}-1)+1=2^{n}-1\,, \end{equation*}como queríamos. □
EXEMPLO 5.5. Considere a seguinte variante do Problema de Josefo, a qual remete a uma lenda envolvendo o grande historiador judeu do sec. I, Flávio Josefo. Na nossa variante, Josefo foi capturado pelos soldados romanos junto com outros judeus, totalizando \(n\) pessoas capturadas. Os demais judeus, preferindo o suicídio a serem mantidos reféns dos romanos, dispuseram-se então num círculo, numerando-se de \(1\) a \(n\), no sentido horário. Então, também no sentido horário, cada segunda pessoa viva se suicidaria, uma por vez. Por exemplo, para \(n=10\), a ordem em que as pessoas se suicidariam seria \(2,4,6,8,10, 3, 7, 1, 9, 5\). Josefo, querendo evitar o suicídio, calculou rapidamente rapidamente em qual posição \(J(n)\) do círculo deveria ficar para ser o último, e então sobreviver. Encontre uma fórmula fechada para \(J(n)\).
Resolução. Vamos inicialmente encontrar uma fórmula aberta para \(J(n)\). É imediato que \(J(1)=1\). Suponhamos, portanto, que \(n > 1\). Temos dois casos.
Se \(n\) é par, as primeiras \(n/2\) pessoas a se suicidarem correspondem exatamente a todos os números pares entre \(1\) e \(n\), inclusive. Após estas pessoas se suicidarem, se renumeramos as pessoas sobreviventes de \(1\) até \(n/2\), ficamos com a instância do mesmo problema para \(n/2\) pessoas. Sendo \(i\) a solução do problema para a instância com \(n/2\) pessoas, esta posição corresponde à posição \(2i-1\) na instância original do problema. Logo, neste caso, temos a recorrência
\begin{equation*} J(n) = 2J\Bigl(\frac n2\Bigr) - 1\,. \end{equation*}Se \(n\) é ímpar, as primeiras \((n-1)/2\) pessoas a se suicidarem correspondem exatamente a todos os números pares entre \(1\) e \(n\), e pessoa seguinte a cometer suicídio é a pessoa de número \(1\). Após todas estas \((n+1)/2\) pessoas se suicidarem, se renumeramos as pessoas sobreviventes de \(1\) até \((n-1)/2\), ficamos com a instância do mesmo problema para \((n-1)/2\) pessoas. Sendo \(i\) a solução do problema para a instância com \((n-1)/2\) pessoas, esta posição corresponde à posição \(2i+1\) na instância original do problema. Logo, neste caso, temos a recorrência
\begin{equation*} J(n) = 2J\Bigl(\frac {n-1}2\Bigr) + 1\,. \end{equation*}
Assim, nossa fórmula aberta é:
\begin{equation*} J(n) = \left\{ \begin{aligned} & 1\,,&&\text{se $n=1$;}\\ & 2J\Bigl(\frac n2\Bigr) - 1\,,&&\text{se $n$ é par;}\\ & 2J\Bigl(\frac {n-1}2\Bigr) + 1\,,&&\text{se $n > 1$ é ímpar.} \end{aligned} \right. \end{equation*}Seja \(2^m\), para \(m\geq 0\), a maior potência de \(2\) tal que \(2^m\leq n\), e seja \(r\in\bN\) tal que \(n=2^m+r\). Vamos provar que
\begin{equation*} J(n) = 2r + 1\,. \end{equation*}Ora, para \(n=1=2^0+0\), temos de fato \(J(1)=2\cdot 0 + 1=1\). Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que, para todo inteiro positivo \(n' < n\), valha que \(J(2^{m'}+r') = 2r' + 1\), sendo \(2^{m'}\) a maior potência de \(2\) tal que \(2^{m'}\leq n'\) e \(r'\in\bN\) tal que \(n'=2^{m'}+r'\). Temos dois casos.
Se \(n\) é par, então, da fórmula aberta,
\begin{align*} J(n) &= 2J\Bigl(\frac{2^{m} + r}2\Bigr) -1\\&= 2J\Bigl(2^{m-1} + \frac{r}2\Bigr) -1\,. \end{align*}Como \(2^m\) é a maior potência de \(2\) tal que \(2^m\leq n\), temos que \(2^{m-1}\) é a maior potência de \(2\) tal que \(2^{m-1}\leq n/2\). Logo, temos da hipótese da indução que \(J(2^{m-1}+r/2)=r+1\), e, portanto,
\begin{equation*} J(n) = 2(r+1) -1 = 2r + 1\,, \end{equation*}como queríamos.
Se \(n\) é ímpar, então, da fórmula aberta,
\begin{align*} J(n) &= 2J\Bigl(\frac{2^{m} + r-1}2\Bigr) +1\\&= 2J\Bigl(2^{m-1} + \frac{r-1}2\Bigr) +1\,. \end{align*}Como \(2^m\) é a maior potência de \(2\) tal que \(2^m\leq n\), temos que \(2^{m-1}\) é a maior potência de \(2\) tal que \(2^{m-1}\leq (n-1)/2\). Logo, temos da hipótese da indução que \(J(2^{m-1}+(r-1)/2)=r\), e, portanto,
\begin{equation*} J(n) = 2r +1 \,, \end{equation*}como queríamos. □
Assim como sequências podem ser definidas recursivamente, podemos utilizar recursão para definir conjuntos.
EXEMPLO 5.6. Seja \(X\) o conjunto de inteiros definido recursivamente por:
Mostre que \(X=3{\mathbb Z}_{> 0}\).
Resolução. Vamos mostrar primeiro que \(3{\mathbb Z}_{> 0}\subseteq X\). Para tanto, sendo \(n\in{\mathbb Z}_{> 0}\), vamos mostrar que \(3n\in X\). Se \(n=1\), temos de 1 que \(3n=3\in X\). Suponhamos, então, que \(n > 1\) e, por indução em \(n\), que, para todo inteiro \(n'\) tal que \(1\leq n' < n\), temos \(3n'\in X\). Ora, \(3n = 3 + 3(n-1)\) e, como \(n > 1\), temos tanto que \(3\in X\), da base da indução, quanto que \(3(n-1)\in X\), da hipótese da indução. Assim, de (2), \(3+3(n-1)=3n\in X\), como queríamos.
Vamos agora mostrar que \(X\subseteq 3{\mathbb Z}_{> 0}\). Para tanto, por indução estrutural na definição de \(X\), basta mostrarmos que:
(a) \(3\in 3{\mathbb Z}_{> 0}\);
(b) para quaisquer \(n_1,n_2\in X\cap 3{\mathbb Z}_{> 0}\), temos \(n_1+n_2\in 3{\mathbb Z}_{> 0}\).
Ora, (a) é trivial. Para mostrarmos (b), sejam \(n_1,n_2\in X\cap 3{\mathbb Z}_{> 0}\). Assim, existem \(t_1,t_2\in{\mathbb Z}_{> 0}\) tais que \(n_1=3t_1\) e \(n_2=3t_2\). Logo, \(n_1+n_2=3(t_1+t_2)\in 3{\mathbb Z}_{> 0}\), como queríamos. □
Fórmulas recursivas também podem nos trazer algoritmos. Por exemplo, para inteiros não-negativos \(a\) e \(b\) não ambos iguais a zero, a fórmula aberta para o maior divisor comum entre \(a\) e \(b\)
\begin{equation*} \gcd(a,b)=\left\{ \begin{aligned} &a&&\text{se $b=0$,}\\ &\gcd(b, a \bmod b)&&\text{se $b > 0$,}\\ \end{aligned} \right. \end{equation*}nos traz imediatamente o clássico Algoritmo de Euclides.
\(\underline{\text{Euclides}(a,b)}\):
- se \(b=0\), devolva \(a\);
- devolva \(\text{Euclides}(b, a \bmod b)\).
TEOREMA 5.7. Sendo \(a\) e \(b\) inteiros não-negativos não sendo ambos iguais a zero, \({\text{Euclides}(a,b)}=\gcd(a,b)\).
Demonstração. Se \(b=0\), então \(a > 0\), e temos \({\text{Euclides}(a,b)}=a\) e \(\gcd(a,b)=a\), pois todo número é divisor de \(0\) (o que implica que o maior divisor de \(a > 0\) que também é divisor de \(0\) é o próprio \(a\)). Suponhamos, então, que \(b > 0\) e, por indução em \(b\), que para todo par de inteiros não-negativos \((a',b')\), não ambos iguais a zero, satisfazendo \(a'\geq b'\) e \(b' < b\), temos que \({\text{Euclides}(a',b')}=\gcd(a',b')\).
Ora, como \(b > 0\), temos, do algoritmo, que \({\text{Euclides}(a,b)}={\text{Euclides}(b, a \bmod b)}\). Observe-se que, independentemente se \(a\geq b\) ou \(a < b\), temos \(b > a\bmod b\). Assim, o par \((b, a \bmod b)\) satisfaz as condições da hipótese da indução, e, portanto, \({\text{Euclides}(b,a\bmod b)}=\gcd(b, a\bmod b)\). Vamos mostrar que \(\gcd(a,b)=\gcd(b,a\bmod b)\).
Seja \(r=a\bmod b\), i.e. \(r\) é o inteiro tal que \(0\leq r < b\) e \(a=bk + r\) para algum \(k\in\bZ\). Assim, para todo divisor \(d\) comum a \(a\) e \(b\), temos \(k_1,k_2\in\bZ\) tais que
\begin{align*} a&=dk_1\quad\text e\\ b&=dk_2\,, \end{align*}o que nos traz que
\begin{align*} r &= a - bk\\ &= dk_1 - dk_2k\\ &= d(k_1-k_2k)\,, \end{align*}e, portanto, que \(d\) divide também \(r\).
Assim, mostramos que o conjunto de todos os divisores comuns entre \(a\) e \(b\) é igual ao conjunto de todos os divisores comuns entre \(a\), \(b\), e \(r\). Para concluirmos a demonstração de que o conjunto dos divisores comuns entre \(a\) e \(b\) é igual ao conjunto dos divisores comuns entre \(b\) e \(r\), do que segue \(\gcd(a,b)=\gcd(b,r)\), precisamos ainda mostrar que \(b\) e \(r\) não têm divisor comum algum que não seja também divisor de \(a\). Ora, para todo divisor \(c\) comum a \(b\) e \(r\), existem \(q_1,q_2\in\bZ\) tais que
\begin{align*} b&= cq_1\\ r&= cq_2\,. \end{align*}Consequentemente,
\begin{equation*} a = bk + r= cq_1k+cq_2=c(q_1k+q_2)\,, \end{equation*}e, portanto, \(c\) também é um divisor de \(a\), como queríamos. □
TEOREMA 5.8. Sejam \(a\) e \(b\) inteiros não-negativos não ambos iguais a zero tais que \(a\geq b\), e seja \(n\) o número de chamadas recursivas feitas por \({\text{Euclides}(a,b)}\) para calcular \(\gcd(a,b)\). Então, \(a\geq F_{n}\) e \(b\geq F_{n-1}\).
Demonstração. Se só uma chamada é realizada por por \({\text{Euclides}(a,b)}\) para calcular \(\gcd(a,b)\), é porque \(b=0\), o que implica \(a > 0\), e de fato temos \(b\geq F_{1-1}=0\) e \(a\geq F_1=1\). Suponhamos, então, que \(a\geq b > 0\) e, por indução em \(b\), que para quaisquer \(x\) e \(y\) inteiros não-negativos não ambos iguais a zero tais que \(x\geq y\) e \(y < b\), valha que \(x\geq F_{E(x,y)}\) e \(y\geq F_{E(x,y)-1}\), sendo \(E(x,y)\) o número de chamadas recursivas que \({\text{Euclides}(x,y)}\) realiza para calcular \(\gcd(x,y)\).
Como \(b > 0\), sabemos que
\begin{equation} \label{euclfib} n=E(a,b)=1+E(b, a\bmod b)\,. \end{equation}Como \(a\bmod b < b\), temos, da hipótese da indução, que
\begin{align*} b&\geq F_{n - 1}\\ \text e\qquad a\bmod b&\geq F_{n-2}\,, \end{align*}já que \(E(b, a\bmod b)=n-1\) por \eqref{euclfib}. Ora, \(a=\lfloor a/b\rfloor b+ (a\bmod b)\) e, como \(\lfloor a/b\rfloor\geq 1\) já que \(a\geq b\), temos, portanto, que
\begin{align*} a&=\Bigl\lfloor \frac ab\Bigr\rfloor b+ (a\bmod b)\\ &\geq1\cdot F_{n-1}+F_{n-2}\\ &\geq F_n\,, \end{align*}como queríamos. □
Consideremos agora o seguinte algoritmo, o qual, recebendo um número real \(a\) qualquer e um inteiro não-negativo \(n\), calcula \(a^n\) através do método conhecido como exponenciação binária, ou exponenciação por elevação ao quadrado (em inglês, exponentiation by squaring), ou até exponenciação por elevação ao quadrado iterada (em inglês, exponentiation by repeated squaring).
\(\underline{\text{ExpBin}(a,n)}\):
- se \(n=0\), devolva \(1\);
- se \(n\) é ímpar, devolva \(a\cdot \text{ExpBin}(a,n-1)\);
- \(b\leftarrow \text{ExpBin}(a,n/2)\);
- devolva \(b\cdot b\).
TEOREMA 5.9. Para quaisquer \(a\in\def\bR{\mathbb R}\bR\) e \(n\in\bN\), o algoritmo \({\text{ExpBin}}(a,n)\) devolve \(a^n\) e, se \(n > 0\), realiza a tarefa executando no máximo \(2\lfloor\lg n\rfloor+1\) multiplicações.
Demonstração. Para \(n\in\bN\), seja \(T(n)\) o número de multiplicações realizadas na execução de \({\text{ExpBin}}(a,n)\) para qualquer \(a\in\bR\), uma vez que, do algoritmo, observa-se que tal número de multiplicações depende só de \(n\), não de \(a\).
Se \(n=0\), temos, do algoritmo, que \(\text{ExpBin}(a,n)=1=a^0\), como queríamos. Se \(n=1\), temos
\begin{align*} \text{ExpBin}(a,n)&=a\cdot \text{ExpBin}(a,n-1)=a\cdot 1=a\\ \text e\qquad T(1)=1 \leq 2\lfloor\lg 1\rfloor+1=1\,, \end{align*}também como queríamos. Suponhamos, então, que \(n\geq 2\) e, por indução em \(n\), que, para todo inteiro não-negativo \(k\) com \(1\leq k < n\), valha que \({\text{ExpBin}}(a,k)=a^{k}\) e que \(T(k) \leq 2\lfloor\lg k\rfloor +1\). Temos dois casos:
\(n\) é par
Neste caso, do algoritmo, é feita a chamada recursiva \(\text{ExpBin}(a,n/2)\), e, uma vez que essa chamada se encerre, o resultado é elevado ao quadrado com mais uma multiplicação. Assim,
\begin{align*} \text{ExpBin}(a,n)&=\bigl(\text{ExpBin}(a,n/2)\bigr)^2\quad\text e\\ T(n) &= T(n/2) + 1\,. \end{align*}Pela hipótese da indução,
\begin{equation*} \text{ExpBin}(a,n)=\bigl(a^{\frac n2}\bigr)^2=a^n \end{equation*}e
\begin{align*} T(n) &\leq 2(\lfloor\lg n/2\rfloor +1)\\ &=2\lfloor\lg n - 1\rfloor + 2\\ &= 2\lfloor\lg n \rfloor-2+2\,; \end{align*}portanto,
\begin{equation} \label{eqtexpbin} T(n) \leq 2\lfloor\lg n\rfloor\leq 2\lfloor\lg n\rfloor + 1\,, \end{equation}como queríamos.
\(n\) é ímpar
Neste caso, do algoritmo, é feita a chamada recursiva \(\text{ExpBin}(a,n-1)\), e, uma vez que essa chamada se encerre, o resultado é multiplicado por \(a\). Assim,
\begin{align*} \text{ExpBin}(a,n)&=a\cdot\text{ExpBin}(a,n-1)\quad\text e\\ T(n) &= T(n-1) + 1\,. \end{align*}Como \(n-1\) é par, caímos no caso anterior, do qual temos \({\text{ExpBin}}(a,n-1)=a^{n-1}\) e, por \eqref{eqtexpbin}, \(T(n-1) \leq 2\lfloor\lg (n-1)\rfloor\). Assim,
\begin{align*} \text{ExpBin}(a,n)&=a\cdot a^{n-1}=a^n\quad\text e\\ T(n) &\leq 2\lfloor\lg (n-1)\rfloor+1\\ &\leq 2\lfloor\lg n\rfloor+1\,,\\ \end{align*}como queríamos. □
Note-se que o método de exponenciação binária pode ser adaptado também para outros contextos, como para calcular \({\mathsf A}^n\), sendo \(\mathsf A\) uma matriz quadrada \(k\times k\) sobre \(\mathbb C\), \(n\) um inteiro não-negativo, e \(k\) um inteiro positivo.
\(\underline{\text{ExpBin}(\mathsf A,n)}\):
- se \(n=0\), devolva \({\mathbb 1}_k\);
- se \(n\) é ímpar, devolva \(\mathsf A\cdot \text{ExpBin}(\mathsf A,n-1)\);
- \(\mathsf B\leftarrow \text{ExpBin}(\mathsf A,n/2)\);
- devolva \(B\cdot B\).
De modo análogo a como fizemos no Teorema 5.9, é possível mostrar que \(\text{ExpBin}(\mathsf A,n)\) realiza no máximo \(2\lfloor\lg n\rfloor+1\) multiplicações de matrizes \(k\times k\).
Pré-lista de exercícios
- Uma sequência numérica \(a_0,a_1,a_2,\dotsc\) é dita uma progressão
aritmética se, para \(i\geq 2\), vale que \(a_i-a_{i-1} =
a_{i-1}-a_{i-2}\), sendo o valor desta
subtração denominada a razão, ou diferença comum, da progressão.
Uma sequência numérica \(a_0,a_1,a_2,\dotsc\) é
dita uma progressão geométrica se, para \(i\geq 2\),
vale que \(a_i/a_{i-1} = a_{i-1}/a_{i-2}\), sendo o valor desta
divisão denominada a razão da progressão.
- Sendo \(a_0,a_1,a_2,\dotsc\) uma progressão aritmética de razão \(d\), escreva \(a_n\), para \(n \geq 0\), em função de \(a_0\), \(n\), e \(d\).
- Sendo \(a_0,a_1,a_2,\dotsc\) uma progressão geométrica de razão \(r\), escreva \(a_n\), para \(n \geq 0\), em função de \(a_0\), \(n\), e \(r\).
- Na variante clássica do Problema de Josefo, eram \(n=41\) judeus capturados ao todo, cada terceira (não segunda) pessoa viva se suicidaria, e Josefo queria encontrar as posições em que ele e mais um amigo seu deveriam ficar para serem os dois últimos vivos do grupo. Quais são essas posições? Pesquise sobre a fórmula para essas posições para o caso de \(n\) geral.
- Seja \(J(n)\) a solução para \(n\) para a variante do Problema de Josefo apresentada em aula. Mostre que \(J(n)\) é o número obtido operando-se um deslocamento circular à esquerda na codificação de \(n\) em binário.
- Resolva o Problema 3348 do Beecrowd.
Escreva um programa em C que, ao ler um inteiro positivo \(n\), imprime a sequência de movimentos ótima para o Problema das Torres de Hanoi com \(n\) pratos, conforme o exemplo de saída a seguir para \(n=3\).
A -> C A -> B C -> B A -> C B -> A B -> C A -> C
Considere o seguinte conjunto de palavras \(H\) definido recursivamente por:
- as palavras macaco, mato, moeda, e moto pertencem a \(H\);
- para quaisquer palavras \(x,y\in H\), temos que:
- (\(x\)) é uma palavra de \(H\);
- !\(x\) é uma palavra de \(H\);
- \(x\)+\(y\) é uma palavra de \(H\);
- \(x\)!\(y\) é uma palavra de \(H\).
Mostre que a palavra (mato+macaco)+(moto+moeda) pertence a \(H\), mas a palavra ((macaco)+(mato))!(+moeda+mato) não pertence.
Para \(n\) um inteiro positivo e \(\boldsymbol A[1..n]\) um array de \(n\) inteiros, indexados de \(1\) a \(n\), considere o seguinte algoritmo.
\(\underline{\text{Max}(\boldsymbol A[1..n])}\):
- se \(n=1\), devolva \(\boldsymbol A[1]\);
- \(m\leftarrow \text{Max}(\boldsymbol A[1..(n-1)])\);
- se \(m \leq \boldsymbol A[n]\), devolva \(\boldsymbol A[n]\);
- devolva \(m\).
Mostre que \(\text{Max}(\boldsymbol A[1..n])\) retorna o maior valor do conjunto \(A=\{\boldsymbol A[1],...,\boldsymbol A[n]\}\), realizando \(O(n)\) comparações entre os elementos do conjunto \(A\).
- Leia [CLRS09] Cap. 9 sobre o Problema da Seleção.
A Sequência de Golomb \(G(1),G(2),G(3),\dotsc\) é definida como a única sequência não-decrescente de inteiros positivos que se autodescreve, no sentido de que contém exatamente \(G(k)\) ocorrências do número \(k\) para todo inteiro positivo \(k\). A tabela a seguir exibe os primeiros elementos desta sequência.
\(\boldsymbol k\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) \(7\) \(8\) \(9\) \(10\) \(11\) \(12\) \(\boldsymbol{G(k)}\) \(1\) \(2\) \(2\) \(3\) \(3\) \(4\) \(4\) \(4\) \(5\) \(5\) \(5\) \(6\) Explique a seguinte fórmula para \(G(k)\):
\begin{equation*} G(k) = \left\{ \begin{aligned} & 1\,,&&\text{se $k=1$;}\\ & 1 + G(k-G(G(k-1)))\,,&&\text{se $k > 1$.} \end{aligned} \right. \end{equation*}- Inspirado na fórmula acima, escreva um programa que, recebendo um inteiro \(k\), calcula \(G(k)\). Seu programa é suficientemente eficiente para conseguir passar o Problema UVA 10049? Por quê?
Escreva um programa suficientemente eficiente para conseguir passar o Problema UVA 10049. Dica para conseguir passar o problema: sendo \(f(n)\) a função que define o \(n\)-ésimo número que satisfaz \(G(k) > G(k-1)\) para algum \(k\), complete a recorrência:
\begin{equation*} f(n) = f(n-1)+G(\mathbf{\text{___}})\,. \end{equation*}
- Sendo \(a\), \(b\), e \(n\) inteiros tais que \(0\leq a,b < n\), dizemos que \(b\)
é inverso multiplicativo de \(a\) módulo \(n\) se \(ab\equiv 1\pmod
n\).
- Mostre que \(a\) possui inverso multiplicativo módulo \(n\), e que este inverso é único, se e somente se \(\gcd(a,n)=1\).
- Exiba um algoritmo que, dados \(a\) e \(n\) satisfazendo \(\gcd(a,n)=1\), utiliza o Algoritmo de Euclides Estendido (cf. Exercício 34) para calcular o inverso multiplicativo de \(a\) módulo \(n\).
- Resolva o Problema Beecrowd 1716.
Para \(n\in\bZ_{\geq 0}\), mostre, por indução em \(n\), que, para todo tabuleiro de xadrez \(2^n\times 2^n\) com uma de suas casas ocupadas, é possível cobrir todas as casas livres do tabuleiro com triominós. Exiba também um algoritmo recursivo que, dados um inteiro não-negativo \(n\) e um tabuleiro de xadrez \(2^n\times 2^n\) com uma de suas casas ocupadas, mostra como cobrir todas as casas livres com triominós. A figura a seguir mostra um triominó, um tabuleiro de xadrez \(2^2\times 2^2\) com uma das casas ocupadas, e o mesmo tabuleiro com um triominó cobrindo três de suas casas livres.

AULA 6: Recorrências lineares
DEFINIÇÃO 6.1. Sejam \(f\colon \bN \to\def\bC{\mathbb C}\bC\) e \(k\in\bZ_{> 0}\). Uma recorrência linear homogênea de ordem \(k\) com coeficientes constantes para \(f(n)\) é uma equação da forma
\begin{equation} \label{eqreck} f(n) = a_1f(n-1)+a_2f(n-2)+\dotsb+a_kf(n-k)\quad\text{para $n\geq k$,} \end{equation}sendo \(a_1,a_2,\dotsc,a_k\in\bC\) e \(a_k\neq 0\).
TEOREMA 6.2 Sejam \(k\in\bZ_{> 0}\) e \(a_1,a_2,\dotsc,a_k\in\bC\) com \(a_k\neq 0\). O conjunto \(\mathcal F\) de todas as funções \(f\) de \(\bN\) em \(\bC\) que satisfazem \eqref{eqreck} forma um espaço vetorial com as operações usuais de soma de funções e de multiplicação de função por escalar complexo.
Demonstração. Vamos mostrar que \(\mathcal F\), com as operaçoẽs usuais de soma de funções e multiplicação de função por escalar complexo, satisfaz todos os axiomas da definição de espaço vetorial.
(Associatividade da soma) Sejam \(f,g,h\in\mathcal F\). Para cada \(n < k\), temos \((f(n)+g(n))+h(n)=f(n)+(g(n)+h(n))\) imediatamente da associatividade da soma do corpo dos números complexos. Para \(n\geq k\), temos
\begin{align*} (f(n)+g(n))+h(n) &=\biggl(\sum_{i=1}^ka_if(n-i)+\sum_{i=1}^ka_ig(n-i) \biggl) + \sum_{i=1}^ka_ih(n-i)\\ &=\sum_{i=1}^ka_if(n-i)+\biggl(\sum_{i=1}^ka_ig(n-i) + \sum_{i=1}^ka_ih(n-i) \biggl)\\ &=f(n)+(g(n)+h(n))\,, \end{align*}também como queríamos.
(Comutatividade da soma) Sejam \(f,g\in\mathcal F\). Para cada \(n < k\), temos \(f(n)+g(n)=g(n)+f(n)\) imediatamente da comutatividade da soma do corpo dos números complexos. Para \(n\geq k\), temos
\begin{align*} f(n)+g(n) &=\sum_{i=1}^ka_if(n-i)+\sum_{i=1}^ka_ig(n-i)\\ &=\sum_{i=1}^ka_ig(n-i)+\sum_{i=1}^ka_if(n-i)\\ &=g(n)+f(n)\,, \end{align*}também como queríamos.
(Existência de elemento neutro da soma) Seja \(\boldsymbol 0\) a função definida por \(\boldsymbol 0(n)\bydef 0\) para todo \(n\in\bN\). Observe-se que, para \(n\geq k\),
\begin{equation*} \boldsymbol 0(n)=\sum_{i=1}^ka_i\cdot 0=\sum_{i=1}^ka_i\boldsymbol 0(n-i) \end{equation*}para quaisquer \(a_1,\dotsc,a_k\in\bC\). Portanto, \(\boldsymbol 0\in\mathcal F\). Ademais, para todo \(f\in\mathcal F\), temos
\begin{equation*} f(n)+\boldsymbol 0(n)=f(n)+0=f(n)\,,\quad\forall n\in\bN. \end{equation*}Logo, \(\boldsymbol 0\) é elemento neutro para a soma de funções em \(\mathcal F\).
(Existência de inverso para a soma) Para todo \(f\in\mathcal F\), seja \(-f\) a função definida por \((-f)(n)\bydef-f(n)\) para todo \(n\in\bN\). Observe-se que, para \(n\geq k\), sendo \(a_1,\dotsc,a_k\) tais que \(f(n)=\sum_{i=1}^ka_if(n-i)\), temos
\begin{equation*} (-f)(n)=-\sum_{i=1}^ka_if(n-i)=\sum_{i=1}^k-a_if(n-i) =\sum_{i=1}^ka_i(-f)(n-i) \end{equation*}e, portanto, \(\boldsymbol -f\in\mathcal F\). Ademais, temos, para todo \(n\in\bN\),
\begin{equation*} f(n)+(-f)(n)=f(n)-f(n)=0=\boldsymbol 0(n)\,. \end{equation*}Logo, \(-f\) é o inverso de \(f\) para a soma de funções em \(\mathcal F\).
(Compatibilidade da multiplicação por escalar complexo com a associatividade da multiplicação do corpo) Sejam \(\alpha,\beta\in\bC\) e \(f\in\mathcal F\). Para todo \(n < k\), temos \(\alpha(\beta f(n))=(\alpha\beta)f(n)\) imediatamente da associatividade da multiplicação do corpo dos complexos. Para \(n\geq k\), temos
\begin{align*} \alpha(\beta f(n)) &= \alpha\biggl(\beta\sum_{i=1}^ka_if(n-i)\biggr)\\ &=(\alpha\beta)\sum_{i=1}^ka_if(n-i)\,, \end{align*}também como queríamos.
(Compatibilidade da multiplicação por escalar complexo com o elemento neutro da multiplicação do corpo) Sendo \(f\in\mathcal F\), temos
\begin{equation*} 1\cdot f(n)=f(n)\quad \forall n\in\bN\,, \end{equation*}como queríamos.
(Distributividade da multiplicação por escalar sobre a soma de vetores do espaço) Sejam \(\alpha\in\bC\) e \(f,g\in\mathcal F\). Para todo \(n < k\), temos \(\alpha(f(n)+g(n))=\alpha f(n)+\alpha g(n)\) imediatamente da distributividade da multiplicação sobre a soma no corpo dos números complexos. Para \(n\geq k\), temos
\begin{align*} \alpha(f(n)+g(n))&=\alpha\biggl(\sum_{i=1}^ka_if(n-i)+\sum_{i=1}^ka_ig(n-i)\biggr)\\ &=\alpha\sum_{i=1}^ka_if(n-i)+\alpha\sum_{i=1}^ka_ig(n-i)\\ &=\alpha f(n)+\alpha g(n)\,, \end{align*}também como queríamos.
(Distributividade da multiplicação por escalar sobre a soma de escalares) Sejam \(\alpha,\beta\in\bC\) e \(f\in\mathcal F\). Para todo \(n < k\), temos \((\alpha+\beta)f(n)=\alpha f(n)+\beta f(n)\) imediatamente da distributividade da multiplicação sobre a soma no corpo dos números complexos. Para \(n\geq k\), temos
\begin{align*} (\alpha+\beta)f(n)&=(\alpha+\beta)\sum_{i=1}^ka_if(n-i)\\ &=\alpha\sum_{i=1}^ka_if(n-i)+\beta\sum_{i=1}^ka_if(n-i)\\ &=\alpha f(n)+\beta f(n)\,, \end{align*}também como queríamos. □
TEOREMA 6.3. Sejam \(k\in\bZ_{> 0}\), \(a_1,a_2,\dotsc,a_k\in\bC\) com \(a_k\neq 0\), e \(\mathcal F\) o espaço vetorial das funções \(f\colon \bN\to\bC\) que satisfazem \eqref{eqreck}. Sejam também, do Teorema Fundamental da Álgebra, \(x_1,x_2,\dotsc,x_k\) as \(k\) raízes complexas, não necessariamente distintas, da equação característica
\begin{equation} \label{eqcark} x^k-a_1x^{k-1}-a_2x^{k-2}\dotsb-a_k=0\,. \end{equation}Então:
- para cada \(i\in\{1,\dotsc,k\}\), a função \(x_i^n\) pertence a \(\mathcal F\);
se as \(k\) raízes \(x_1,x_2,\dotsc,x_k\) são todas distintas, então, para todo \(f\in\mathcal F\), sendo \(\lambda_1,\lambda_2,\dotsc,\lambda_k\in\bC\) tais que
\begin{equation*} f(n)=\lambda_1x_1^n+\lambda_2x_2^n+\dotsb+\lambda_kx_k^n\quad\text{para $0\leq n < k$,} \end{equation*}temos
\begin{equation*} f(n)=\lambda_1x_1^n+\lambda_2x_2^n+\dotsb+\lambda_kx_k^n\quad\text{para todo $n\in\bN$.} \end{equation*}
Demonstração. Seja \(x_i\) uma raiz de \eqref{eqcark}. Assim, para todo \(n\geq k\), temos
\begin{equation*} x_i^{n-k}(x_i^k-a_1x_i^{k-1}-a_2x_i^{k-2}\dotsb-a_k)=x_i^{n-k}\cdot0=0\,, \end{equation*}e, portanto,
\begin{equation*} x_i^n=a_1x_i^{n-1}+a_2x_i^{n-2}+\dotsb+a_kx_i^{n-k}\,. \end{equation*}Logo, a função \(x_i^n\) pertence a \(\mathcal F\).
Seja agora \(f\colon \bN\to \bC\) uma função qualquer em \(\mathcal F\). Vamos mostrar que, se as raízes \(x_1,\dotsc,x_k\) são todas distintas, o que implica que o sistema de equações lineares
\begin{equation} \label{sysrec} \left\{\begin{array}{rl} \lambda_1x_1^0+\lambda_2x_2^0+\dotsb+\lambda_kx_k^0&=f(0)\\ \lambda_1x_1^1+\lambda_2x_2^1+\dotsb+\lambda_kx_k^1&=f(1)\\ &\vdots\\ \lambda_1x_1^{k-1}+\lambda_2x_2^{k-1}+\dotsb+\lambda_kx_k^{k-1}&=f(k-1)\\ \end{array}\right. \end{equation}com incógnitas \(\lambda_1,\lambda_2,\dotsc,\lambda_k\) possui solução em \(\bC^k\), então
\begin{equation*} f(n)=\lambda_1x_1^n+\lambda_2x_2^n+\dotsb+\lambda_kx_k^n\,,\quad\forall n\in\bN\,. \end{equation*}Ora, se \eqref{sysrec} possui uma solução \((\lambda_1,\dotsc,\lambda_k)\in\bC^k\), já temos \(f(n)=\sum_{i=1}^k\lambda_ix_i^{n}\) para \(0\leq n < k\). Suponhamos, então, que \(n\geq k\) e, para todo inteiro não-negativo \(n' < n\), que \(f(n')=\sum_{i=1}^k\lambda_ix_i^{n'}\). Como \(f\in\mathcal F\),
\begin{align*} f(n)&=a_1f(n-1)+a_2f(n-2)+\dotsb+a_kf(n-k)\\ &= a_1\sum_{i=1}^k\lambda_ix_i^{n-1}+ a_2\sum_{i=1}^k\lambda_ix_i^{n-2}+\dotsb+ a_k\sum_{i=1}^k\lambda_ix_i^{n-k}\\ &=\sum_{i=1}^k(a_1 \lambda_ix_i^{n-1}+ a_2 \lambda_ix_i^{n-2}+\dotsb+ a_k \lambda_ix_i^{n-k})\\ &=\sum_{i=1}^k\lambda_ix_i^{n-k}(a_1 x_i^{k-1}+ a_2 x_i^{k-2}+\dotsb+a_k)\\ &=\sum_{i=1}^k\lambda_ix_i^{n-k}(x_i^k)\\ &=\sum_{i=1}^k\lambda_ix_i^{n}\,, \end{align*}como queríamos. □
EXEMPLO 6.4. Vamos usar os Teoremas 6.2–6.3 para encontrar a fórmula fechada para o \(n\)-ésimo número de Fibonacci que já apresentamos no Teorema 2.9. Sabemos do Teorema 6.2 que todas as funções \(f\colon\bN\to\bC\) que satisfazem a recorrência
\begin{equation*} f(n)=f(n-1)+f(n-2)\quad\text{para $n\geq 2$,} \end{equation*}formam um espaço vetorial \(\mathcal F\) com as operações usuais de soma de funções e multiplicação de função por escalar complexo. Como a equação característica desta recorrência é
\begin{equation} \label{eqcarfib} x^2-x-1=0\,, \end{equation}e como as raízes de \eqref{eqcarfib} são \(\upphi=(1+\sqrt 5)/2\) e \(\upphihat=(1-\sqrt 5)/2\), temos, do Teorema 6.3, que as funções \(\upphi^n\) e \(\upphihat^n\) pertencem a \(\mathcal F\). Ainda, como o sistema
\begin{equation*} \left\{\begin{array}{rl} \lambda_1\upphi^0+\lambda_2\upphihat^0&=f(0)=0\\ \lambda_1\upphi^1+\lambda_2\upphihat^1&=f(1)=1 \end{array}\right. \end{equation*}possui a solução \(\lambda_1=1/\sqrt5,\lambda_2=-1/\sqrt5\), temos também do Teorema 6.3 a fórmula fechada
\begin{equation*} F_n = \frac{1}{\sqrt 5}(\upphi^n - \upphihat^n)\,,\quad\forall n\in\bN\,.\quad\scriptstyle\text{□} \end{equation*}Com exponenciação binária de matrizes, podemos obter algoritmos eficientes para o cálculo de sequências dadas por recorrências lineares homogêneas, como ilustra o Exemplo 6.5.
EXEMPLO 6.5. Exiba um algoritmo que executa \(O(\log n)\) operações aritméticas para calcular o \(n\)-ésimo número de Fibonacci.
Resolução. Sabemos que o conjunto de todas as funções de \(\bN\) em \(\bC\) que satisfazem a recorrência
\begin{equation*} f(n)=f(n-1)+f(n-2)\quad\text{para $n\geq 2$} \end{equation*}forma um espaço vetorial \(\mathcal F\) com as operações usuais de adição de funções e multiplicação de função por escalar. Ainda, é possível obter uma transformação linear \(\mathsf A\) de \(\bC^2\) em \(\bC^2\) tal que, para todo \(n\geq 2\),
\begin{equation*} \mathsf A\begin{pmatrix} f(n-2)\\ f(n-1) \end{pmatrix}= \begin{pmatrix} f(n-1)\\ f(n) \end{pmatrix}\,, \end{equation*}bastando tomar
\begin{equation*} \mathsf A=\begin{pmatrix} 0 & 1\\ 1 & 1 \end{pmatrix}\,. \end{equation*}Assim, indutivamente, temos, para todo \(n\geq 2\), que
\begin{equation} \label{eqfibm} \mathsf A^{n-1}\begin{pmatrix} f(0)\\ f(1) \end{pmatrix}= \begin{pmatrix} f(n-1)\\ f(n) \end{pmatrix}\,. \end{equation}De \eqref{eqfibm} segue o algoritmo abaixo para o cálculo do \(n\)-ésimo número de Fibonacci.
\(\underline{\text{Fibonacci}(n)}\):
Seja \(P(n)\) o número de operações aritméticas que nosso algoritmo realiza em função de \(n\). Se \(n\leq 1\), temos \(P(n)=0\). Se \(n\geq 2\), podemos implementar a linha 2 com exponenciação binária, realizando no máximo \(2\lfloor \lg (n-1)\rfloor +1=O(\log n)\) multiplicações de matrizes na linha 2, cada uma realizando \(O(1)\) operações aritméticas envolvendo apenas inteiros, uma vez que \(\mathsf A\) é uma matriz de tamanho constante em relação a \(n\), e uma vez que \(\mathsf A\) e \((0,1)^{\top}\) são matrizes de inteiros. Como a linha 3 também custa \(O(1)\) operações aritméticas, temos \(P(n)=O(\log n)\), como queríamos. □
A seguir, um exemplo de como o Teorema 6.3. pode ser aplicado, às vezes, até mesmo para recorrências lineares não-homogêneas, através de uma técnica de homogeneização.
EXEMPLO 6.6. Encontre uma fórmula fechada para a função \(f\colon {\mathbb Z}_{\geq 0}\to{\mathbb Z}_{\geq 0}\) definida por
\begin{equation*} f(n) = \left\{ \begin{aligned} &n&&\text{se \(n\leq 1\),}\\ &f(n-1)+f(n-2)+1&&\text{se \(n\geq 2\).}\\ \end{aligned} \right. \end{equation*}Resolução. Como, para \(n\geq 2\),
\begin{align*} f(n) &= f(n-1)+f(n-2)+1\qquad\text e\\ f(n+1) &= f(n)+f(n-1)+1\,, \end{align*}temos
\begin{equation*} f(n+1)-f(n) = f(n) - f(n-2) \end{equation*}e, portanto,
\begin{equation*} f(n+1) = 2f(n) - f(n-2)\qquad\text{(para \(n+1\geq 3\))}\,. \end{equation*}Assim,
\begin{equation*} f(n) = \left\{ \begin{aligned} &n&&\text{se \(n\leq 2\),}\\ &2f(n-1)-f(n-3)&&\text{se \(n\geq 3\).}\\ \end{aligned} \right. \end{equation*}Sabemos do Teorema 6.2 que todas as funções \(f\colon\bN\to\bC\) que satisfazem a recorrência
\begin{equation*} f(n)=2f(n-1)-f(n-3)\quad\text{para $n\geq 3$,} \end{equation*}formam um espaço vetorial \(\mathcal F\) com as operações usuais de soma de funções e multiplicação de função por escalar complexo. Como a equação característica desta recorrência é
\begin{equation} \label{eqcarfibb} x^3-2x^2+1=0\,, \end{equation}e como as raízes de \eqref{eqcarfibb} são \(1\), \(\upphi=(1+\sqrt 5)/2\), e \(\upphihat=(1-\sqrt 5)/2\), temos, do Teorema 6.3, que as funções \(1^n\), \(\upphi^n\), e \(\upphihat^n\) pertencem a \(\mathcal F\). Ainda, como o sistema
\begin{equation*} \left\{\begin{array}{rl} \lambda_1\cdot1^0+\lambda_2\upphi^0+\lambda_3\upphihat^0&=f(0)=0\\ \lambda_1\cdot1^1+\lambda_2\upphi^1+\lambda_3\upphihat^1&=f(1)=1\\ \lambda_1\cdot1^2+\lambda_2\upphi^2+\lambda_3\upphihat^2&=f(2)=2 \end{array}\right. \end{equation*}possui a solução \(\lambda_1=-1,\lambda_2=(5+3\sqrt 5)/10,\lambda_3=(5-3\sqrt 5)/10\), temos também do Teorema 6.3 a fórmula fechada
\begin{align*} f(n) &= (-1)1^n + \Bigl(\frac{5+3\sqrt 5}{10}\Bigr)\upphi^n + \Bigl(\frac{5-3\sqrt 5}{10}\Bigr)\upphihat^n \\ &= \Bigl(\frac{5+3\sqrt 5}{10}\Bigr)\upphi^n + \Bigl(\frac{5-3\sqrt 5}{10}\Bigr)\upphihat^n - 1\,,\quad\forall n\in\bN\,.\quad\scriptstyle\text{□} \end{align*}Truques similares aos aplicados no Exemplo 6.6 podem ser usados para resolver outros problemas relacionados.
EXEMPLO 6.7. Mostre um algoritmo que executa \(O(\log n)\) operações aritméticas para calcular o valor de \(S(n)\bydef F_0+\dotsb+F_n\).
Resolução. Para todo \(n\geq 0\), sabemos que \(F_n = F_{n+2}-F_{n+1}\). Assim,
\begin{align*} F_0 &= F_2 - F_1\,,\\ F_1 &= F_3 - F_2\,,\\ &\vdots\\ F_{n-1} &= F_{n+1} - F_{n}\,,\\ F_n &= F_{n+2} - F_{n+1}\,, \end{align*}e, somando-se todas as equações, obtemos
\begin{equation*} S(n)=F_{n+2} - F_1\,. \end{equation*}Destarte, um algoritmo para, dado \(n\geq 0\), calcular \(S(n)\) em \(O(\log n)\) operações aritméticas consiste em utilizar o algoritmo apresentado no Exemplo 6.5 para calcular \(F_{n+2}\) e então devolver \(F_{n+2}-1\). □
TEOREMA 6.8. Sejam \(k\in\bZ_{> 0}\), \(a_1,a_2,\dotsc,a_k\in\bC\) com \(a_k\neq 0\), e \(\mathcal F\) o espaço vetorial das funções \(f\colon \bN\to\bC\) que satisfazem \eqref{eqreck}. Sejam também, do Teorema Fundamental da Álgebra, \(x_1,x_2,\dotsc,x_k\) as \(k\) raízes complexas, não necessariamente distintas, de \eqref{eqcark}, de modo que raízes iguais apareçam consecutivas nessa ordem. Ainda, para todo \(i\in\{1,\dotsc,k\}\), seja \(g_i(n)\) a função definida por
\begin{equation*} g_i(n)\bydef\left\{ \begin{aligned} & n g_{i-1}(n) &&\text{se $i > 1$ e $x_i=x_{i-1}$,}\\ &1&&\text{caso contrário.} \end{aligned} \right. \end{equation*}Então,
- para cada \(i\in\{1,\dotsc,k\}\), a função \(g_i(n)x_i^n\) pertence a \(\mathcal F\);
para todo \(f\in\mathcal F\), sendo \(\lambda_1,\lambda_2,\dotsc,\lambda_k\in\bC\) tais que
\begin{equation*} f(n)=\lambda_1g_1(n)x_1^n+\lambda_2g_2(n)x_2^n+\dotsb+\lambda_kg_k(n)x_k^n\quad\text{para $0\leq n < k$,} \end{equation*}temos
\begin{equation*} f(n)=\lambda_1g_1(n)x_1^n+\lambda_2g_2(n)x_2^n+\dotsb+\lambda_kg_k(n)x_k^n\quad\text{para todo $n\in\bN$.} \end{equation*}
Demonstração. Sabemos, do Teorema 6.3, que para toda raiz \(r\) de \eqref{eqcark}, a função \(r^n\) pertence a \(\mathcal F\). Para mostrar (1), é suficiente mostrar que se a multiplicidade \(m\) da raiz \(r\) é maior que \(1\), então a função \(n^ir^n\) satisfaz \eqref{eqreck} para todo \(i\in\{1,\dotsc,m-1\}\). Suponhamos, então, que \(m > 1\). Para \(n\in{\mathbb Z}_{\geq k}\), sejam \(p_0,p_1,\dotsc,p_{m-1}\colon\bC\to\bC\) os polinômios dados por por
\begin{align*} p_0(x)&=x^{n}-a_1x^{n-1}-a_2x^{n-2}\dotsb-a_kx^{n-k}\,,&&\text{e}\\ p_i(x)&=x\Bigl(\frac{\mathrm dp_{i-1}(x)}{\mathrm dx}\Bigr)&&\text{para $i > 0$.} \end{align*}Vamos mostrar que, para todo \(i\in\{0,\dotsc,m-1\}\),
\begin{equation*} p_i(x)=n^ix^{n}-a_1(n-1)^ix^{n-1}-a_2(n-2)^ix^{n-2}\dotsb-a_k(n-k)^ix^{n-k} \end{equation*}e que todas as raízes não-nulas de \(p_i(x)=0\) são também raízes de \(p_0(x)=0\), o que implica, já que \(i < m\), que \(r\) é uma raiz de \(p_i(x)=0\) e que \(n^ir^n\) satisfaz \eqref{eqreck}, como queríamos. Se \(i=0\), já sabemos que \(p_0(x)=x^{n}-a_1x^{n-1}-a_2x^{n-2}\dotsb-a_kx^{n-k}\). Suponhamos, então, que \(0 < i \leq m - 1\) e que, para todo inteiro não-negativo \(j < i\), valha que
\begin{equation*} p_j(x)=n^jx^{n}-a_1(n-1)^jx^{n-1}-a_2(n-2)^jx^{n-2}\dotsb-a_k(n-k)^jx^{n-k} \end{equation*}e que todas as raízes não-nulas de \(p_j(x)=0\) são também raízes de \(p_0(x)=0\). Ora, \(p_i(x)=x(\mathrm dp_{i-1}(x)/\mathrm dx)\) e, da hipótese da indução
\begin{equation*} p_{i-1}(x)=n^{i-1}x^{n}-a_1(n-1)^{i-1}x^{n-1}-a_2(n-2)^{i-1}x^{n-2}\dotsb-a_k(n-k)^{i-1}x^{n-k}\,. \end{equation*}Assim,
\begin{align*} p_i(x) &= x\Bigl(\frac{\mathrm dp_{i-1}(x)}{\mathrm dx}\Bigr)\\ &= x\bigl( n^{i-1+1}x^{n-1}-a_1(n-1)^{i-1+1}x^{n-2}-a_2(n-2)^{i-1+1}x^{n-3}\dotsb-a_k(n-k)^{i-1+1}x^{n-k-1}\bigr)\\ &= n^ix^{n}-a_1(n-1)^ix^{n-1}-a_2(n-2)^ix^{n-2}\dotsb-a_k(n-k)^ix^{n-k}\,, \end{align*}como queríamos. Ainda, já que \(p_i(x)=x(\mathrm dp_{i-1}(x)/\mathrm dx)\), temos que todas as raízes não-nulas de \(p_i(x)=0\) são raízes de \(\mathrm dp_{i-1}(x)/\mathrm dx=0\), portanto raízes de \(p_{i-1}(x)=0\), e consequentemente, da hipótese da indução, raízes de \(p_0(x)=0\), também como queríamos.
Seja agora \(f\colon \bN\to \bC\) uma função qualquer em \(\mathcal F\). Observe que o sistema de equações lineares
\begin{equation} \label{sysrec1} \left\{\begin{array}{rl} \lambda_1g_1(0)x_1^0+\lambda_2g_2(0)x_2^0+\dotsb+\lambda_kg_k(0)x_k^0&=f(0)\\ \lambda_1g_1(1)x_1^1+\lambda_2g_2(1)x_2^1+\dotsb+\lambda_kg_k(1)x_k^1&=f(1)\\ &\vdots\\ \lambda_1g_1(k-1)x_1^{k-1}+\lambda_2g_2(k-1)x_2^{k-1}+\dotsb+\lambda_kg_k(k-1)x_k^{k-1}&=f(k-1)\\ \end{array}\right. \end{equation}com incógnitas \(\lambda_1,\lambda_2,\dotsc,\lambda_k\) sempre possui solução em \(\bC^k\). Assim, já temos \(f(n)=\sum_{i=1}^k\lambda_ig_i(n)x_i^{n}\) para \(0\leq n < k\). Suponhamos, então, que \(n\geq k\) e, para todo inteiro não-negativo \(n' < n\), que \(f(n')=\sum_{i=1}^k\lambda_ig_i(n')x_i^{n'}\). Como \(f\in\mathcal F\),
\begin{align*} f(n)&=a_1g_1(n-1)f(n-1)+a_2g_1(n-2)f(n-2)+\dotsb+a_kg_k(n-k)f(n-k)\\ &= a_1\sum_{i=1}^k\lambda_ig_i(n-1)x_i^{n-1}+ a_2\sum_{i=1}^k\lambda_ig_i(n-2)x_i^{n-2}+\dotsb+ a_k\sum_{i=1}^k\lambda_ig_i(n-k)x_i^{n-k}\\ &=\sum_{i=1}^k(a_1 \lambda_ig_i(n-1)x_i^{n-1}+ a_2 \lambda_ig_i(n-2)x_i^{n-2}+\dotsb+ a_k \lambda_ig_i(n-k)x_i^{n-k})\\ &=\sum_{i=1}^k\lambda_i(a_1 g_i(n-1)x_i^{n-1}+ a_2 g_i(n-2)x_i^{n-2}+\dotsb+ a_k g_i(n-k)x_i^{n-k})\\ &=\sum_{i=1}^k\lambda_ig_i(n)x_i^{n}\,, \end{align*}como queríamos. □
EXEMPLO 6.9. Encontre uma fórmula fechada para a função \(f\colon {\mathbb Z}_{\geq 0}\to{\mathbb Z}_{\geq 0}\) definida por
\begin{equation*} f(n) = \left\{ \begin{aligned} &n&&\text{se \(n\leq 3\),}\\ &5f(n-1)-6f(n-2)-4f(n-3)+8f(n-4)&&\text{se \(n\geq 4\).}\\ \end{aligned} \right. \end{equation*}Resolução. Sabemos que todas as funções \(g\colon\bN\to\bC\) que satisfazem a recorrência
\begin{equation*} g(n)=5g(n-1)-6g(n-2)-4g(n-3)+8g(n-4)\quad\text{para $n\geq 3$,} \end{equation*}formam um espaço vetorial \(\mathcal F\) com as operações usuais de soma de funções e multiplicação de função por escalar complexo. Como a equação característica desta recorrência é
\begin{equation} \label{eqcarmult} x^4-5x^3+6x^2+4x-8=0\,, \end{equation}e como as raízes de \eqref{eqcarfib} são \(2\), com multiplicidade \(3\), e \(-1\), com multiplicidade \(1\), temos que as funções \(2^n\), \(n2^n\), \(n^22^n\), e \((-1)^n\) estão todas em \(\mathcal F\). Ainda, como o sistema
\begin{equation*} \left\{\begin{array}{rl} \lambda_1(-1)^0+\lambda_2 2^0+\lambda_3 0\cdot2^0 + \lambda_4 0^2\cdot2^0 = f(0)=0\\ \lambda_1(-1)^1+\lambda_2 2^1+\lambda_3 1\cdot2^1 + \lambda_4 1^2\cdot2^1 = f(1)=1\\ \lambda_1(-1)^2+\lambda_2 2^2+\lambda_3 2\cdot2^2 + \lambda_4 2^2\cdot2^2 = f(2)=2\\ \lambda_1(-1)^3+\lambda_2 2^3+\lambda_3 3\cdot2^3 + \lambda_4 3^2\cdot2^3 = f(3)=3 \end{array}\right. \end{equation*}possui a solução \(\lambda_1=-1/9,\lambda_2=1/9,\lambda_3=11/24,\lambda_4=-1/8\), temos a fórmula fechada
\begin{equation*} f(n)=\frac{-(-1)^n}9+\frac{2^n}9+\frac{11n2^n}{24}-\frac{n^22^n}8\,.\quad\scriptstyle\text{□} \end{equation*}Pré-lista de exercícios
Assim como definimos \(F_n\) como o \(n\)-ésimo número de Fibonacci, para \(n\in\bN\), podemos definir \(T_n\) como o \(n\)-ésimo número de Tribonacci, dado por:
\begin{equation*} T_n =\left\{ \begin{aligned} &F_n\,,&\quad&\text{se $n\leq 2$;}\\ &T_{n-1}+T_{n-2}+T_{n-3}\,,&\quad&\text{se $n\geq 3$.} \end{aligned} \right. \end{equation*}Encontre uma fórmula fechada para \(T_n\).
- Alice adora cantar. Ontem, ela cantou um trecho de uma ária em que as
primeiras quatro notas cantadas foram mi, ré, dó, e mi, e depois esta
sequência de quatro notas se repetiu várias vezes: mi, ré, dó, mi,
mi, ré, dó, mi, mi, ré, dó… Representando-se estas notas, da mais
aguda para a mais grave, pelas inteiros \(1\) (mi), \(0\) (ré), e \(-1\)
(dó), seja \(a_n\) o inteiro que representa a \(n\)-ésima nota cantada,
para \(n\geq 1\). Por exemplo, \(a_1=1\), \(a_2=0\), \(a_3=-1\), e assim por
diante.
- Encontre uma recorrência para \(a_n\) para \(n > 4\).
- Encontre uma fórmula fechada para \(a_n\) resolvendo a recorrência encontrada conforme os Teoremas 6.2–6.3.
- Encontre uma fórmula fechada para \(a_n\) utilizando o conceito de resto de divisão.
- Supondo que a fórmula encontrada em 2 está correta, prove por indução que a fórmula encontrada em 3 de fato corresponde à fórmula encontrada em 2, sem usar a fórmula aberta.
Considere os seguintes algoritmos para calcular o \(n\)-ésimo número de Fibonacci:
\(\underline{\text{FibonacciMuitoLento}(n)}\):
- se \(n\leq 1\), devolva \(n\);
- devolva \(\text{FibonacciMuitoLento}(n-1)+\text{FibonacciMuitoLento}(n-2)\).
\(\underline{\text{FibonacciLento}(n)}\):
- se \(n\leq 1\), devolva \(n\);
- \(a\leftarrow 0\); \(b\leftarrow 1\);
- para \(i\) de \(2\) até \(n\), faça:
- \(\quad\) \(c\leftarrow b\);
- \(\quad\) \(b\leftarrow a+b\);
- \(\quad\) \(a\leftarrow c\);
- devolva \(b\).
Qual o número, em função de \(n\), de operações aritméticas realizadas por \(\text{FibonacciMuitoLento}(n)\)? E por \({\text{FibonacciLento}(n)}\)?
- Considere a função \(f\colon \bN\to\bN\) definida por \(f(n)=n\) para todo \(n\in\bN\). Escreva uma fórmula aberta para \(f(n)\) utilizando uma recorrência linear homogênea de grau \(5\) com coeficientes constantes.
AULA 7: Análise Combinatória
DEFINIÇÃO 7.1. Seja \(A\) e \(B\) conjuntos quaisquer. Se existe bijeção entre \(A\) e \(B\), dizemos que \(A\) e \(B\) possuem a mesma cardinalidade. Em particular, quando \(A\) é um conjunto finito e \(B=\{0,1,\dotsc,n-1\}\), dizemos que a cardinalidade de \(A\) é \(n\), e escrevemos \(\lvert A\rvert=n\).
TEOREMA 7.2 (Princípio Aditivo). Sendo \(A\) e \(B\) conjuntos finitos disjuntos, \(\lvert A\cup B\rvert=\lvert A\rvert + \lvert B\rvert\).
Demonstração. Seja \(f_1\) uma bijeção de \(A\) em \(\{0,\dotsc,\lvert A\rvert - 1\}\) e seja \(f_2\) uma bijeção de \(B\) em \(\{0,\dotsc,\lvert B\rvert - 1\}\). Como a função \(f\) de \(A\cup B\) em \(\{0,\dotsc,\lvert A\rvert +\lvert B\rvert - 1\}\) definida por
\begin{equation*} f(x) = \left\{ \begin{aligned} &f_1(x)\,,&&\text{se $x\in A$,}\\ &\lvert A\rvert+f_2(x)\,,&&\text{se $x\in B$,} \end{aligned} \right. \end{equation*}é bijetiva, uma vez que \(f_1\) e \(f_2\) são bijetivas, e uma vez que \(A\) e \(B\) são disjuntos, temos que \(\lvert A\cup B\rvert=\lvert A\rvert +\lvert B\rvert\). □
TEOREMA 7.3. Sendo \(A\) e \(B\) conjuntos finitos quaisquer, \(\lvert A\setminus B\rvert=\lvert A\rvert - \lvert A\cap B\rvert\).
Demonstração. Como o conjunto \(A\) pode ser escrito como a união disjunta dos conjuntos \(A\cap B\) e \(A\setminus(A\cap B)=A\setminus B\), temos, do Teorema 7.2, que
\begin{equation*} \lvert A\rvert = \lvert A\cap B\rvert + \lvert A\setminus B\rvert\,, \end{equation*}e, portanto,
\begin{equation*} \lvert A\setminus B\rvert = \lvert A\rvert - \lvert A\cap B\rvert\,.\quad\scriptstyle\text{□} \end{equation*}TEOREMA 7.4 (Princípio da Inclusão–Exclusão). Sendo \(A\) e \(B\) conjuntos finitos quaisquer, \(\lvert A\cup B\rvert=\lvert A\rvert + \lvert B\rvert-\lvert A\cap B\rvert\).
Demonstração. Como a união \(A\cup B\) pode ser escrita como a união disjunta dos conjuntos \(A\setminus (A\cap B)\), \(B\setminus (A\cap B)\), e \(A\cap B\), temos, dos Teorema 7.2 e 7.3, que
\begin{align*} \lvert A\cup B\rvert &= \lvert A\setminus (A\cap B)\rvert+ \lvert B\setminus (A\cap B)\rvert +\lvert A\cap B\rvert\\ &= \lvert A\rvert-\lvert A\cap B\rvert +\lvert B\rvert-\lvert A\cap B\rvert +\lvert A\cap B\rvert\\ &=\lvert A\rvert +\lvert B\rvert -\lvert A\cap B\rvert\,.\quad\scriptstyle\text{□} \end{align*}DEFINIÇÃO 7.5. O conjunto dos subconjuntos de um conjunto \(A\) é chamado de conjunto das partes de \(A\) e denotado por \(2^A\). Por exemplo,
\begin{equation*} 2^{\{1,2,3\}}=\{\emptyset,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}\,. \end{equation*}TEOREMA 7.6. Sendo \(A\) um conjunto finito, \(\lvert 2^A\rvert = 2^{\lvert A\rvert}\).
Demonstração. Se \(\lvert A\rvert=0\) (i.e. se \(A=\emptyset\)), temos que \(2^A=\{\emptyset\}\) e, portanto, que \(\lvert 2^A\rvert=1=2^0\). Suponhamos, então, que \(\lvert A\rvert>0\) e, por indução no número de elementos de \(A\), que, para todo conjunto \(B\) com menos elementos que \(A\), valha que \(\lvert 2^B\rvert=2^{\lvert B\rvert}\). Ora, como supusemos \(A\neq\emptyset\), seja \(a\) um elemento de \(A\) e seja \(\mathcal S\bydef\{X\subseteq A\mathbin :a\in X\}\). Assim, \(2^A\) pode ser escrito como a união disjunta dos conjuntos \(\mathcal S\) e \(2^{A\setminus \{a\}}\). Como a todo \(X\in\mathcal S\) corresponde biunivocamente um conjunto \(Y\in 2^{A\setminus \{a\}}\), dado por \(Y\bydef X\setminus\{a\}\), temos \(\lvert\mathcal S\rvert = \lvert 2^{A\setminus \{a\}}\rvert\) e, portanto, dos Teoremas 7.2 e 7.3, e aplicando a hipótese da indução,
\begin{align*} \lvert 2^A\rvert &= \lvert \mathcal S\rvert +\lvert 2^{A\setminus \{a\}}\rvert\\ &=2\lvert 2^{A\setminus \{a\}}\rvert\\ &=2\cdot 2^{\lvert A\rvert-1}\\ &= 2^{\lvert A\rvert}\,.\quad\scriptstyle\text{□} \end{align*}TEOREMA 7.7 (Princípio da Casa dos Pombos). Sendo \(A\) e \(B\) conjuntos finitos, existe injeção de \(A\) em \(B\) se e somente se \(\lvert A\rvert\leq\lvert B\rvert\).
Demonstração. (Suficiência) Seja \(f_1\) uma injeção de \(A\) em \(B\), e seja \(f_2\) uma bijeção de \(B\) em \(\{0,\dotsc,\lvert B\rvert - 1\}\). A composição de \(f_1\) com \(f_2\) é uma injeção de \(A\) em \(\{0,\dotsc,\lvert B\rvert -1\}\) e, portanto, uma bijeção de \(A\) em \(f_2(f_1(A))\subseteq \{0,\dotsc,\lvert B\rvert - 1\}\). Consequentemente,
\begin{equation*} \lvert A\rvert=\lvert f_2(f_1(A))\rvert\leq \lvert \{0,\dotsc,\lvert B\rvert - 1\}\rvert=\lvert B\rvert\,. \end{equation*}(Necessidade) Seja \(f_1\) uma bijeção de \(A\) em \(\{0,\dotsc,\lvert A\rvert - 1\}\) e \(f_2\) uma bijeção de \(\{0,\dotsc,\lvert B\rvert - 1\}\) em \(B\). Se \(\lvert A\rvert \leq\lvert B\rvert\), temos que \(\{0,\dotsc,\lvert A\rvert - 1\}\subseteq\{0,\dotsc,\lvert B\rvert - 1\}\), e, portanto, que \(f_1\) é uma injeção de \(A\) em \(\{0,\dotsc,\lvert B\rvert - 1\}\), o que nos traz que a composição de \(f_1\) com \(f_2\) é uma injeção de \(A\) em \(B\). □
TEOREMA 7.8 (Princípio Multiplicativo). Sendo \(A\) e \(B\) conjuntos finitos quaisquer, \(\lvert A\times B\rvert=\lvert A\rvert \lvert B\rvert\).
Demonstração. Se \(\lvert A\rvert=0\), não há par ordenado \((a,b)\) que possa ser formado com \(a\in A\) e \(b\in B\); logo, \(A\times B=\emptyset\), e \(\lvert A\times B\rvert=0\), como queríamos. Suponhamos, então, que \(\lvert A\rvert > 0\) e, por indução no número de elementos de \(A\), que, para todo conjunto \(A'\) com menos elementos que \(A\), valha que \(\lvert A'\times B\rvert=\lvert A'\rvert\lvert B\rvert\).
Já que supusemos \(A\neq\emptyset\), seja \(a\) um elemento de \(A\). Como, para todo \((x,y)\in A\times B\), temos ou \(x=a\), ou \(x\neq a\), podemos escrever \(A\times B\) como a união disjunta dos conjuntos \((A\setminus\{a\})\times B\) e \(\{a\}\times B\). Assim, dos Teoremas 7.2 e 7.3,
\begin{align*} \lvert A\times B\rvert &= \lvert (A\setminus\{a\})\times B \cup \{a\}\times B\rvert\\ &= \lvert (A\setminus\{a\})\times B \rvert+\lvert \{a\}\times B\rvert\,. \end{align*}Ora, a cada \((a,b)\in\{a\}\times B\) corresponde biunivocamente um \(b\in B\). Portanto, \(\lvert \{a\}\times B\rvert = \lvert B\rvert\) e, aplicando a hipótese da indução para \((A\setminus\{a\})\times B\), temos
\begin{align*} \lvert A\times B\rvert &= \lvert (A\setminus\{a\})\times B \rvert+\lvert \{a\}\times B\rvert\\ &= \lvert (A\setminus\{a\})\rvert\lvert B \rvert+ \lvert \{a\}\rvert\lvert B\rvert\\ &= (\lvert A\rvert - 1)\lvert B \rvert+1\cdot\lvert B\rvert\\ &= \lvert A\rvert\lvert B \rvert\,.\quad\scriptstyle\text{□} \end{align*}O conjunto de todas as funções de um conjunto \(A\) em um conjunto \(B\) é denotado por \(B^A\).
TEOREMA 7.9. Sendo \(A\) e \(B\) conjuntos finitos, \(\lvert B^A\rvert = 1\) se \(A=\emptyset\), e \(\lvert B^A\rvert = \lvert B\rvert^{\lvert A\rvert}\) caso contrário.
Demonstração. Se \(\lvert A\rvert=0\), temos \(\lvert B^A\rvert=1\), pois a única função de \(A=\emptyset\) em \(B\) (mesmo quando \(B=\emptyset\)) é a relação binária \(f=\emptyset\), a qual, por vacuidade, mapeia todo elemento de \(A\) em exatamente um elemento de \(B\). Suponhamos, então, que \(\lvert A\rvert > 0\) e, por indução no número de elementos de \(A\), que, para todo conjunto \(A'\) com menos elementos que \(A\), valha que \(\lvert B^{A'}\rvert = \lvert B\rvert^{\lvert A'\rvert}\).
Já que supusemos \(A\neq\emptyset\), tomemos \(a\in A\). Para todo \(b\in B\) (se algum), seja \(S_b\bydef\{f\in B^A\mathbin : f(a)=b\}\). Evidentemente, \(B^A\) pode ser dado pela união disjunta de todos os conjuntos \(S_b\) para \(b\in B\). Ademais, para todo \(b\in B\) (se algum), a toda função \(f\in S_b\) corresponde biunivocamente uma função \(g\in B^{A\setminus \{a\}}\), a qual é dada por \(g(x)\bydef f(x)\) para todo \(x\in A\setminus\{ a\}\). Deste modo, dos Teoremas 6.2 e 6.3 e da hipótese da indução,
\begin{align*} \lvert B^A\rvert &= \biggl\lvert \bigcup_{b\in B}S_b\biggr\rvert \\ &= \sum_{b\in B}\lvert S_b\rvert \\ &= \sum_{b\in B}\lvert B^{A\setminus\{ a\}}\rvert \\ &= \sum_{b\in B} \lvert B\rvert^{\lvert A\rvert - 1} \\ &= \lvert B\rvert \lvert B\rvert^{\lvert A\rvert - 1} \\ &= \lvert B\rvert^{\lvert A\rvert}\,.\quad\scriptstyle\text{□} \end{align*}DEFINIÇÃO 7.10. Uma permutação de um conjunto finito \(A\) é uma bijeção entre \(\{0,\dotsc,\lvert A\rvert -1\}\) e \(A\). O conjunto de todas as permutações de \(A\) é denotado por \(A!\).
TEOREMA 7.11. Sendo \(A\) um conjunto finito, \(\lvert A!\rvert = \lvert A\rvert!\).
Demonstração. Se \(\lvert A\rvert=0\), a única permutação de \(A\) é a relação binária \(\pi=\emptyset\), a qual, por vacuidade, mapeia biunivocamente todo elemento de \(\{0,\dotsc,\lvert A\rvert - 1\}=\emptyset\) em exatamente um elemento de \(A\). Suponhamos, então, \(\lvert A\rvert > 0\) e, por indução em \(\lvert A\rvert\), que, para todo conjunto \(A'\) com \(\lvert A'\rvert < \lvert A\rvert\), valha que \(\lvert A'!\rvert=\lvert A'\rvert!\).
Já que supusemos \(A\neq\emptyset\), tomemos, para todo \(a\in A\), o conjunto \(S_a\bydef \{\pi\in A!\mathbin : \pi(\lvert A\rvert - 1)=a\}\). Evidentemente, o conjunto \(A!\) pode ser escrito como a união disjunta de todos os conjuntos \(S_a\) para \(a\in A\). Ademais, para todo \(a\in A\), a todo \(\pi\in S_a\) corresponde biunivocamente uma permutação de \(A\setminus\{ a\}\). Portanto, dos Teoremas 7.2 e 7.3 e da hipótese da indução,
\begin{align*} \lvert A!\rvert&= \biggl\lvert \bigcup_{a\in A}S_a\biggr\rvert\\ &= \sum_{a\in A}\lvert S_a\rvert\\ &= \sum_{a\in A} \lvert (A\setminus\{a\})!\rvert\\ &= \sum_{a\in A} (\lvert A\rvert -1)!\\ &= \lvert A\rvert (\lvert A\rvert -1)!\\ &= \lvert A\rvert!\,.\quad\scriptstyle\text{□} \end{align*}DEFINIÇÃO 7.12. O conjunto de todas as injeções de um conjunto \(A\) em um conjunto \(B\) é denotado por \(B^{\underline A}\). Quando \(A\) e \(B\) são conjuntos finitos, chamamos uma injeção de \(A\) em \(B\) de um \(A\)-arranjo de \(B\), ou simplesmente de um \(k\)-arranjo de \(B\) se \(A=\{0,\dotsc,k-1\}\) para \(k=\lvert A\rvert\).
DEFINIÇÃO 7.13. Sendo \(n\) e \(k\) inteiros não-negativos tais que \(n\geq k\), a \(k\)-ésima potência fatorial decrescente de \(n\) é o inteiro denotado e definido por:
\begin{equation*} n^{\underline k} \bydef\left\{ \begin{aligned} & 1\,,&&\text{se $k= 0$;}\\ & n\cdot (n-1)^{\underline{k - 1}}\,,&&\text{se $k > 0$.} \end{aligned} \right. \end{equation*}TEOREMA 7.14. Sendo \(A\) e \(B\) conjuntos finitos, \(\lvert B^{\underline A}\rvert = \lvert B\rvert^{\underline{\lvert A\rvert}}\) se \(\lvert A\rvert \leq\lvert B\rvert\), e \(\lvert B^{\underline A}\rvert = 0\) caso contrário.
Demonstração. Se \(\lvert A\rvert >\lvert B\rvert\), não pode haver injeção de \(A\) em \(B\) pelo Princípio da Casa dos Pombos (Teorema 7.7), e temos \(\lvert B^{\underline A}\rvert =0\) como enunciado.
Seja \(A\) um conjunto finito. Se \(\def\stirling#1#2{\genfrac\{\}{0pt}{}{#1}{#2}}\lvert A\rvert=0\), temos para todo conjunto finito \(B\) tal que \(\lvert B\rvert\geq\lvert A\rvert\), que \(\lvert B^{\underline A}\rvert=1\), pois a única função de \(A=\emptyset\) em \(B\) (mesmo quando \(B=\emptyset\)) é a relação binária \(f=\emptyset\), a qual, por vacuidade, mapeia todo elemento de \(A\) em exatamente um elemento de \(B\) e é injetiva. Suponhamos, então, que \(\lvert A\rvert > 0\) e, por indução em \(\lvert A\rvert\), que, para quaisquer conjuntos finitos \(A'\) e \(B\) com \(\lvert A'\rvert < \lvert A\rvert\leq\lvert B\rvert\), valha que \(\lvert B^{\underline{A'}}\rvert = \lvert B\rvert^{\underline{\lvert A'\rvert}}\).
Vamos mostrar que \(\lvert B^{\underline{A}}\rvert = \lvert B\rvert^{\underline{\lvert A\rvert}}\) para todo conjunto finito \(B\) tal que \(\lvert B\rvert\geq \lvert A\rvert\). Seja, para tanto, \(B\) um conjunto finito tal que \(\lvert B\rvert\geq \lvert A\rvert\). Como supusemos \(A\neq\emptyset\), tomemos \(a\in A\). Para todo \(b\in B\) (se algum), seja \(S_b\bydef\{f\in B^{\underline A}\mathbin : f(a)=b\}\). Evidentemente, \(B^{\underline A}\) pode ser dado pela união disjunta de todos os conjuntos \(S_b\) para \(b\in B\). Ademais, para todo \(b\in B\) (se algum), a toda injeção \(f\in S_b\) corresponde biunivocamente uma injeção \(g\in (B\setminus \{b\})^{\underline{A\setminus \{a\}}}\), a qual é dada por \(g(x)\bydef f(x)\) para \(x\in A\setminus\{ a\}\). Deste modo, dos Teoremas 7.2 e 7.3 e da hipótese da indução,
\begin{align*} \lvert B^{\underline A}\rvert &= \biggl\lvert \bigcup_{b\in B}S_b\biggr\rvert \\ &= \sum_{b\in B}\lvert S_b\rvert \\ &= \sum_{b\in B}\lvert ({B\setminus \{b\}})^{\underline{A\setminus\{ a\}}}\rvert \\ &= \sum_{b\in B} (\lvert B\rvert - 1)^{\underline{\lvert A\rvert - 1}} \\ &= \lvert B\rvert (\lvert B\rvert - 1)^{\underline{\lvert A\rvert - 1}} \\ &= \lvert B\rvert^{\underline{\lvert A\rvert}}\,.\quad\scriptstyle\text{□} \end{align*}DEFINIÇÃO 7.15. Sendo \(A\) um conjunto finito e \(k\) um inteiro tal que \(0\leq k\leq \lvert A\rvert\), uma \(k\)-combinação de \(A\) é um subconjunto de \(A\) com \(k\) elementos. O conjunto de todas as \(k\)-combinações de \(A\) é denotado por \(\binom A k\).
DEFINIÇÃO 7.16. Sendo \(n\) e \(k\) inteiros não-negativos satisfazendo \(0\leq k\leq n\), o coeficiente binomial \(\binom n k\), comumente lido como "\(n\) escolhe \(k\)", é o número definido por:
\begin{equation*} \binom n k \bydef \frac{n!}{k!(n- k)!}\,. \end{equation*}LEMA 7.17. Sendo \(n\) e \(k\) inteiros satisfazendo \(0 < k < n\),
\begin{equation*} \binom n k = \binom{n-1}{k-1} + \binom{n-1}k\,. \end{equation*}Demonstração. Como \(0 < k < n\), temos, da Definição 6.16, que
\begin{align*} \binom n k &= \frac{n!}{k!(n- k)!}\\ &= \frac n k\cdot\frac{ (n-1)!}{ (k-1)!(n - k)!}\\ &= \Bigl( 1 + \frac {n - k} k\Bigr)\frac{ (n-1)!}{ (k-1)!(n - k)!}\\ &= \frac{ (n-1)!}{ (k-1)!(n - k)!} + \frac{(n-k) (n-1)!}{k (k-1)!(n - k)!}\\ &= \frac{ (n-1)!}{ (k-1)!((n-1) - (k-1))!} + \frac{(n-k) (n-1)!}{k !(n - k)(n - k - 1)!}\\ &=\binom{n - 1}{k - 1}+\binom{n - 1}{k }\,.\quad\scriptstyle\text{□} \end{align*}TEOREMA 7.18. Sendo \(A\) um conjunto finito e \(k\) um inteiro tal que \(0\leq k\leq \lvert A\rvert\),
\begin{equation*} \biggl\lvert \binom A k\biggr\rvert=\binom{\lvert A\rvert}k\,. \end{equation*}Demonstração. Se \(k=0\), o conjunto \(\binom A k\) possui um único elemento, que é o conjunto vazio, e temos \(\lvert \binom A 0\rvert=1=\binom{\lvert A\rvert}0\), como queríamos. Por outro lado, se \(k=\lvert A\rvert\), o conjunto \(\binom A k\) possui também um único elemento, que é o próprio conjunto \(A\), e temos \(\lvert \binom A k\rvert=1=\binom{\lvert A\rvert}{\lvert A\rvert}\), Suponhamos, então, que \(0 < k < \lvert A\rvert\). Suponhamos também, por indução em \(\lvert A\rvert\), que, para todo \(A'\) com \(\lvert A'\rvert <\lvert A\rvert\), valha que \(\lvert \binom {A'} k\rvert=\binom{\lvert A'\rvert}k\).
Como supusemos \(A\neq\emptyset\), seja \(a\) um elemento de \(A\) e sejam \(\mathcal S_1\bydef\{X\subseteq A\mathbin :\lvert X\rvert = k\text{ e }a\notin X\}\) e \(\mathcal S_2\bydef\{X\subseteq A\mathbin :\lvert X\rvert = k\text{ e }a\in X\}\). Evidentemente, \(\binom A k\) pode ser escrito como a união disjunta dos conjuntos \(\mathcal S_1\) e \(\mathcal S_2\). Ora, como \(k < \lvert A\rvert\), o conjunto \(S_1\) é igual ao conjunto \(\binom{A\setminus\{a\}}k\), enquanto que a todo \(X\in\mathcal S_2\) corresponde biunivocamente um conjunto \(Y\in \binom{A\setminus \{a\}}{k-1}\), dado por \(Y\bydef X\setminus\{a\}\). Assim, dos Teoremas 7.2 e 7.3, do Lema 7.17, e aplicando a hipótese da indução,
\begin{align*} \biggl\lvert \binom A k\biggr\rvert &= \lvert \mathcal S_1\cup\mathcal S_2\rvert\\ &= \biggl\lvert\binom {A\setminus\{a\}}{k}\biggr\rvert+ \biggl\lvert\binom {A\setminus\{a\}}{k-1}\biggr\rvert\\ &= \binom {\lvert A\rvert - 1}{k}+ \binom {\lvert A\rvert - 1}{k-1}\\ &= \binom {\lvert A\rvert}{k}\,.\quad\scriptstyle\text{□} \end{align*}TEOREMA 7.19. Sendo \(n,k\in\bZ_{> 0}\). O número de soluções \((x_1,x_2,\dotsc,x_k)\in\bZ_{\geq 0}^k\) da equação diofantina
\begin{equation} \label{eqdiofcomb} x_1+x_2+\dotsb+x_k=n \end{equation}é \(\binom{n + k - 1}{k - 1}\).
Demonstração. Vamos primeiro mostrar que, se \(k\leq n\), então o número de soluções \((x_1,x_2,\dotsc,x_k)\in\bZ_{> 0}^k\) de \eqref{eqdiofcomb} é \(\binom{n - 1}{k - 1}\). Seja \(A=\{1,\dotsc,n-1\}\). Para qualquer solução \((x_1,x_2,\dotsc,x_k)\in\bZ_{> 0}^k\) de \eqref{eqdiofcomb}, se definimos \(y_i\bydef\sum_{j=1}^ix_j\) para \(1\leq i\leq k - 1\), temos, como \(x_j > 0\) para \(1\leq j\leq k\), que os inteiros \(y_1,y_2,\dotsc,y_{k-1} < n\) são todos distintos e, portanto, formam um subconjunto com \(k-1\) elementos de \(A\). Por outro lado, para qualquer subconjunto \(\{y_1,y_2,\dotsc,y_{k-1}\}\) com \(k-1\) elementos de \(A\) com \(y_1 < y_2 < \dotsb < y_{k-1}\), se definimos
\begin{equation*} x_i\bydef\left\{ \begin{aligned} &y_1&&\text{se $i=1$,}\\ &y_i - y_{i-1}&&\text{se $1 < i < k$,}\\ &n - y_{i-1}&&\text{se $i = k$,}\\ \end{aligned} \right. \end{equation*}temos uma solução \((x_1,x_2,\dotsc,x_k)\in\bZ_{> 0}^k\) de \eqref{eqdiofcomb}, pois
\begin{equation*} \sum_{i=1}^k x_i = y_1 + \sum_{i=2}^{k-1}(y_i - y_{i-1}) + (n - y_{k-1})=n\,. \end{equation*}Assim, a toda solução em \(\bZ_{> 0}^k\) de \eqref{eqdiofcomb} corresponde biunivocamente um conjunto em \(\binom{A}{k-1}\). Portanto, do Teorema 7.18, o número de soluções \((x_1,x_2,\dotsc,x_k)\in\bZ_{> 0}^k\) de \eqref{eqdiofcomb} é \(\binom {n - 1}{k - 1}\).
Agora, consideremos o caso em que \(n\) e \(k\) são inteiros não-negativos quaisquer. Como
\begin{equation*} x_1+x_2+\dotsb+x_k = n \end{equation*}se e somente se
\begin{equation*} (x_1+1)+(x_2+1)+\dotsb+(x_k+1) = n+k\,, \end{equation*}temos que a toda solução \((x_1,x_2,\dotsc,x_k)\in\bZ_{\geq 0}^k\) de \eqref{eqdiofcomb} corresponde biunivocamente uma solução \((y_1,y_2,\dotsc,y_k)\in\bZ_{> 0}^k\) de
\begin{equation} \label{eqdiofcomb2} y_1+y_2+\dotsb+y_k=n+k\,, \end{equation}a qual é dada por \(y_i\bydef x_i+1\) para \(1\leq i\leq k\). Portanto, como o número de soluções \((y_1,y_2,\dotsc,y_k)\in\bZ_{> 0}^k\) de \eqref{eqdiofcomb2} é \(\binom{n + k - 1}{k - 1}\), conforme já provamos, temos que este também é o número de soluções \((x_1,x_2,\dotsc,x_k)\in\bZ_{\geq 0}^k\) de \eqref{eqdiofcomb}. □
DEFINIÇÃO 7.20. Sendo \(A\) um conjunto finito e \(k\) um inteiro tal que \(0\leq k\leq \lvert A\rvert\), uma \(k\)-partição de \(A\) é uma partição \(\mathcal F\) de \(A\) tal que \(\lvert\mathcal F\rvert=k\). O conjunto de todas as \(k\)-partições de \(A\) é denotado por \(\stirling A k\).
DEFINIÇÃO 7.21. Sendo \(n\) e \(k\) inteiros não-negativos satisfazendo \(0\leq k\leq n\), o número de Stirling do segundo tipo \(\stirling n k\) é o número definido por:
\begin{equation*} \stirling n k = \left\{ \begin{aligned} & 1&&\text{se $k=n$;}\\ & 0&&\text{se $k=0 < n$;}\\ & k\stirling{n-1}k + \stirling{n-1}{k-1}&&\text{se $0 < k < n$.} \end{aligned} \right. \end{equation*}TEOREMA 7.22. Sendo \(A\) um conjunto finito e \(k\) um inteiro tal que \(0\leq k\leq \lvert A\rvert\),
\begin{equation*} \biggl\lvert \stirling A k\biggr\rvert=\stirling{\lvert A\rvert}k\,. \end{equation*}Demonstração. Se \(A=\emptyset\), temos \(k=0\) por hipótese e podemos verificar \(\stirling A k=\stirling 0 0=1\), pois, neste caso, \(\mathcal F=\emptyset\) é, por vacuidade, a única partição de \(A\) com \(\lvert \mathcal F\rvert=0\). Suponhamos, então, que \(A\neq\emptyset\). Se \(k=0\), não pode haver partição \(\mathcal F\) de \(A\) com \(\lvert \mathcal F\rvert=k\) e, portanto, \(\stirling A k=\stirling {\lvert A\rvert} 0=0\). Se \(k=\lvert A\rvert\), a única partição \(\mathcal F\) de \(A\) com \(\lvert \mathcal F\rvert=k\) é o conjunto \(\bigcup_{a\in A}\{\{a\}\}\) e, portanto, \(\stirling A k=\stirling {\lvert A\rvert} {\lvert A\rvert }=1\).
Suponhamos, agora, que \(0 < k <\lvert A\rvert\) e, por indução em \(\lvert A\rvert\), que, para todo \(A'\) com \(\lvert A'\rvert < \lvert A \rvert\) valha que \(\lvert \stirling {A'} k\rvert=\stirling{\lvert A'\rvert}k\). Sendo \(a\in A\), seja \(\mathscr L\) o conjunto de todas as partições \(\mathcal F\) com \(\lvert\mathcal F\rvert=k\) e \(\{a\}\in\mathcal F\), e seja também \(\mathscr R\) o conjunto de todas as partições \(\mathcal F\) com \(\lvert\mathcal F\rvert=k\) e \(\{a\}\notin\mathcal F\). Evidentemente, \(\stirling A k=\mathscr L\cup\mathscr R\).
Para determinarmos \(\lvert\mathscr L\rvert\), basta observar que a todo \(\mathcal F\in\mathscr L\) corresponde biunivocamente uma partição \(\mathcal G\in\stirling {A\setminus\{a\}}{k-1}\), dada por \(\mathcal G\bydef\mathcal F\setminus \{\{a\}\}\). Assim, da hipótese da indução,
\begin{equation*} \lvert\mathscr L\rvert = \biggl\lvert \stirling {A\setminus\{a\}}{k-1}\biggr\rvert =\stirling{\lvert A\rvert - 1}{k-1}\,. \end{equation*}Vamos, agora, determinar \(\lvert \mathscr R\rvert\). Para todo \(\{X_1,X_2,\dotsc,X_k\}\in\mathscr R\), temos que \(a\in X_i\) para algum \(i\in\{1,\dotsc,k\}\). Assim, \(\{X_1,\dotsc,X_i\setminus\{a\},\dotsc,X_k\}\) é uma partição em \(\stirling {A\setminus\{a\}}k\), pois \(X_1\neq\{a\}\). Por outro lado, para toda partição \(\{Y_1,\dotsc,Y_k\}\in\stirling{A\setminus\{a\}}k\), temos \(k\) partições distintas em \(\mathscr R\):
\begin{gather*} \{Y_1\cup\{a\},Y_2,\dotsc,Y_k\}\\ \{Y_1,Y_2\cup\{a\},\dotsc,Y_k\}\\ \vdots\\ \{Y_1,Y_2,\dotsc,Y_k\cup\{a\}\}\,. \end{gather*}Deste modo, a cada partição em \(\stirling{A\setminus\{a\}}k\) correspondem \(k\) partições em \(\mathscr R\) e, portanto, da hipótese da indução,
\begin{equation*} \lvert\mathscr R\rvert = k\biggl\lvert \stirling {A\setminus\{a\}}{k}\biggr\rvert =k\stirling{\lvert A\rvert - 1}k\,. \end{equation*}Logo, aplicando o Teorema 7.2 e a Definição 7.21,
\begin{align*} \biggl\lvert \stirling A k\biggr\rvert &=\lvert \mathscr L\cup\mathscr R\rvert\\ &=\stirling{\lvert A\rvert - 1}{k-1}+ k\stirling{\lvert A\rvert - 1}k\\ &= \stirling{\lvert A\rvert}k\,.\quad\scriptstyle\text{□} \end{align*}EXERCÍCIO RESOLVIDO 7.23. 208 pessoas foram à feira comprar legumes, das quais 114 compraram brócolis, 152 compraram cenoura, 28 compraram quiabo, 64 compraram brócolis e cenoura, 12 compraram somente cenoura e quiabo, 9 compraram os três vegetais. Sabendo que cada uma das 208 pessoas comprou ao menos um dos três vegetais, quantas pessoas compraram somente brócolis e quiabo?
Resolução. Sejam \(B,C,Q\) os conjuntos das pessoas que compraram brócolis, cenoura, e quiabo, respectivamente. Do Princípio da Inclusão–Exclusão, temos que
\begin{equation*} \lvert B\cup C\cup Q\rvert = \lvert B\rvert + \lvert C\rvert + \lvert Q\rvert - \lvert B\cap C\rvert - \lvert B\cap Q\rvert - \lvert C\cap Q\rvert +\lvert B\cap C\cap Q\rvert\,. \end{equation*}Do enunciado do problema, temos também:
- \(\lvert B\rvert = 114\);
- \(\lvert C\rvert = 152\);
- \(\lvert Q\rvert = 28\);
- \(\lvert B\cap C\rvert = 64\);
- \(\lvert (C\cap Q)\setminus B\rvert = \lvert C\cap Q\rvert-\lvert B\cap C\cap Q\rvert= 12\);
- \(\lvert B\cap C\cap Q\rvert = 9\), do que podemos concluir que \(\lvert C\cap Q\rvert-9= 12\) e, portanto, \(\lvert C\cap Q\rvert= 21\);
- \(\lvert B\cup C\cup Q\rvert = 208\).
Logo,
\begin{equation*} 208 = 114 + 152 + 28 - 64 - \lvert B\cap Q\rvert - 21 +9\,, \end{equation*}o que nos traz que \(\lvert B\cap Q\rvert = 10\). Queremos encontrar o número de pessoas que compraram somente brócolis e quiabo, i.e.
\begin{equation*} \lvert (B\cap Q)\setminus C\rvert =\lvert B\cap Q\rvert - \lvert B\cap C\cap Q\rvert = 10 - 9 = 1\,.\quad\scriptstyle\text{□} \end{equation*}EXERCÍCIO RESOLVIDO 7.24. Mostre que se \(51\) inteiros são escolhidos no intervalo \([1..100]\), então há dois inteiros distintos \(a\) e \(b\) dentre os escolhidos tais que \(a\) divide \(b\).
Resolução. Do Teorema Fundamental da Aritmética, sabemos que todo inteiro não-negativo \(n\) pode ser escrito da forma \(n=2^k m\) sendo \(k,m\in{\mathbb Z}_{\geq 0}\) com \(m\) ímpar. Seja \(S\) um conjunto qualquer de \(51\) inteiros selecionados no intervalo \([1..100]\). Como há somente \(50\) inteiros ímpares em \([1..100]\), temos, do Princípio da Casa dos Pombos, que deve haver dois inteiros distintos \(a,b\in S\) tais que \(a=2^{k_1}m\) e \(b=2^{k_2}m\) para o mesmo inteiro ímpar \(m\). Como \(a\neq b\), temos \(k_1\neq k_2\). Se \(k_1 < k_2\), então \(a\) divide \(b\). Se \(k_2 < k_1\), então \(b\) divide \(a\). □
EXERCÍCIO RESOLVIDO 7.25. Um anagrama de uma palavra \(x\) é uma palavra obtida permutando-se as letras de \(x\). Por exemplo, todos os \(3\) anagramas de SOS são SOS, SSO, e OSS. Quantos anagramas possui a palavra carregadores?
Resolução. Como a palavra carregadores possui comprimento \(12\), há \(12!\) permutações possíveis das posições \(1,\dotsc,12\) de suas letras. No entanto, algumas dessas permutações das posições podem gerar o mesmo anagrama, como é o caso das permutações \((8,2,\underline{3,4},5,6,7,1,9,10,11,12)\) e \((8,2,\underline{4,3},5,6,7,1,9,10,11,12)\), que geram o anagrama darregacores. Note que cada permutação \(\pi\) das posições \(1,\dotsc,12\) e cada letra \(\ell\) que ocorre \(m\) vezes na palavra induzem uma permutação das posições relativas \(1,\dotsc,m\) das ocorrências de \(\ell\) em \(\pi\). Por exemplo, na permutação \((8,2,\underline{3,4},5,6,7,1,9,10,11,12)\), a permutação das ocorrências da letra r é a permutação \((1,2,3)\), enquanto na permutação \((8,2,\underline{4,3},5,6,7,1,9,10,11,12)\), a permutação das ocorrências da letra r é a permutação \((2,1,3)\). Assim, a cada permutação das posições \(1,\dotsc,12\) corresponde biunivocamente um par \((x,y)\) em que \(x\) é um anagrama da palavra e \(y\) é a a concatenação das permutações das ocorrências das 8 letras c,a,r,e,g,d,o,s, respectivamente. Por exemplo, à permutação \((8,7,3,4,5,6,1,2,9,10,11,12)\) corresponde o anagrama darregcaores e as permutações das ocorrências dadas por
\begin{equation*} \overbrace{(1)}^{c}\overbrace{(2,1)}^{a}\overbrace{(1,2,3)}^{r} \overbrace{(1,2)}^{e}\overbrace{(1)}^{g}\overbrace{(1)}^{d}\overbrace{(1)}^{o}\overbrace{(1)}^{s}\,. \end{equation*}Logo, sendo \(P\) o conjunto das permutações das posições, \(A\) o conjunto dos anagramas, e \(C\) o conjunto das concatenações das permutações das ocorrências, temos que \(\lvert P\rvert = \lvert A \times C\lvert=\lvert A\rvert\lvert C\rvert\), \(P=\{1,\dotsc,12\}!\),
\begin{equation*} C=\{1\}!\times\{1,2\}!\times\{1,2,3\}!\times\{1,2\}!\times\{1\}!\{1\}!\{1\}!\{1\}!\,, \end{equation*}e, portanto, que
\begin{align*} \lvert P\rvert = 12! &= \lvert A\rvert\lvert C\rvert\\ &= \lvert A\rvert 1!2!3!2!1!1!1!1!\,. \end{align*}Logo,
\begin{equation*} \lvert A\rvert = \frac{12!}{1!2!3!2!1!1!1!1!}=19958400\,.\qquad\scriptstyle\text{□} \end{equation*}EXERCÍCIO RESOLVIDO 7.26. Qual o número de maneiras de distribuir mãos de \(5\) cartas de um baralho padrão de \(52\) cartas para cada um dentre \(4\) jogadores?
Resolução. Existem \(\binom{52}{5}\) maneiras de escolher a mão do primeiro jogador. Para cada uma delas, sobram \(52-5=47\) cartas no baralho, das quais escolhemos \(5\) para o segundo jogador. Portanto, para cada uma das \(\binom{52}{5}\) maneiras de escolher a mão do primeiro jogador, há \(\binom{47}{5}\) maneiras de escolher a mão do segundo jogador, para cada uma das quais há \(\binom{42}{5}\) maneiras de escolher a mão do terceiro jogador, para cada uma das quais há \(\binom{37}{5}\) maneiras de escolher a mão do quarto jogador. Do Princípio Multiplicativo, temos, portanto, que o número de maneiras de distribuir as mãos dos \(4\) jogadores é
\begin{equation*} \binom{52}5\binom{47}5\binom{42}5\binom{37}5=\frac{52!}{5!5!5!5!32!}= 1478262843475644020034240\,.\qquad\scriptstyle\text{□} \end{equation*}EXERCÍCIO RESOLVIDO 7.27. Um comitê de duas pessoas precisa ser escolhido dentre quatro matemáticos e três físicos, e precisa incluir pelo menos um matemático. De quantas maneiras esse comitê pode ser formado? A resposta é \(\binom{4}1\binom{6}1\)?
Resolução. Seja \(N_1\) o número de maneiras de formar o comitê contendo exatamente um matemático e seja o número \(N_2\) de maneiras de formar o comitê contendo dois matemáticos. Assim, a resposta é
\begin{equation*} N_1+N_2 = \binom 4 1\binom3 1 + \binom 4 2 = 18 \neq \binom 4 1\binom 6 1 = 24\,.\qquad\scriptstyle\text{□} \end{equation*}EXERCÍCIO RESOLVIDO 7.28. Quantos anagramas possui a palavra onomatopeia em que não haja ocorrências de uma mesma letra em posições adjacentes?
Resolução. Para obter, de modo único, cada anagrama de onomatopeia em que não haja ocorrências de uma mesma letra em posições adjacentes, podemos:
- começar com uma permutação das \(6\) letras que não se repetem (n, m, t, p, e, i);
- em seguida, dos \(7\) lugares que temos entre as letras, e à esquerda da
primeira e à direita da última, temos duas opções:
- escolher \(2\) deles para colocar as duas ocorrências da letra a e, em seguida, escolher \(3\) dos \(9\) lugares resultantes para colocar as três ocorrências da letra o;
- escolher \(1\) deles para colocar ambas as ocorrências da letra a, separadas por uma das ocorrências da letra o; com isso, teremos uma palavra de comprimento \(9\) e \(10\) lugares entre as letras (incluindo o lugar à esquerda da primeira e à direita da última); no entanto, \(2\) desses \(10\) lugares não podem ser escolhidos para colocarmos as ocorrências restantes da letra o, pois são os lugares à esquerda e à direita da ocorrência da letra o que usamos para separar as duas ocorrências da letra a; assim, temos que escolher \(2\) dos \(8\) lugares disponíveis para colocarmos as duas ocorrências restantes da letra o.
Com isso, temos que o número de anagramas de onomatopeia em que não haja ocorrências de uma mesma letra em posições adjacentes é:
\begin{equation*} 6!\biggl( \binom 7 2 \binom 9 3 + \binom 7 1 \binom 8 2 \biggr)=1411200\,. \end{equation*}Pré-lista de exercícios
Quantos números de 4 dígitos na base decimal terminam em 5 ou 8 de modo que a soma dos dois últimos dígitos é um número primo?
Resolução do professor. Seja \(X\) o conjunto dos números que queremos contar que terminam em 5 e seja \(Y\) o conjunto dos números que queremos contar que terminam em 8. Como \(X\) e \(Y\) são disjuntos, temos, do Princípio Aditivo, que o número de números que queremos contar é \(\lvert X\rvert+\lvert Y\rvert\). Caracterizando-se cada número que se quer contar pela tupla de seus 4 dígitos, temos que os números em \(X\) correspondem biunivocamente aos elementos de
\begin{equation*} \{1,2,3,4,5,6,7,8,9\}\times\{0,1,2,3,4,5,6,7,8,9\} \times\{0,2,6,8\}\times\{5\}\,. \end{equation*}e que os números em \(Y\) correspondem biunivocamente aos elementos de
\begin{equation*} \{1,2,3,4,5,6,7,8,9\}\times\{0,1,2,3,4,5,6,7,8,9\} \times\{3,5,9\}\times\{8\} \end{equation*}Assim, do Princípio Multiplicativo, \(\lvert X\rvert = 9\cdot10\cdot4\cdot 1=360\) e \(\lvert Y\rvert = 9\cdot10\cdot3\cdot1=270\). Portanto, o número de números que queremos contar é 630. □
De quantas maneiras podemos escolher 3 funcionários de um grupo de 25 funcionários?
Resolução do professor. Seja \(X\) o conjunto dos 25 funcionários. Cada maneira que seja quer contar é subconjunto de \(X\) com exatamente 3 elementos. Assim, o número de maneiras é
\begin{equation*} \Bigl\lvert\binom{X}{3}\Bigr\rvert=\binom{25}{3}= \frac{25\cdot24\cdot23}{3\cdot2\cdot1}=2300\,.\qquad\scriptstyle\text{□} \end{equation*}De quantas maneiras podemos escolher 3 funcionários de um grupo de 25 funcionários, para que os funcionários escolhidos ocupem cada um um cargo distinto?
Resolução do professor. Seja \(X\) o conjunto dos 25 funcionários e seja \(Y\) o conjunto dos 3 cargos. Cada maneira que se quer contar é uma injeção de \(Y\) em \(X\). Assim, o número de maneiras é
\begin{equation*} \lvert X^{\underline Y}\rvert = 25^{\underline 3} = 25\cdot 24\cdot 23 =13800\,.\qquad\scriptstyle\text{□} \end{equation*}De quantas maneiras podemos escolher funcionários de um grupo de 25 funcionários para ocuparem 3 cargos, de modo que cada cargo seja ocupado por exatamente um funcionário, mas permitindo-se que um mesmo funcionário acumule mais de um cargo?
Resolução do professor. Seja \(X\) o conjunto dos 25 funcionários e seja \(Y\) o conjunto dos 3 cargos. Cada maneira que se quer contar é uma função de \(Y\) em \(X\). Assim, o número de maneiras é
\begin{equation*} \lvert X^{Y}\rvert = 25^{3} = 25^3=15625\,.\qquad\scriptstyle\text{□} \end{equation*}- Sendo \(A\) um conjunto finito, exiba uma bijeção entre \(2^A\) e \(\{0,1\}^A\).
- Seja \(n\) um inteiro não-negativo.
- Prove que \(2^n=\sum_{k = 0}^{n}\binom n k\).
- Sendo \(k\in\bZ\) tal que \(0 \leq k\leq n\), prove que \(\binom n k=\binom{n}{n - k}\).
Sendo \(k\in\bZ\) tal que \(0 \leq k\leq n\), prove que
\begin{equation*} \binom n k = \frac{n^{\underline k}}{k!}\,. \end{equation*}Prove o Teorema Binomial, i.e. que, para quaisquer \(x,a\in\bR\),
\begin{equation*} (x+a)^n = \sum_{k=0}^n\binom n k x^{n - k}a^{k}\,. \end{equation*}
Sendo \(f\colon\bN\to\bR\), a diferença finita de \(f\) é a função definida e denotada por
\begin{equation*} \Delta f(n) \bydef f(n + 1) - f(n)\,. \end{equation*}Mostre que, para todo \(k\in\bZ_{> 0}\),
\begin{equation*} \Delta (n^{\underline k}) = k n^{\underline{k -1}}\,. \end{equation*}- Uma livraria exibe uma prateleira com cinco, três, e quatro cópias, respectivamente, dos três livros mais vendidos. Quantos maneiras diferentes há de dispor esses livros na prateleira, dado que os livros do mesmo título não podem ser distinguidos entre si?
AULA 8: Introdução a Teoria dos Grafos
DEFINIÇÃO 8.1. Um grafo simples é um par \((V,E)\), em que:
- \(V\) é o conjunto finito dos vértices do grafo;
- \(E\) é o conjunto das arestas do grafo, sendo cada aresta um par não-ordenado de vértices distintos.
Sendo \(G\) um grafo, \(V(G)\) denota o conjunto de vértices de \(G\), enquanto que \(E(G)\) denota o conjunto de arestas de \(G\). Sendo \(e\) uma aresta, formada pelos vértices \(u\) e \(v\), escrevemos \(e=uv\), e dizemos:
- que \(e\) incide em \(u\) e em \(v\);
- que \(u\) e \(v\) são os extremos, ou as extremidades, de \(e\);
- qu \(u\) e \(v\) são vizinhos, ou adjacentes.
Duas arestas são ditas adjacentes se possuem um extremo em comum. O conjunto de vizinhos de um vértice \(u\) no grafo \(G\) é o conjunto denotado e definido por \(N_G(u)\bydef \{v\mathbin : uv\in E(G)\}\). O conjunto de arestas incidentes em \(u\) em \(G\) é o conjunto denotado e definido por \(\partial_G(u)\bydef \{uv\mathbin : uv\in E(G)\}\). Para \(X\subseteq V(G)\), também definimos \(\partial_G(X)\bydef \{uv\in E(G)\mathbin: u\in X\text{ e }v\notin X\}\). Se \(0\neq X\neq V(G)\), dizemos que \(\partial_G(X)\) é o corte induzido por \(X\). O grau de \(u\) no grafo simples \(G\) é o valor denotado e definido por \(d_G(u)\bydef \lvert N_G(u)\rvert=\lvert\partial_G(u)\rvert\). O grau máximo de \(G\) é o valor denotado e definido por \(\Delta(G)\bydef \max_{u\in V(G)}d_G(u)\). O grau mínimo de \(G\) é o valor denotado e definido por \(\delta(G)\bydef \min_{u\in V(G)}d_G(u)\). Sendo \(d\in\bN\), o grafo \(G\) é dito \(d\)-regular se \(d_G(u)=d\) para todo \(u\in V(G)\). Quando livre de ambiguidade, podemos omitir \(G\) da notação, escrevendo apenas \(d(u)\), \(\partial(X)\), \(\Delta\) etc.
Neste curso, usaremos o termo grafo para nos referirmos sempre a um grafo simples.
Como exemplo, considere o grafo \(G\) definido por
\begin{align*} V(G) &= \{ a, b, c, d \}\quad\text e\\ E(G) &= \{ ab, ac, bc, bd, cd \}\,. \end{align*}Grafos podem ser representados no plano da seguinte maneira: vértices são representados por pontos, enquanto que as arestas são representadas por segmentos de curva conectando seus respectivos vértices. A seguir, apresentamos duas representações possíveis para o grafo \(G\) do exemplo. A saber, este grafo é conhecido como diamante.
TEOREMA 8.2. A soma dos graus dos vértices de um grafo \(G\) é sempre duas vezes o número de arestas de \(G\).
Demonstração. Consideremos o conjunto
\begin{equation*} X = \{ (u,e) \mathbin : u\in V(G), e\in\partial_G(u) \}\,. \end{equation*}Por um lado, cada vértice \(u\) aparece em exatamente \(\lvert \partial_G(u)\rvert=d_G(u)\) pares de \(X\); assim,
\begin{equation} \label{eqX1} \lvert X\rvert=\sum_{u\in V(G)}d_G(u)\,. \end{equation}Por outro lado, cada aresta \(e=uv\) aparece em exatamente dois pares de \(X\): os pares \((u,e)\) e \((v,e)\); assim,
\begin{equation} \label{eqX2} \lvert X\rvert =2\lvert E(G)\rvert\,. \end{equation}Combinando \eqref{eqX1} com \eqref{eqX2}, temos \(\sum_{u\in V(G)}d_G(u)=2\lvert E(G)\rvert\), como queríamos. □
LEMA 8.3 (Lema do Aperto de Mão). Em todo grafo, o número de vértices com grau ímpar é par.
Demonstração. Seja \(G\) um grafo. Seja \(X\) o conjunto dos vértices de \(G\) com grau ímpar. Do Teorema 8.2,
\begin{equation*} \sum_{u\in X}d_G(u)+\sum_{u\in V(G)\setminus X}d_G(u) = \sum_{u\in V(G)}d_G(u) = 2\lvert E(G)\rvert\,, \end{equation*}um número par. Ora, \(\sum_{u\in V(G)\setminus X}d_G(u)\) é um número par, pois é uma soma de números pares. Assim, \(\sum_{u\in X}d_G(u)\) também precisa ser um número par, o que implica, uma vez que todos os seus termos da soma \(\sum_{u\in X}d_G(u)\) são números ímpares, que o número de termos na soma \(\sum_{u\in X}d_G(u)\) é par. □
DEFINIÇÃO 8.4. Seja \(n\in\bZ_{> 0}\) e consideremos \(n\) vértices \(u_0,\dotsc,u_{n-1}\) todos distintos. O grafo completo com \(n\) vértices é o grafo denotado por \(K_n\) e definido por \(V(K_n)\bydef\{u_0,\dotsc,u_{n-1}\}\) e \(E(K_n)\bydef\{u_iu_j\mathbin : 0\leq i,j < n\}\). O caminho com \(n\) vértices é o grafo denotado por \(P_n=u_0u_1\dotsb u_{n-1}\) e definido por \(V(P_n)\bydef\{u_0,\dotsc,u_{n-1}\}\) e \(E(P_n)\bydef\{u_iu_{i+1}\mathbin : 0\leq i \leq n-2\}\), e nos referimos aos vértices \(u_0\) e \(u_{n-1}\) como os vértices externos do caminho, enquanto que aos vértices \(u_1,\dotsc,u_{n-2}\) como os vértices internos. O comprimento de um caminho \(P_n\) é seu número de arestas, i.e. \(n-1\). Para \(n\geq 3\), o ciclo de comprimento \(n\) é o grafo denotado por \(C_n=u_0u_1\dotsb u_{n-1}u_0\) e definido por \(V(C_n)\bydef\{u_0,\dotsc,u_{n-1}\}\) e \(E(C_n)\bydef\{u_iu_{(i+1)\bmod n}\mathbin : 0\leq i < n\}\). Um ciclo é dito par (ímpar) se seu comprimento é par (ímpar).
DEFINIÇÃO 8.5. Um isomorfismo de um grafo \(G\) para um grafo \(H\) é uma bijeção \(\pi\colon V(G)\to V(H)\) tal que, para quaisquer \(u,v\in V(G)\), temos \(uv\in E(G)\) se e somente se \(\pi(u)\pi(v)\in E(H)\). Se existe um isomorfismo de \(G\) para \(H\), dizemos que \(G\) e \(H\) são isomorfos.
Por exemplo, considere os seguintes grafos \(G\) e \(H\).
Estes grafos são isomorfos. Na verdade, são dois isomorfismos do grafo conhecido como grafo de Petersen. Para se observar que \(G\) e \(H\) são isomorfos, basta verificar por inspeção que a bijeção \(\pi\) definida a seguir é um isomorfismo de \(G\) para \(H\).
| \(u\in V(G)\) | \(\pi(u)\in V(H)\) |
|---|---|
| \(a\) | \(u\) |
| \(b\) | \(v\) |
| \(c\) | \(w\) |
| \(d\) | \(x\) |
| \(e\) | \(y\) |
| \(a'\) | \(u'\) |
| \(b'\) | \(v'\) |
| \(c'\) | \(w'\) |
| \(d'\) | \(x'\) |
| \(e'\) | \(y'\) |
DEFINIÇÃO 8.6. Dizemos que um grafo \(H\) é subgrafo de um grafo \(G\), e escrevemos \(H\subseteq G\), se \(V(H)\subseteq V(G)\) e \(E(H)\subseteq E(G)\). Se \(H\neq G\), dizemos que \(H\) é um subgrafo próprio de \(G\). Se \(V(H)=V(G)\), dizemos que \(H\) é um subgrafo gerador de \(G\). Sendo \(U\subseteq V(G)\), o subgrafo de \(G\) induzido por \(U\) é o grafo definido por \(V(G[U])\bydef U\) e \(E(G[U])\bydef\{uv\in E(G)\mathbin : u,v\in U\}\). Sendo \(F\subseteq E(G)\), o subgrafo de \(G\) induzido por \(F\) é o grafo definido por \(E(G[F])\bydef F\) e \(V(G[F])\bydef\{u\in V(G)\mathbin : uv\in F\text{ para algum }v\in V(G)\}\). Sendo \(u\) um vértice, definimos \(G-u\bydef G[V(G)\setminus\{u\}]\), e \(G+u\bydef (V(G)\cup\{u\}, E(G))\). Sendo \(u,v\in V(G)\), definimos \(G-uv\bydef G[E(G)\setminus\{uv\}]\), e \(G+uv\bydef (V(G),E(G)\cup\{uv\})\).
DEFINIÇÃO 8.7. Um caminho em um grafo \(G\) de um vértice \(s\) a um vértice \(t\) é um subgrafo de \(G\) isomorfo ao grafo \(P_n\), para algum \(n\in\bZ_{> 0}\), com \(s\) e \(t\) mapeados aos vértices \(u_0\) e \(u_{n-1}\), respectivamente, pelo isomorfismo. Um ciclo em \(G\) é um subgrafo de \(G\) isomorfo ao grafo \(C_n\), para algum \(n\in\bZ_{> 0}\). Se \(G\) não possui ciclos, então \(G\) é dito acíclico.
DEFINIÇÃO 8.8. Um grafo é dito conexo se, para quaisquer \(s,t\in V(G)\), existe caminho de \(s\) a \(t\). Uma componente conexa em um grafo \(G\) é um subgrafo conexo maximal de \(G\), i.e. um subgrafo conexo de \(G\) que não é subgrafo próprio de algum outro subgrafo conexo de \(G\).
TEOREMA 8.9. Seja \(G\) um grafo. As seguintes afirmações sobre \(G\) são todas equivalentes.
- \(G\) é um grafo conexo e acíclico.
- \(G\) é acíclico maximal, i.e. \(G\) é acíclico, mas não é subgrafo gerador próprio de algum outro grafo acíclico.
- \(G\) é conexo minimal, i.e. \(G\) é conexo, mas não possui subgrafo gerador próprio conexo.
- Existe um único caminho entre qualquer par de vértices de \(G\).
Demonstração. Vamos primeiro mostrar que 1 implica 2. Seja \(G\) um grafo conexo e acíclico. A fins de contradição, suponhamos que \(G\) é subgrafo gerador próprio de algum outro grafo acíclico \(\mathcal H\). Seja \(uv\in E(\mathcal H)\setminus E(G)\). Como \(G\) é conexo, existe um caminho \(ux_1\dotsb x_kv\) em \(G\), para algum \(k\geq 1\). Assim, \(ux_1\dotsb x_kvu\) é um ciclo em \(\mathcal H\), uma contradição.
Agora, vamos mostrar que 2 implica 3. Seja \(G\) um grafo acíclico maximal. Vamos primeiro mostrar que \(G\) é conexo. Suponhamos, a fins de contradição, que \(G\) tem dois vértices \(u\) e \(v\) entre os quais não há caminho. Como \(G\) é acíclico maximal, \(G+uv\) contém um ciclo \(ux_1\dotsb x_kvu\), para algum \(k\geq 1\). Logo, \(ux_1\dotsb x_kv\) é um caminho de \(u\) a \(v\) em \(G\), uma contradição. Assim, mostramos que \(G\) é conexo, mas ainda precisamos mostrar que \(G\) é conexo minimal. Suponhamos, a fins de contradição, que \(G\) possui um subgrafo gerador próprio \(H\) também conexo. Seja \(uv\in E(G)\setminus E(H)\). Como \(H\) é conexo, seja \(ux_1\dotsb x_kv\) um caminho em \(H\), para algum \(k\geq 1\). Assim, \(ux_1\dotsb x_kvu\) é um ciclo em \(G\), uma contradição, pois \(G\) é acíclico.
Para mostrarmos que 3 implica 4, seja \(G\) um grafo conexo minimal. Sabemos que, entre todo par de vértices \(u\) e \(v\) de \(G\), existe um caminho em \(G\). Suponhamos, a fins de contradição, que haja um par de vértices \(u\) e \(v\) de \(G\) para o qual haja dois caminhos distintos \(x_1\dotsb x_k\) e \(y_1\dotsb y_{\ell}\), com \(x_1=y_1=u\) e \(x_k=y_{\ell}=v\), para ambos \(k\) e \(\ell\) positivos. Podemos supor, sem perda de generalidade, que \(x_1\neq y_2\), pois, caso contrário, \(x_2\dotsb x_k\) e \(y_2\dotsb y_{\ell}\) seriam dois caminhos distintos entre \(x_2=y_2\) e \(v\), e poderíamos tomar \(u\bydef x_2=y_2\). Sejam \(i\) e \(j\) os menores inteiros diferentes de \(1\) tais que \(x_i=y_j\). Note-se que \(i\) e \(j\) estão bem definidos, pois \(x_k=y_{\ell}\). Assim, na sequência \(C=x_1x_2\dotsb x_iy_{j-1}\dotsb y_1\), temos que \(x_1=y_1\) é a única repetição. Portanto, \(C\) é um ciclo em \(G\). Assim, a remoção de qualquer aresta de \(C\), digamos \(x_1x_2\), não torna \(G\) desconexo, contradizendo que \(G\) é conexo minimal, pois em todo caminho entre um par de vértices \(a\) e \(b\) que tome a aresta \(x_1x_2\), é possível substituir \(x_1x_2\) pela sequência de vértices \(x_1y_2\dotsb y_{j-1}x_ix_{i-1}\dotsb x_2\).
Por fim, vamos mostrar que 4 implica 1. Seja \(G\) um grafo em que há um único caminho entre qualquer par de vértices. Consequentemente, \(G\) é conexo. Resta mostrar que \(G\) é também acíclico. Suponhamos, a fins de contradição, que haja um ciclo \(x_1x_2\dotsb x_kx_1\) em \(G\) para algum \(k\geq 3\). Assim, \(x_1x_2\dotsb x_k\) e \(x_kx_1\) são dois caminhos distintos entre \(x_1\) e \(x_k\) em \(G\), uma contradição. □
DEFINIÇÃO 8.10. Uma árvore é um grafo que satisfaz qualquer uma dentre (e, portanto, todas) as afirmações 1–4 do Teorema 8.9.
DEFINIÇÃO 8.11 Uma clique em um grafo \(G\) é um subconjunto de \(V(G)\) que induz um grafo completo. Um conjunto independente, ou conjunto estável, em \(G\) é um subconjunto de \(V(G)\) que induz um grafo sem arestas.
DEFINIÇÃO 8.12. Um grafo \(G\) é dito bipartido se existem dois conjuntos independentes disjuntos \(A\) e \(B\) em \(G\) tais que \(A\cup B=V(G)\), e dizemos que \(\{A,B\}\) é uma bipartição de \(G\).
TEOREMA 8.13. Um grafo é bipartido se e somente se não possui ciclos ímpares.
Demonstração. (Suficiência) Se \(G\) é um grafo bipartido, seja \(\{A,B\}\) uma bipartição de \(G\). Suponhamos que \(G\) possua um ciclo ímpar \(u_0u_1\dotsb u_{n-1}u_0\) para algum \(n\geq 3\). Suponhamos, então, sem perda de generalidade, que \(u_0\in A\), o que implica que \(u_1\in B\) e, portanto, que \(u_2\in A\) e, assim sucessivamente, que \(u_{n-1}\in A\) e, portanto, que \(u_0\in B\), uma contradição.
(Necessidade) Seja \(G\) um grafo sem ciclos ímpares. Se \(G\) não possui vértices, então é bipartido por satisfazer a Definição 8.12 por vacuidade. Sejam, portanto, \(C_1,\dotsc,C_k\) as componentes conexas de \(G\), para algum \(k\geq 1\). Como uma árvore é um grafo conexo minimal, sejam \(T_1,\dotsc,T_k\) árvores geradoras de \(C_1,\dotsc,C_k\), respectivamente. Sejam também \(r_1,\dotsc,r_k\) vértices quaisquer de \(C_1,\dotsc,C_k\), respectivamente. Para todo \(i\in\{1,\dotsc,k\}\) e todo \(u\in C_i\), seja \(h(u)\) o comprimento do único caminho entre \(u\) e \(r_i\) em \(T_i\). Sejam \(A\bydef \{u\in V(G)\mathbin : h(u)\text{ é par}\}\) e \(B\bydef \{u\in V(G)\mathbin : h(u)\text{ é ímpar}\}\). Por construção, \(A\) e \(B\) são disjuntos, e \(A\cup B=V(G)\). Observe-se ainda que, para qualquer caminho \(x_1\dotsb x_k\) em alguma árvore \(T_i\), não há dois vértices adjacentes no caminho que pertençam ambos a \(A\) ou ambos a \(B\).
Vamos mostrar que \(\{A,B\}\) é uma bipartição de \(G\). Suponhamos, a fins de contradição, que \(A\) ou \(B\) não seja um conjunto independente e, assim, tomemos uma aresta \(uv\in A\), sem perda de generalidade. Seja \(C_i\) a componente à qual \(u\) e \(v\) pertencem. Como ambos \(h(u)\) e \(h(v)\) são pares, \(u\) e \(v\) não são vizinhos em \(T_i\). Seja \(ux_1\dotsb x_kv\) um caminho entre \(u\) e \(v\) em \(T_i\), para algum \(k\geq 1\). Como não há dois vértices adjacentes no caminho que pertençam ambos a \(A\) ou ambos a \(B\), temos, para \(1\leq j\leq k\), que \(x_j\in A\) se \(i\) é par, e \(x_j\in B\) se \(i\) é ímpar. Assim, \(k\) é ímpar e, portanto, \(ux_1\dotsb x_kv\) é um caminho com número ímpar de vértices. Logo, \(ux_1\dotsb x_kvu\) é um ciclo ímpar em \(G\), uma contradição. □
AULA 9: Enumerabilidade
- Base: [Vel06] Sec. 7.1–7.2
DEFINIÇÃO 9.1 Um conjunto \(A\) é dito enumerável, ou discreto, se ou é um conjunto finito, ou pode ser posto em correspondência biunívoca com \(\def\bN{\bZ_{\geq 0}}\bN\). Tal correspondência é dita uma enumeração de \(A\).
TEOREMA 9.2 O conjunto dos inteiros não-negativos pares é enumerável.
Demonstração. Seja \(f\colon \bN\to2\bN\) a função definida por \(f(n)\def\bydef{\mathbin{:=}}\bydef 2n\). Se \(n_1,n_2\in\bN\), temos que \(2n_1=2n_2\) só se \(n_1=n_2\); portanto, \(f\) é injetiva. Se \(n\in2\bN\), então \(f(n/2)=n\); portanto, \(f\) é sobrejetiva. Logo, \(f\) é uma bijeção entre \(\bN\) e \(2\bN\), i.e. \(2\bN\) é enumerável. □
TEOREMA 9.3. O conjunto dos inteiros é enumerável.
Demonstração. Seja \(f\colon\bZ\to\bN\) a função definida por
\begin{equation*} f(z)\bydef\left\{ \begin{aligned} & 2z\,,&&\text{se $z\geq 0$;}\\ & -2z-1\,,&&\text{se $z < 0$.} \end{aligned} \right. \end{equation*}Se \(z_1\in\bN\) e \(z_2\in\bZ_{< 0}\), temos que \(f(z_1)\) é um número par, enquanto que \(f(z_2)\) é um número ímpar. Se ambos \(z_1,z_2\in\bN\), temos que \(f(z_1)=2z_1=f(z_2)=2z_2\) somente se \(z_1=z_2\). Se ambos \(z_1,z_2\in\bZ_{< 0}\), temos que \(f(z_1)=-2z_1-1=f(z_2)=-2z_2-1\) somente se \(z_1=z_2\). Portanto, \(f\) é injetiva. Por outro lado, para todo \(n\in\bN\), temos que: se \(n\) é par, então \(f(n/2)=n\); se \(n\) é ímpar, então \(f(-(n+1)/2)=n\). Portanto, \(f\) é também sobrejetiva. Logo, \(f\) é uma bijeção entre \(\bZ\) e \(\bN\), i.e. \(\bZ\) é enumerável. □
COROLÁRIO 9.4. A união de dois conjuntos enumeráveis é um conjunto enumerável.
Demonstração. Sejam \(A\) e \(B\) dois conjuntos enumeráveis e sejam, portanto, \(f_A\colon A \to\bN\) e \(f_B\colon B\to\bN\) duas bijeções. Assim, a função \(g\colon B\to{\mathbb Z}_{> 0}\) dada por \(g(b)=-f_B(b)-1\), para todo \(b\in B\), é também uma bijeção. Logo, a função \(h\colon A\cup B\to\bZ\) dada por
\begin{equation*} h(x)\bydef\left\{ \begin{aligned} & f_A(x)\,,&&\text{se $x\in A$,}\\ & g(x)\,,&&\text{se $x\in B$,} \end{aligned} \right. \end{equation*}é também uma bijeção. Como \(\bZ\) é enumerável pelo Teorema 9.3, temos que \(A\cup B\) é enumerável. □
No Lema 9.5, para mostrarmos que o conjunto \(\bN^2\) é enumerável, usamos um triângulo numérico chamado, às vezes, de Triângulo de Cantor, o qual satisfaz as seguintes propriedades:
- os elementos desse triângulo são todos os pares de inteiros não-negativos;
- cada \(i\)-ésima linha do triângulo, contando-se as linhas a partir de \(i=0\), reúne todos os pares \((a,b)\) tais que \(a+b=i\), começando com o par \((i,0)\) e terminando com o par \((0,i)\).
As primeiras linhas do Triângulo de Cantor são exibidas a seguir.
\begin{equation*} \begin{array}{} (0,0)&&&&&\\ (1,0) & (0,1)&&&&\\ (2,0) & (1,1) & (0,2) &&&\\ (3,0) & (2,1) & (1,2) & (0,3)&&\\ (4,0) & (3,1) & (2,2) & (1,3) & (0,4) &\\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{array} \end{equation*}LEMA 9.5. O conjunto \(\bN^2\) é enumerável.
Demonstração. Seja \(f\colon \bN^2\to\bN\) a função que determina a posição de cada par \((a,b)\in\bN^2\) no Triângulo de Cantor quando concatenamos todas as linhas do triângulo, i.e.
\begin{equation*} f(a, b) = \left\{ \begin{aligned} & 0\,,&&\text{se $a=b=0$;}\\ & f(a - 1, 0) + a\,,&&\text{se $a > 0$ e $b=0$;}\\ & f(a + b, 0) + b\,,&&\text{se $b > 0$.} \end{aligned} \right. \end{equation*}Observe-se que a função \(f\) está bem definida, uma vez que a recorrência
\begin{equation*} f(a, 0)=f(a - 1, 0) + a \end{equation*}define \(f\) para todo \(a\in\bN\), e a recorrência
\begin{equation*} f(a, b)=f(a+b, 0) + b \end{equation*}define \(f\) para quaisquer \(a,b\in\bN\), já que \(f(a+b,0)\) está definida.
Por construção, \(f(a,b)=f(c,d)\) só se \(a+b=c+d\). Como \(f(a_1,0)=f(a_2,0)\) só se \(a_1=a_2\), temos \(f(a,b)=f(c,d)\) só se \((a,b)=(c,d)\). Por outro lado, para todo \(n\in\bN\), vamos mostrar que existe um par \((a,b)\in\bN^2\). Como
\begin{equation*} f(a, 0)=\sum_{i=0}^ai=\frac{a(a+1)}2\quad\text{para todo $a\in\bN$,} \end{equation*}temos que \(f(a,0)=n\) se \(a=(\sqrt{1+8n}-1)/2\). Portanto, \(f(a,b)=f(a+b, 0) + b=n\) se \(a+b=\lfloor(\sqrt{1+8n}-1)/2\rfloor\). Assim, para todo \(n\in\bN\), se definimos \(r\bydef \lfloor(\sqrt{1+8n}-1)/2\rfloor\), temos, para
\begin{align*} b &= n-\frac{r(r+1)}2\quad\text{e}\\ a &= r-b\,, \end{align*}que \(f(a,b)=n\). Logo, \(f\) é bijetiva. □
TEOREMA 9.6. O conjunto dos números racionais é enumerável.
Demonstração. Vamos primeiro mostrar que existe bijeção entre \(\bN\) e \(\def\bQ{\mathbb Q}\bQ_{\geq 0}\). Para tanto, pelo Teorema de Cantor–Schröder–Bernstein (Teorema 9.13), é suficiente mostrar que existem injeções de \(\bN\) em \(\bQ_{\geq 0}\) e de \(\bQ_{\geq 0}\) em \(\bN\).
Como \(\bN\subseteq\bQ\), a relação identidade é uma injeção de \(\bN\) em \(\bQ\). Vamos mostrar que existe injeção de \(\bQ_{\geq 0}\) em \(\bN\). Seja \(f\colon \bQ_{\geq 0}\to\bN^2\) a função definida por: se \(q=0\), então \(f(q)=(0,0)\); se \(q > 0\), então \(f(q)\) é o par \((a,b)\) em que \(a\) e \(b\) são os únicos inteiros coprimos tais que \(q=a/b\). Por construção, \(f\) é injetiva. Como, do Lema 9.5, existe uma bijeção \(g\) de \(\bN^2\) em \(\bN\), temos que a composição de \(f\) com \(g\) é uma injeção de \(\bQ_{\geq 0}\) em \(\bN\), como queríamos.
Como mostramos que \(\bQ_{\geq 0}\) é um conjunto enumerável, seja \(h\) uma bijeção de \(\bQ_{\geq 0}\) em \(\bN\). A função \(h'\colon\bQ_{\leq 0}\to\bN\) definida por \(h'(q)=h(-q)\) é também uma bijeção. Assim, \(\bQ_{\leq 0}\) e \(\bQ_{\geq 0}\) são ambos enumeráveis, e a demonstração se conclui pelo Corolário 9.4. □
TEOREMA 9.7. O conjunto \(\{0,1\}^{\bN}\) não é enumerável.
Demonstração (Argumento da Diagonal de Cantor). Suponhamos que \(\{0,1\}^{\bN}\) seja enumerável. Sejam, então, \(s_0,s_1,s_2,\dotsc\) os elementos de \(\{0,1\}^{\bN}\). Para cada \(s_i\) e cada \(j\in\bN\), seja \(s_{ij}\bydef s_i(j)\). Seja, então, \(x\colon \bN\to\{0,1\}\) a função definida por
\begin{equation*} x_j\bydef x(j) \bydef \overline{s_{jj}}\quad\text{para todo $j\in\bN$,} \end{equation*}sendo \(\overline{s_{jj}}\) o complemento de \(s_{jj}\), i.e. \(\overline{s_{jj}}=1\) se \(s_{jj}=0\), e \(\overline{s_{jj}}=0\) se \(s_{jj}=1\). Como \(x\in\{0,1\}^{\bN}\), existe algum \(i\in\bN\) tal que \(x=s_i\), o que implica \(x_i=s_{ii}\). No entanto, por construção, \(x_i=\overline{s_{ii}}\), uma contradição. □
COROLÁRIO 9.8. Os conjuntos \(2^{\bN}\) e \(\def\bR{\mathbb R}\bR\) não são enumeráveis.
Demonstração. Vamos primeiro mostrar que o conjunto \(2^{\bN}\) não é enumerável. Seja \(f\colon 2^{\bN}\to \{0,1\}^{\bN}\) a função definida por: para todo \(X\subseteq \bN\), \(f(X)\) é a função \(f_X\colon\bN\to\{0,1\}\) definida por: \(f_X(n)=1\) se \(n\in X\); \(f_X(n)=0\) se \(n\notin X\). Por construção, a cada \(X\subseteq \bN\) corresponde biunivocamente uma única função \(f_X\in\{0,1\}^{\bN}\). Portanto, \(f\) é uma bijeção entre \(2^{\bN}\) e \(\{0,1\}^{\bN}\). Como \(\{0,1\}^{\bN}\) não é enumerável pelo Teorema 9.7, temos que \(2^{\bN}\) também não é enumerável.
Agora, vamos mostrar que o conjunto \(\bR\) não é enumerável. Seja \(\def\uppi{\text{π}}f\colon(0,1)\to(-\uppi/2,\uppi/2)\) a função definida por \(f(x)=\uppi x -\uppi/2\). Por construção, \(f\) é uma bijeção entre \((0,1)\) e \((-\uppi/2,\uppi/2)\). Como a função \(\tan\) é uma bijeção entre \((-\uppi/2,\uppi/2)\) e \(\bR\), temos que \(f\circ\tan\) é uma bijeção entre \((0,1)\) e \(\bR\). Seja \(g\colon(0,1)\to\{0,1\}^{\bN}\) a função que mapeia \(x\in(0,1)\) para a única sequência \(s_0s_1s_2\dots\{0,1\}^{\bN}\) que satisfaz \(x = \sum_{i=1}^{\infty}s_i2^{-i}\). Note-se que \(g\) é uma bijeção entre \([0,1]\) e \(\{0,1\}^{\bN}\). Assim, temos injeção de \(\{0,1\}^{\bN}\) em \(\bR\) (a composição da bijeção de \(\{0,1\}^{\bN}\) em \([0,1]\) com o mapeamento identidade de \([0,1]\) em \(\bR\)) e injeção de \(\bR\) em \(\{0,1\}^{\bN}\) (a composição da bijeção de \(\bR\) em \((0,1)\) com o mapeamento identidade de \((0,1)\) em \([0,1]\) e com a bijeção de \([0,1]\) em \(\{0,1\}^{\bN}\)). Portanto, do Teorema de Cantor–Schröder–Bernstein, temos bijeção entre \(\bR\) em \(\{0,1\}^{\bN}\). Logo, como, do Teorema 9.7, \(\{0,1\}^{\bN}\) não é enumerável, \(\bR\) também não o é. □
TEOREMA 9.9 (Teorema de Cantor). Para todo conjunto \(A\), não há bijeção entre \(A\) e \(2^A\).
Demonstração (Argumento da Diagonal de Cantor). Suponhamos que exista um conjunto \(A\) para o qual exista uma bijeção \(f\) de \(A\) para \(2^A\). Claramente, \(A\) é infinito, pois do contrário,
\(\lvert 2^A\rvert=2^{\lvert A\rvert} > \lvert A\rvert\), mesmo quando \(A=\emptyset\). Seja, então, \(T\bydef\{a\in A\mathbin: a\notin f(a)\}\). Como \(A\neq\emptyset\), \(T\in 2^A\), e \(f\) é uma bijeção, temos que existe um único \(t\in A\) tal que \(f(t)=T\). Temos dois casos:
- se \(t\in T\), então não vale que \(t\notin f(t)\) e, pela construção de \(T\), temos \(t\notin T\);
- se \(t\notin T\), então \(t\notin f(t)\) e, pela construção de \(T\), temos \(t\in T\).
Como chegamos a uma contradição em ambos os casos, temos que a bijeção \(f\) não pode existir. □
Uma das coisas intrigantes sobre o conjunto dos racionais ser enumerável, não contínuo (como o conjunto dos reais), é que entre quaisquer racionais \(q_1,q_2\) existe um terceiro racional: \((q_1+q_2)/2\). Algo ainda mais intrigante é provado a seguir.
TEOREMA 9.10. Entre quaisquer números reais \(a,b\) há um número racional \(q\) distinto de ambos \(a,b\).
Demonstração. Suponhamos sem perda de generalidade que \(a < b\) e tomemos \(n\) como o menor inteiro positivo tal que \(n(b - a) > 1\), o qual certamente existe, já que \(b-a>0\) e, portanto, que \(\lim_{n\to\infty} n(b - a)=\infty\). Tomemos
\begin{equation*} m \coloneqq \left\{ \begin{aligned} & \lfloor nb\rfloor\,,&&\text{se $nb$ não é um inteiro;}\\ & \lceil na\rceil\,,&&\text{caso contrário.} \end{aligned} \right. \end{equation*}Assim, como \(nb - na > 1\), temos que \(m\) é um inteiro que satisfaz \(na < m < nb\). Logo, tomando o racional \(q=m/n\), temos \(a < q < b\), como queríamos. □
O Argumento da Diagonal de Cantor, presente nas demonstrações dos Teoremas 9.7 e 9.9, é também presente até mesmo em alguns paradoxos. Na Teoria Ingênua dos Conjuntos, não há restrição alguma sobre um conjunto poder ser elemento de si mesmo, o que gera o seguinte paradoxo.
PARADOXO 9.11 (Paradoxo de Russell). Seja \(\mathcal M=\{X\mathbin : X\notin X\}\). Vamos mostrar que não vale nem que \(\mathcal M\in\mathcal M\), nem que \(\mathcal M\notin\mathcal M\). Se \(\mathcal M\in\mathcal M\), então \(\mathcal M\) não satisfaz a condição da construção de \(\mathcal M\), logo \(\mathcal M\notin\mathcal M\), o que é uma contradição. Por outro lado, se \(\mathcal M\notin \mathcal M\), então \(\mathcal M\) satisfaz a condição da construção de \(\mathcal M\), logo \(\mathcal M\in\mathcal M\), o que também é uma contradição.
O Argumento da Diagonal também está presente nas provas de teoremas importantes da Matemática do séc. XX, como os Teoremas da Incompletude de Gödel (1931) e o Teorema da Indecidibilidade de Problema da Parada (Turing, 1936). Dos Teoremas da Incompletude de Gödel, tem-se que a partir de qualquer conjunto finito de axiomas que se tome, sempre vai haver proposições indecidíveis, i.e. proposições que não podem nem ser mostradas verdadeiras, nem falsas. Um exemplo de proposição indecidível para os conjuntos de axiomas comumente aceitos para definir as bases da Matemática (denotados por ZF ou ZFC), é a Hipótese do Contínuo, como explanado a seguir.
Sendo \(X\) um conjunto infinito, escrevemos \(\lvert X\rvert=\aleph_0\) para indicar que existe bijeção entre \(X\) e \({\mathbb Z}_{\geq 0}\). Escolhemos essa notação porque para todo subconjunto \(Y\) infinito de \({\mathbb Z}_{\geq 0}\), existe bijeção entre \(Y\) e \({\mathbb Z}_{\geq0}\) (Exercício 2). Nesse sentido, \(\aleph_0\) é o menor dos cardinais infinitos. Conforme mostramos, \(\lvert {\mathbb Z}_{\geq 0}\rvert=\lvert \mathbb Z\rvert=\lvert\mathbb Q\rvert = \aleph_0\). Por outro lado, escrevemos \(\lvert X\rvert=2^{\aleph_0}\) para indicar que existe bijeção entre \(X\) e \(2^{{\mathbb Z}_{\geq0}}\), e, neste caso, dizemos que \(X\) é contínuo. Conforme mostramos no Corolário 9.8, \(\lvert 2^{{\mathbb Z}_{\geq 0}}\rvert=\lvert \{0,1\}^{{\mathbb Z}_{\geq 0}}\rvert=\lvert\mathbb R\rvert = 2^{\aleph_0}\). Será que existe algum cardinal maior que \(\aleph_0\) (a cardinalidade dos conjuntos infinitos enumeráveis) e menor que \(2^{\aleph_0}\) (a cardinalidade dos conjuntos contínuos)? Isto é, será que existem conjuntos \(A,B,C\) tais que \(A\subseteq B\subseteq C\), \(\lvert A\rvert=\aleph_0\), \(\lvert C\rvert=2^{\aleph_0}\), mas \(B\) não pode ser colocado em correspondência biunívoca nem com \(A\), nem com \(C\)? Veja que a resposta negativa dessa pergunta é a afirmação de que o próximo cardinal estritamente maior que \(\aleph_0\) seria \(2^{\aleph_0}\), e, neste caso, poderíamos escrever \(2^{\aleph_0}=\aleph_1\), conforme enunciado na seguinte proposição.
HIPÓTESE 9.12 (Hipótese do Contínuo). \(2^{\aleph_0}=\aleph_1\).
Como comentamos acima, a Hipótese do Contínuo é indecidível, i.e. já foi provado (Gödel, 1940; Cohen, 1963) que, com o conjunto de axiomas que usamos para definir as bases da Matemática, é impossível tanto provarmos quanto refutarmos a Hipótese do Contínuo.
Leitura complementar: o Teorema de Cantor–Schröder–Bernstein
É fácil provar que se existe injeção de um conjunto \(A\) para um conjunto \(B\), então existe uma sobrejeção de \(B\) para \(A\). Não é difícil ver também que, para o caso de \(A\) e \(B\) serem conjuntos finitos, se existe injeção de \(A\) para \(B\) e se existe injeção de \(B\) para \(A\), então existe bijeção entre \(A\) e \(B\). O teorema a seguir nos traz a validade desta implicação mesmo no caso de \(A\) e \(B\) infinitos.
TEOREMA 9.13 (Teorema de Cantor–Schröder–Bernstein). Sendo \(A\) e \(B\) conjuntos quaisquer, se há injeção de \(A\) em \(B\) e se há injeção de \(B\) em \(A\), então há bijeção entre \(A\) e \(B\).
Demonstração. Sejam \(f\colon A\to B\) e \(g\colon B\to A\) injeções e sejam os subconjuntos \(C_0,C_1,C_2,\dotsc\) de \(A\) definidos por:
\begin{equation} C_j\bydef\left\{ \begin{aligned} & A\setminus g(B)\,,&&\text{se $j=0$;}\\ & g(f(C_{j-1}))\,,&&\text{se $j>0$.} \end{aligned} \right. \label{eqCj} \end{equation}Desta forma, tomemos \(C\bydef\bigcup_{j\geq 0}C_j\subseteq A\) e definamos uma função \(h\colon A\to B\) por:
\begin{equation*} h(a)\bydef\left\{ \begin{aligned} & f(a)\,,&&\text{se $a\in C$;}\\ & g^{-1}(a)\,,&&\text{se $a\notin C$.} \end{aligned} \right. \end{equation*}Note-se que \(h\) está bem definida, pois se \(a\notin C\), então \(a\notin C_0\) e, portanto, \(a\in g(B)\) e existe \(g^{-1}(a)\).
Vamos mostrar que \(h\) é injetiva. Sejam \(a_1\) e \(a_2\) elementos distintos de \(A\).
Se ambos \(a_1,a_2\in C\), então
\begin{equation*} h(a_1)=f(a_1)\neq f(a_2)=h(a_2)\,, \end{equation*}uma vez que \(f\) é injetiva.
Se ambos \(a_1,a_2\notin C\), então
\begin{equation*} h(a_1)=g^{-1}(a_1)\neq g^{-1}(a_2)=h(a_2)\,, \end{equation*}uma vez que \(g\) é injetiva.
Agora, se um entre \(a_1\) e \(a_2\) está em \(C\) e o outro não, então, supondo sem perda de generalidade que \(a_1\in C\) e \(a_2\notin C\), suponhamos a fim de contradição que
\begin{equation*} h(a_1)=f(a_1)=g^{-1}(a_2)=h(a_2)\,. \end{equation*}Ora, se \(a_1\in C\), então \(a_1\in C_i\) para algum \(i\geq 0\) por definição. Assim, por \eqref{eqCj}, temos que \(g(f(a_1))\in C_{i+1}\). Porém, como \(f(a_1)=g^{-1}(a_2)\), isto significa que \(g(g^{-1}(a_2))=a_2\in C_{i+1}\), um absurdo, já que \(a_2\notin C\).
Para concluirmos a demonstração, vamos mostrar que \(h\) é sobrejetiva. Para tanto, tomemos \(b\in B\). Se \(b\in f(C)\), então existe algum \(a\in C\) tal que \(f(a)=b=h(a)\). Por outro lado, se \(b\notin f(C)\), tomemos \(a=g(b)\). Sabemos que \(a\notin C_0\), pois \(a\in g(B)\). Se, porventura, \(a\in C_i\) para algum \(i>0\), teríamos que \(a\in g(f(C_{i-1}))\) e, como \(g\) é injetiva, que \(b\in f(C_{i-1})\subseteq f(C)\), uma contradição que nos leva a concluir que \(a\notin C_i\) para todo \(i>0\). Logo, \(a\notin C\), o que nos traz que
\begin{equation*} h(a)=g^{-1}(a)=g^{-1}(g(b))=b\,. \end{equation*}Assim mostramos que para todo \(b\in B\) há um \(a\in A\) tal que \(h(a)=b\). □
Pré-lista de exercícios
- Um conjunto finito não-vazio é, às vezes, chamado de alfabeto. Uma palavra sobre \(\Sigma\) é uma sequência finita de elementos de um alfabeto \(\Sigma\). Uma linguagem sobre \(\Sigma\) é um conjunto (finito ou infinito) de palavras sobre \(\Sigma\). Sendo \(\Sigma^{\ast}\) o conjunto de todas as palavras sobre \(\Sigma\), mostre que \(\Sigma^{\ast}\) é enumerável, mas que o conjunto de todas as linguagens sobre \(\Sigma\) não o é.
- Mostre que todo subconjunto de um conjunto enumerável é também enumerável.
- Para todo estudante \(x\), seja \(H(x)\) o conjunto de todos os estudantes de quem \(x\) faz o dever de casa. Mostre que não pode haver um estudante \(x\) tal que \(H(x)\) seja o conjunto de todos os estudantes que não fazem seu próprio dever de casa.
- Utilize indução e o Triângulo de Cantor, nos moldes do Lema 9.5, para mostrar que uma união enumerável de conjuntos enumeráveis é também um conjunto enumerável.
- Para todo \(\mathcal F\subseteq \bR^{\bZ_{> 0}}\), mostre que, se \(\mathcal F\) é enumerável, então existe uma função \(g\in\def\bR^{\bZ_{> 0}}\) tal que \(f(n)=O(g(n))\) para todo \(f\in\mathcal F\).
Lista de exercícios
- Mostre que \(0\) divide um número inteiro \(z\) se e somente se \(z=0\).
- Mostre que, sendo \(x\) e \(y\) números reais, se \(x+y\geq 2\), então \(x\geq 1\) ou \(y\geq 1\).
- ★Mostre que o quadrado de um inteiro ímpar sempre pode ser escrito como \(8k +1\) para algum inteiro \(k\). Mostre também que o quadrado de um inteiro par sempre pode ser escrito ou como \(8k\), ou como \(8k+4\), para algum inteiro \(k\).
- Embora \(A\Rightarrow B\) e \(\neg B\Rightarrow\neg A\) sejam equivalentes, nem
sempre que vale \(A\Rightarrow B\), vale \(B\Rightarrow A\). Para cada
uma das equivalências a seguir, prove ambas suficiência e
necessidade, ou refute ambas, ou prove uma e refute a outra.
- O quadrado de um número inteiro \(a\) é par se e somente se \(a\) é par.
- O quadrado de um número inteiro \(a\) é divisível por \(3\) se e somente se \(a\) é divisível por \(3\).
- O quadrado de um número inteiro \(a\) é divisível por \(4\) se e somente se \(a\) é divisível por \(4\).
- Mostre que \(\sqrt 3\) é um número irracional.
- ★Dois números inteiros \(a\) e \(b\) são ditos coprimos se
\(1\) é o maior inteiro que divide ambos \(a\) e \(b\). Mostre que:
- o único divisor positivo de \(1\) é o próprio número \(1\);
- \(0\) e \(1\) são números coprimos;
- sendo \(k,a,b\) inteiros, se \(k\) divide ambos \(a\) e \(a+b\), então \(k\) divide \(b\);
- para todo inteiro não-negativo \(a\), são primos entre si \(a\) e \(a+1\).
- ★Mostre que, ao dispor os \(10\) primeiros inteiros
positivos numa circunferência, em qualquer ordem, sempre se obtém
três desses números em posições consecutivas cuja soma é pelo menos
\(17\). Dicas:
- prove primeiro, como um lema, que, em qualquer sequência finita \(X\) de números reais, sempre existe um elemento não menor que a média aritmética simples de todos os números em \(X\);
- agora, dispondo-se os \(10\) primeiros inteiros positivos numa circunferência, em qualquer ordem, e tomando \(X\) como o conjunto dos valores da soma de cada tripla de números em posições consecutivas, o que podemos afirmar sobre a média dos números em \(X\)?
- Mostre por indução que, para todo inteiro
não-negativo \(n\), vale que:
- \(\sum_{i=0}^n i^2=n(n+1)(2n+1)/6\);
- \(\sum_{i=0}^n i^3=\bigl(\sum_{i=0}^n i\bigr)^2\);
para todo real \(x\) diferente de \(0\) e de \(1\),
\begin{equation*} \sum_{i=0}^n x^i = \frac{x^{n+1}-1}{x-1}\,; \end{equation*}- a soma dos \(n\) primeiros inteiros positivos ímpares é igual a \(n^2\).
- ★Sendo \(n\) um inteiro positivo, seja \(H_n\) o \(n\)-ésimo número harmônico, i.e.
\(H_n=\sum_{i=1}^n\frac 1i\). Mostre, para todo inteiro positivo
\(n\), que:
- \(H_{2^n}\leq 1 + n\);
- \(H_1+H_2+\dotsb+H_n=(n+1)H_n-n\).
★Seja \(X_n\), para \(n\) inteiro não-negativo, definido por:
\begin{equation*} X_n =\left\{ \begin{aligned} &n\,,&\quad&\text{se $n\leq 2$;}\\ &2X_{n-2}+X_{n-3}\,,&\quad&\text{se $n\geq 3$.} \end{aligned} \right. \end{equation*}Mostre por indução que, para todo inteiro não-negativo \(n\),
\begin{equation*} X_n = (-1)^n-(\upphihat\cdot \upphi^n + \upphi\cdot\upphihat^n)\,. \end{equation*}★Mostre, para todo inteiro positivo \(n\), que:
- \(2^{2n}-1\) é divisível por \(3\).
- \(4^{n+1}+5^{2n-1}\) é divisível por \(21\);
- \(11^{n+1}+12^{2n-1}\) é divisível por \(133\).
Dicas: que relação \(4\) e \(21\) têm com \(5\), que \(11\) e \(133\) também têm com \(12\)?
- Mostre por indução a Desigualdade de Bernoulli, que asserta que, para todo inteiro não-negativo \(n\) e todo real \(h > -1\), vale que \((1+h)^n\geq 1 + nh\).
- Prove ou refute: Sendo \(n\) um inteiro positivo e \(p_1,p_2,\dotsc,p_n\) os primeiros \(n\) números primos, \(p_1\times p_2\times \dotsb\times p_n+1\) é um número primo.
- Mostre que, sendo \(a\), \(b\), e \(c\) inteiros tais que \(a\) divide \(bc\), se \(a\) e \(b\) são coprimos, então \(a\) divide \(c\).
- ★Mostre que, para todo inteiro não-negativo \(n\), o número \(\sqrt n\) é irracional se e somente se \(n\) não é um quadrado perfeito.
- ★Seja \(n\) um inteiro não-negativo e considere a
seguinte afirmação: \(n\) é primo se e somente se \(2^{n}-1\) é primo.
- Prove ou refute a suficiência dessa afirmação.
- Prove ou refute a necessidade dessa afirmação.
- Um inteiro positivo é dito um hiperprimo se possui um número
primo de divisores positivos. Alguns exemplos: \(5\) é um hiperprimo, pois possui
\(2\) divisores positivos (\(1\) e \(5\)); \(4\) é um hiperprimo, pois possui \(3\)
divisores positivos (\(1\), \(2\), e \(4\)); \(81\) é um hiperprimo, pois possui \(5\)
divisores positivos (\(1\), \(3\), \(9\), \(27\), e \(81\)). Sejam
\(\mathbb P\), \(\mathbb H\), e \(\mathbb S\) os conjuntos dos números
primos positivos, hiperprimos, e
quadrados perfeitos, respectivamente. Prove ou refute:
- \(\mathbb H\subseteq \mathbb P\cup\mathbb S\);
- \(\mathbb P\cup \mathbb S\subseteq\mathbb H\).
- ★Seja, como na demonstração do Teorema de Euclides–Euler, \(\sigma(n)\) a soma dos divisores de \(n\), sendo \(n\) qualquer inteiro não-negativo (por exemplo, \(\sigma(6)=12\)). Prove que para quaisquer inteiros positivos coprimos \(a\) e \(b\) vale que \(\sigma(ab)=\sigma(a)\sigma(b)\).
- Prove ou refute:
- É uma relação de ordem parcial sobre \(\bN\) a relação binária \(R\) sobre \(\bN\) tal que \(aRb\) se e somente se \(a\) divide \(b\).
- É uma relação de ordem total sobre \(\bN\) a relação binária \(R\) sobre \(\bN\) tal que \(aRb\) se e somente se \(a\) divide \(b\).
- Seja \(R\) a relação binária sobre \(\mathbb Z\) definida por: \(xRy\) se e somente se \(x+y\) é par. Prove ou refute: \(R\) é uma relação de equivalência.
- ★O fecho transitivo de uma relação binária \(R\) sobre um conjunto
\(A\), denotado por \(R^{+}\), é a menor relação binária que contém \(R\) e que é transitiva,
isto é, é a relação binária transitiva que contém \(R\) e que satisfaz
\(R^{+}\subseteq T\) para qualquer relação binária transitiva \(T\) que
contenha \(R\).
- Calcule o fecho transitivo da relação binária \(R\) sobre \(\{1,2,3,4,5,6,7,8,9,10\}\) tal que \(xRy\) se e somente se \(x\) é um divisor de \(y\).
- Calcule o fecho transitivo da relação binária \(R\) sobre
\(\{a,b,1,2,3,4,5\}\) tal que \(xRy\) se e somente se vale um dos
seguintes casos:
- \(x=a\) e \(y=b\);
- \(x=b\) e \(y=a\);
- \(y=x+1\).
Mostre que
\begin{equation*} R^{+}=\bigcup_{k\geq 1}R^k\,. \end{equation*}- Um subconjunto \(X\) de \(\bN\) é dito contíguo se, para todo \(i\) e todo \(j\) em \(X\) tais que \(j - i\geq 2\), existe algum \(k\in X\) tal que \(i < k < j\). Considere a relação binária sobre um subconjunto contíguo \(X\) de \({\mathbb Z}_{\geq 0}\) dada por: \(xRy\) se e somente se \(y=x+1\). Mostre que existe um inteiro positivo \(t\) tal que \(R^+=\bigcup_{k=1}^t R^k\) se e somente se \(X\) é um conjunto finito.
★Sendo \(\mathcal U\bydef \{ X\mathbin : X\subseteq{\mathbb Z}\}\), seja \(\Delta\) a operação binária sobre \(\mathcal U\) definida por
\begin{equation*} X\Delta Y=\{xy\mathbin : x\in X\text{ e }y\in Y\},\quad\forall X,Y\subseteq\mathbb Z\,. \end{equation*}Por exemplo, \(\{1,2\}\Delta\{1,2,3\}=\{1,2,3,4,6\}\). Seja ainda \(R\) a relação binária sobre \(\mathcal U\) definida por: para \(X,Y\subseteq\mathbb Z\), temos \(XRY\) se e somente se existe \(Z\subseteq\mathbb Z\) tal que \(X\Delta Z=Y\). Prove ou refute: \(R\) é transitiva.
- Seja \(\oplus\) a operação de bitwise XOR ("ou" exclusivo bit a bit) sobre palavras binárias. Por exemplo, \(011\oplus 100\oplus 101=010\). Considere agora o jogo descrito do enunciado do Teorema 2.8, mas generalizado para três pilhas de pedras. Sendo \(x_1\), \(x_2\), e \(x_3\) as codificações em binário das quantidades de pedras nas primeira, segunda, e terceira pilhas, respectivamente, mostre que, supondo que ambos os jogadores jogam otimamente, o vencedor é: o primeiro jogador, se \(x_1\oplus x_2\oplus x_3\) possui algum bit não-nulo; o segundo jogador, se todos os bits de \(x_1\oplus x_2\oplus x_3\) são iguais a \(0\).
- Mostre que um número inteiro é divisível por \(3\) se e somente se a soma dos seus dígitos na base \(10\) é divisível por \(3\).
★Para todo inteiro não-negativo \(n\), mostre por indução em \(n\) que o \(n\)-ésimo número de Fibonacci
\begin{equation*} F_n\equiv 3(8^n-4^n)\pmod {11} \end{equation*}- Alice envia mensagens secretas cifradas em ternário para Bob. Como no código que eles estabeleceram entre eles nunca ocorre um par de \(0\)s consecutivos ou um dígito \(2\) após um dígito \(0\), Alice utiliza o sufixo \(00\) ou \(02\) para marcar o fim da mensagem, situação em que Bob encerra a transmissão imediatamente. Para \(n\geq 2\), seja \(R(n)\) o número de mensagens diferentes de comprimento \(n\) que Alice pode enviar a Bob. Por exemplo, para \(n=3\), temos \(R(n)=4\), pois são \(4\) as possibilidades: \(100\), \(102\), \(200\), e \(202\). Encontre uma fórmula aberta para \(R(n)\) em função de \(n\), explicando todos os passos que conduziram à dedução da fórmula.
★Considere os números inteiros não-negativos dispostos todos na seguinte matriz infinita:
\begin{equation*} \begin{matrix} 0 & 1 & 3 & 6 & 10 & \ldots\\ 2 & 4 & 7 & 11 & \ddots & \\ 5 & 8 & 12 & \ddots & & \\ 9 & 13 & \ddots & &&\\ 14 & \ddots & & &&\\ \vdots& & &&& \end{matrix} \end{equation*}Considerando que as linhas e as colunas dessa matriz são numeradas a partir de \(0\), seja \(\Delta\) a operação binária sobre \(\mathbb Z_{\geq 0}\) tal que, para quaisquer \(i,j\in\mathbb Z_{\geq 0}\), temos que \(i\Delta j\) é o elemento na posição \((i,j)\) da matriz. Por exemplo, \(2\Delta 1=8\).
Apresente uma fórmula aberta para \(i\Delta j\) conforme o modelo:
\begin{equation*} i\Delta j = \left\{ \begin{aligned} &0\,,&&\text{se $i=j=0$;}\\ &\bigl(0\Delta (j-1)\bigr)+(\mathbf{\text{___}})\,,&&\text{se $ j>i=0$;}\\ &\bigl(0\Delta(\mathbf{\text{___}})\bigr)+i\,,&&\text{se $i>0$.} \end{aligned} \right. \end{equation*}Não é necessário justificar sua apresentação.
- Apresente uma fórmula fechada para \(i\Delta j\). Não é necessário justificar sua apresentação.
- Prove por indução em \(j\) que a fórmula apresentada em 27.2 para \(i\Delta j\) quando restrita a \(i=0\) de fato corresponde à fórmula apresentada em 27.1.
- Supondo que a prova apresentada em 27.3 está correta, complete, não necessariamente usando indução, a prova de que a fórmula apresentada em 27.2 de fato corresponde à fórmula apresentada em 27.1.
- Prove ou refute: A operação \(\Delta\) é uma bijeção entre \(\mathbb Z_{\geq 0}^2\) e \(\mathbb Z_{\geq 0}\).
- Considere a variante do Problema das Torres de Hanoi em que são proibidos movimentos diretos entre as torres das extremidades, i.e. movimentos de um prato diretamente da torre \(A\) para a torre \(C\), ou vice-versa. Seja \(T(n)\) o número mínimo de movimentos para se moverem os \(n\) pratos de \(A\) para \(C\). Encontre uma fórmula fechada para \(T(n)\).
★Seja \(X\) o conjunto de inteiros definido recursivamente por:
- \(2\in X\) e \(3\in X\);
- para quaisquer \(a,b\in X\), temos \(a+2b\in X\).
Mostre que \(X={\mathbb Z}_{\geq 2}\setminus\{4,5\}\).
Seja \(S\) o conjunto de pares de inteiros definido recursivamente por:
- \((0,0)\in S\);
- para qualquer \((a,b)\in S\), temos \((a+2,b+3)\in S\) e \((a+3,b+2)\in S\).
Seja também \(X\) o conjunto de inteiros definido recursivamente por:
- \(6\in X\) e \(8\in X\);
- para quaisquer \(a,b\in X\), temos \(a+b\in X\).
Mostre que \(X=\{2n\mathbin : n\in{\mathbb Z}_{\geq 3}\}\setminus\{10\}\) e que \(S\subseteq \{(a,b)\in{\mathbb Z}_{\geq 0}^2\mathbin : a+b\in 5{\mathbb Z}_{\geq 0}\}\). Justifique ainda por que \(S\not\supseteq \{(a,b)\in{\mathbb Z}_{\geq 0}^2\mathbin : a+b\in 5{\mathbb Z}_{\geq 0}\}\).
Considere o seguinte algoritmo, o qual, recebendo \(a\in{\mathbb R}\) e \(n\in{\mathbb Z}_{\geq 0}\), calcula \(a^n\) por exponenciação ternária (ou exponenciação por elevação ao cubo).
\(\underline{\text{ExpTern}(a,n)}\):
- se \(n=0\), devolva \(1\);
- se \(n\) não é múltiplo de \(3\), devolva \(a\cdot \text{ExpTern}(a,n-1)\);
- \(b\leftarrow \text{ExpTern}(a,n/3)\);
- devolva \(b\cdot b\cdot b\).
Mostre que, para quaisquer \(a\in{\mathbb R}\) e \(n\in{\mathbb Z}_{\geq 0}\), o algoritmo \({\text{ExpTern}}(a,n)\) de fato devolve \(a^n\) e, se \(n > 0\), realiza a tarefa executando não mais que \(4\lfloor\log_3 n\rfloor+2\) multiplicações.
★Para \(n,a,b\) inteiros satisfazendo \(1\leq a < b\leq n+1\), considere o seguinte algoritmo, uma aplicação interessante de busca binária.
\(\underline{\text{SqrtFloor}(n,a,b)}\):
- se \(b -a =1\), devolva \(a\);
- \(m\leftarrow \lfloor (a+b)/2\rfloor\);
- se \(m\cdot m\leq n\), devolva \(\text{SqrtFloor}(n,m,b)\);
- devolva \(\text{SqrtFloor}(n,a,m)\).
Mostre, para todo inteiro positivo \(n\), que \(\text{SqrtFloor(n,1,n+1)}\) devolve \(\lfloor\sqrt n\rfloor\), realizando \(O(\log n)\) operações aritméticas.
- Sobre o Algoritmo de Euclides:
- Mostre que o número de chamadas recursivas realizadas por \(\text{Euclides}(F_{n+1},F_{n})\) é exatamente \(n+1\) para todo \(n\in{\mathbb Z}_{\geq 0}\).
- Mostre que o número de chamadas recursivas realizadas por \(\text{Euclides}(a,b)\), para \(a\) e \(b\) inteiros não-negativos quaisquer não ambos iguais a zero satisfazendo \(a\geq b\), é \(O(\log b)\).
Considere a seguinte versão do Algoritmo de Euclides, conhecida também como Algoritmo de Euclides Estendido.
\(\underline{\text{Euclides}(a,b)}\):
- se \(b=0\), devolva \((1,0,a)\);
- \((x,y,d)\leftarrow\text{Euclides}(b, a \bmod b)\);
- devolva \((y, x - y\lfloor a/b\rfloor, d)\).
Mostre que, sendo \(a\) e \(b\) inteiros não-negativos não sendo ambos iguais a zero, e sendo \((x,y,d)\bydef{\text{Euclides}(a,b)}\), temos que \(d=\gcd(a,b)\) e que \((x,y)\) é uma solução de equação diofantina
\begin{equation*} ax + by = d\,. \end{equation*}- Ana Maria foi à feira comprar bananas e maçãs para fazer uma torta. As bananas estavam custando R$ 0,22 cada, enquanto que as maçãs, R$ 0,98 cada. Ana Maria gastou R$ 5,36 e não comprou nada além de bananas e maçãs. Quantas bananas e quantas maçãs ela comprou? Justifique sua resposta.
- ★Encontre uma fórmula fechada para o número \(R(n)\) de mensagens diferentes de comprimento \(n\) que Alice pode enviar a Bob, conforme o Exercício 26, explicando todos os passos que conduziram à dedução da fórmula. Exiba ainda um algoritmo que, realizando \(O(\log n)\) operações aritméticas com inteiros, calcula \(R(n)\), explicando todos os passos que conduziram à dedução do algoritmo.
- Só se pode entrar na bela cidade da Nlogônia com um veículo oficial
da frota da rainha, o qual pode ser um ônibus ou um micro-ônibus. Os
ônibus e os micro-ônibus oficiais possuem \(2\) e \(1\) Nlogômetros de
comprimento, respectivamente. Os micro-ônibus podem ser apenas da
cor verde; já os ônibus podem ser azuis ou vermelhos. Dois veículos
da mesma cor são indistinguíveis. Só se entra na cidade pela Ponte
da Recorrência, a qual mede \(n\geq 0\) Nlogômetros de comprimento e
possui só uma pista. Quando alguém quer sair da Nlogônia, precisa
tomar outra ponte. Para entrar na Ponte da Recorrência, um veículo
sempre deve aguardar haver espaço para que ele caiba completamente
sobre ela. Para sair da ponte e entrar na cidade, um veículo deve
aguardar a autorização do oficial real, e, quando isto acontece, o
veículo deve sair completamente da ponte. Todo veículo que está
sobre a ponte deve ficar posicionado o mais para frente
possível. Seja \(F(n)\) o número de filas diferentes, em função de
\(n\), que se pode ter na ponte quando ela está lotada. Por exemplo,
para \(n=2\), temos \(3\) possibilidades: ou há dois micro-ônibus na
ponte, ou um ônibus azul, ou um ônibus vermelho. Para \(n=3\), temos
\(5\) possibilidades.
- Encontre uma fórmula aberta (recorrente) para \(F(n)\) em função de \(n\). Descreva todos os passos que levaram você à dedução da fórmula.
Deduza uma fórmula fechada (não-recorrente) para \(F(n)\) em função de \(n\), conforme o modelo. Demonstre todos os passos que levaram você à dedução da fórmula.
\begin{equation*} F(n) =\left\{ \begin{aligned} &\frac{2^{(\mathbf{\text{___}})}+(\mathbf{\text{___}})}3\,,&&\text{se $n$ é par;}\\ &\frac{2^{(\mathbf{\text{___}})}+(\mathbf{\text{___}})}3\,,&&\text{se $n$ é ímpar.} \end{aligned} \right. \end{equation*}
- Considere a sequência numérica obtida a partir dos inteiros
positivos permutando-se cada par \((i,i+1)\) em que \(i\) é ímpar,
i.e. \(2,1,4,3,6,5,8,7,\dotsc\). Seja \(a_i\) o \(i\)-ésimo termo dessa
sequência, para \(i\geq 1\), i.e. \(a_1=2\), \(a_2=1\) etc.
- Escreva uma recorrência linear homogênea com coeficientes constantes para \(a_i\) para \(i\geq 4\). Não é necessário justificar sua recorrência.
- Encontre uma fórmula fechada para \(a_i\) apresentando todos os passos da dedução, conforme os teoremas vistos em aula.
- Sendo \(F_n\) o \(n\)-ésimo número de Fibonacci, mostre que, à medida que \(n\) cresce, a razão \(F_{n+1}/F_n\) converge para o número \(\upphi\).
★Um rajá deixou como herança para suas \(n \geq 2\) filhas um conjunto de pérolas e determinou que a partilha das pérolas seria feita por ordem decrescente de idade da seguinte maneira: a primeira filha receberia uma pérola e mais um sétimo do que restasse, a segunda filha receberia duas pérolas e mais um sétimo do que restasse, e assim por diante, até a filha mais nova. Achando injusta a determinação do pai, as filhas foram à Justiça, mas o juiz observou que, seguindo à risca as instruções deixadas pelo rajá, todas as filhas receberiam exatamente a mesma quantidade de pérolas. Quantas filhas o rajá tinha e quantas pérolas cada uma recebeu?
Para resolver este exercício, siga o seguinte roteiro:
- Sendo \(n\) o número de filhas, seja \(a_0\) a quantidade inicial de pérolas e, para \(0 < i \leq n\), seja \(a_i\) a quantidade de pérolas restantes após a \(i\)-ésima filha tomar sua parte. Escreva uma recorrência para \(a_i\) para \(i > 0\).
- Como, conforme observado pelo juiz, cada filha acabou recebendo exatamente a mesma quantidade de pérolas, podemos afirmar que a sequência \(a_0,a_1,\dotsc,a_n\) é uma progressão \(\mathbf{\text{_______}}\). Sendo \(d\) a razão dessa progressão, escreva uma fórmula fechada para \(a_i\), para \(0\leq i\leq n\), em função de \(d\) e \(i\). Em seguida, usando essa fórmula e as propriedades que toda progressão \(\mathbf{\text{_______}}\) satisfaz, encontre \(d\), e depois \(n\).
Obtenha uma resolução alternativa para este exercício usando o fato de que toda progressão \(\mathbf{\text{_______}}\) satisfaz a recorrência
\begin{equation*} a_n = (\mathbf{\text{___}})a_{n-1} - a_{n-2}\,. \end{equation*}
★Exiba o pseudocódigo de um algoritmo que, recebendo \(T\in{\mathbb Z}_{> 0}\) e \(N\in{\mathbb Z}_{\geq 0}\), devolve o valor de
\begin{equation*} f(N, T) = \frac1{i\sqrt{4T-1}}\Bigl( \Bigl(\frac{1+i\sqrt{4T-1}}2\Bigr)^N- \Bigl(\frac{1-i\sqrt{4T-1}}2\Bigr)^N \Bigr) \end{equation*}Seu algoritmo só pode realizar operações aritméticas envolvendo inteiros e o número de tais operações deve ser \(O(\log N)\).
Uma sequência \((a_n)_{n\geq 0}\) satisfaz as seguintes propriedades:
- os primeiros quatro termos (\(a_0,a_1,a_2,a_3\)) são \(1,-2,3,-4\);
- para \(n\geq 2\), \(a_n\) satisfaz uma recorrência linear homogênea de ordem \(2\).
Assim,
- Encontre a recorrência linear homogênea de ordem \(2\) para \(a_n\) para \(n\geq 2\).
- Encontre uma fórmula fechada para \(a_n\).
- Qual o menor inteiro \(N\) que garante que sempre que \(N\) inteiros forem escolhidos no intervalo \([2..200]\), seguramente haverá dois inteiros escolhidos \(a,b\) tais que \(a\) divide \(b\)?
- Vamos organizar uma fila com 4 crianças, 8 adultos, e 4 idosos. As
crianças devem estar todas juntas na fila, à possível exceção de 1
adulto que pode estar entre duas elas. Os adultos devem estar todos
juntos, exceto por um deles, que pode estar entre duas das crianças. Os
idosos devem estar todos juntos e, se o grupo dos idosos não for o
primeiro da fila, então o grupo dos idosos deve vir imediatamente
após o grupo das crianças. Quantas maneiras há de se organizar essa
fila:
- considerando pessoas do mesmo grupo (crianças, adultos, idosos) distinguíveis entre si?
- considerando pessoas do mesmo grupo (crianças, adultos, idosos) indistinguíveis entre si?
Mostre que, sendo \(n\) e \(m\) inteiros não-negativos coprimos, a sequência
\begin{equation*} 0\bmod m, n\bmod m, 2n\bmod m, 3n\bmod m,\dotsc,(m-1)n\bmod m \end{equation*}é uma permutação dos inteiros \(0,1,2,\dotsc,m-1\).
Sendo \(n\in\bN\), o Princípio da Inclusão–Exclusão para \(n\) conjuntos é a asserção de que, sendo \(\mathcal F\) uma família de \(n\) conjuntos finitos,
\begin{equation*} \Bigl\lvert \bigcup_{X\in\mathcal F} X\Bigr\rvert = \sum_{k = 1}^n(-1)^{k - 1}\sum_{\mathcal S\in\binom{\mathcal F}{k}} \Bigl\lvert \bigcap_{X\in\mathcal S}X\Bigr\rvert\,. \end{equation*}- Prove o Princípio da Inclusão–Exclusão para \(n\) conjuntos.
- Uma prova com três questões foi aplicada a uma turma com \(150\) estudantes, dos quais: \(60\) acertaram a primeira questão; \(80\) acertaram a segunda questão; \(90\) acertaram a terceira questão. Sabendo que todo estudante acertou pelo menos uma questão e que \(10\) estudantes acertaram as três questões, quantos estudantes acertaram só uma questão, e quantos acertaram exatamente duas questões?
- Para quaisquer inteiros não-negativos \(n\) e \(k\) tais que \(n \geq k\):
- mostre que, se \(n > k\), então \(n\cdot n^{\underline k}=n^{\underline{k+1}}+kn^{\underline k}\);
usando o item anterior, mostre por indução que, se \(n\) e \(k\) não são ambos iguais a zero, então
\begin{equation*} n^k = \sum_{i= 0}^k\stirling{k}{i}n^{\underline i}\,. \end{equation*}
Para \(n,k\in\bN\) satisfazendo \(0\leq k\leq n\), mostre por indução a fórmula fechada para o número de Stirling do segundo tipo:
\begin{equation*} \stirling n k =\frac1{k!}\sum_{i=0}^k(-1)^i\binom k i(k-i)^n\,. \end{equation*}- ★Sendo \(n,k\in\bN\), seja \(F(n,k)\) o número de maneiras de distribuir
\(n\) bolas para \(k\) caixas. Encontre uma fórmula (fechada usando os
conceitos estudados na aula, ou aberta) para \(F(n,k)\) nos casos em
que:
- as bolas são distinguíveis e as caixas são distinguíveis;
- as bolas são indistinguíveis e as caixas são distinguíveis;
- as bolas são distinguíveis e as caixas são indistinguíveis;
- as bolas são indistinguíveis e as caixas são indistinguíveis.
- ★Mostre que o número de sobrejeções de um conjunto finito \(A\) em um conjunto finito \(B\) é: \(0\) se \(\lvert A\rvert < \lvert B\rvert\); \(\stirling{\lvert A\rvert}{\lvert B\rvert}\lvert B\rvert!\) se \(\lvert A\rvert\geq\lvert B\rvert\).
Seja \(n\) um inteiro não-negativo e sejam \(k_1,k_2,\dotsc,k_m\) uma sequência de \(m\) inteiros não-negativos tais que \(k_1+k_2+\dotsb+k_m=n\). Mostre que o número de maneiras de distribuir \(n\) bolas distinguíveis para \(m\) caixas distinguíveis de modo que a \(i\)-ésima caixa receba exatamente \(k_i\) bolas é dado pelo coeficiente multinomial
\begin{equation*} \binom{n}{k_1,k_2,\dotsc,k_m}=\frac{n!}{k_1!k_2!\dotsb k_m!}\,. \end{equation*}- De quantas maneiras diferentes podem se sentar \(11\) homens e \(8\) mulheres em uma fileira sem que duas mulheres se sentem juntas?
- Um grupo de 15 crianças viaja sempre no mesmo ônibus \(A\) para ir e para
voltar da escola. Na frente (assentos de 1 a 6) sempre senta
Rita. No meio (assentos de 7 a 11) sempre senta Martin. Atrás (assentos de
12 a 15) sempre senta Rosa. As demais crianças podem sentar em
qualquer assento.
- De quantas maneiras diferentes esse ônibus pode viajar?
- Agora, 12 crianças mudaram de escola, e somente Rita, Martin, e Rosa é que viajam no ônibus \(A\). De quantas maneiras diferentes esse ônibus pode viajar?
- As filas dos assentos da frente têm 3 assentos cada. As filas dos assentos do meio têm 1 assento cada. As filas dos assentos de trás tem 2 assentos cada. Agora, cada criança pode ocupar qualquer número positivo de assentos de uma mesma fila, pois, aproveitando que são só elas no ônibus, elas às vezes deitam sobre os assentos. De quantas maneiras diferentes esse ônibus pode viajar, considerando que se uma criança ocupa um número maior que um de assentos, é indistinguível a orientação na qual a criança deita?
- Quantos anagramas possui o código genético ATGCGAGTC em que não haja ocorrências de uma mesma base (A, T, C, G) em posições adjacentes?
- Quantos anagramas sem zeros à esquerda possui o número \(743092\) que sejam múltiplos de \(11\)?
★Ana possui \(N\) unidades de um dado de \(F\) faces, as quais são numeradas de \(1\) a \(F\) (ao ser lançado, o dado pode assumir qualquer um desses valores, que é o que fica voltado para cima). Ana coloca os \(N\) dados em um copo e os lança sobre a mesa. Veja que, num lançamento, não importa a ordem dos dados. Assim, um lançamento de \(4\) dados que resulte nos valores \(1\), \(5\), \(2\), \(1\) é idêntico ao lançamento que resulta nos valores \(2\), \(1\), \(1\), \(5\). Veja também que, neste lançamento, apesar de serem \(4\) dados, há somente \(3\) valores distintos aparecendo: \(1\), \(2\), \(5\).
Sendo \(K\) um inteiro positivo tal que \(K \leq F\) e \(K \leq N\), quantos lançamentos diferentes há que resultem em exatamente \(K\) valores distintos?
★Uma prova de Matemática Discreta possui \(3\) questões. O estudante pode escolher o valor para cada uma das questões desde que:
- as escolhas sejam todas números inteiros;
- a soma dos valores das \(3\) questões seja exatamente \(100\);
- o valor de cada questão seja pelo menos \(15\) e no máximo \(45\).
De quantas maneiras diferentes o estudante pode escolher os valores das questões?
Um resultado clássico da Combinatória é que o número de expressões bem formadas por \(n\) pares de parênteses pode ser dado pelo \(n\)-ésimo número de Catalan, o qual admite a fórmula aberta:
\begin{equation} C_n = \left\{ \begin{aligned} & 1\,,&&\text{se $n=0$;}\\ & \frac{2(2n-1)}{n+1}C_{n-1}\,,&&\text{se $n > 0$.} \end{aligned} \right. \end{equation}Por exemplo, \((C_0,C_1,C_2,C_3,C_4,C_5)=(1,1,2,5,14,42)\), e as \(C_3=5\) expressões bem formadas por \(3\) pares de parênteses são: $ ((()))$; \((())()\); \(()(())\); \((()())\); \(()()()\).
Mostre que para todo inteiro positivo \(n\),
\begin{equation*} \binom{2n-1}{n}=\binom{2n-1}{n-1}\,. \end{equation*}Mostre por indução que, para todo inteiro não-negativo \(n\),
\begin{equation*} C_n = \frac{1}{n+1}\binom{2n}{n}\,. \end{equation*}
- ★Sendo \(n\) um inteiro não-negativo, seja \(A(n)\) o número máximo de regiões que é possível criar no interior de uma circunferência ao dispor sobre ela \(n\) pontos, conectando-os todos dois a dois por um segmento de reta. Encontre uma fórmula fechada para \(A(n)\) em função de \(n\), provando que a fórmula está correta.
- O Rei da Nlogônia quer determinar que \(k\) de seus \(n\geq 1\) súditos sejam enviados para uma expedição ao Além-mar em dois navios, Prometheus e Kerberos, que devem partir não-vazios. Para \(1\leq k\leq n\), seja \(R(n, k)\) o número de maneiras diferentes para a determinação do Rei. Considere que os súditos são distinguíveis, bem como os dois navios, mas que os lugares que os súditos ocupam dentro nos navios são indistinguíveis, até porque os súditos podem passear dentro do navio. Por exemplo, \(R(4,3)=24\). Escreva uma fórmula fechada para \(R(n, k)\), explicando como você chegou à fórmula. A fórmula pode ser expressa utilizando elementos de notação vistos em aula, como \(n^{\underline k}\), \(\binom n k\), \(\stirling n k\) etc.
- Carlos e sua esposa deram um jantar a outros três casais. Durante o jantar, houve vários apertos de mão. Ninguém apertou a própria mão, e ninguém apertou a mão do próprio cônjuge. Ao final do jantar, Carlos perguntou a todos quantas mãos cada um havia apertado, e obteve de cada um uma resposta diferente. Quantas mãos Carlos apertou? Quantas mãos a esposa de Carlos apertou? Justifique sua resposta.
- Quantos grafos não isomorfos existem com \(6\) vértices e \(4\) arestas? Exiba-os todos.
- Mostre que um grafo \(d\)-regular com \(n\) vértices não pode ter ambos \(d\) e \(n\) ímpares.
- ★Mostre que todo grafo com grau mínimo \(\delta\) possui um caminho de comprimento \(\delta\) e, se \(\delta \geq 2\), um ciclo de comprimento pelo menos \(\delta + 1\).
- ★Uma folha em uma árvore \(T\) é um vértice com grau \(1\).
- Prove que toda árvore possui ao menos uma folha (dica: use o Exercício 63).
- Prove que toda árvore \(T\) possui ao menos \(\Delta(T)\) folhas (dica: use o item anterior).
O grafo \(G\) abaixo não é um grafo bipartido. Exiba um subgrafo de \(G\) que: seja bipartido; tenha o mesmo grau máximo que o de \(G\); tenha o maior número possível de vértices e arestas.
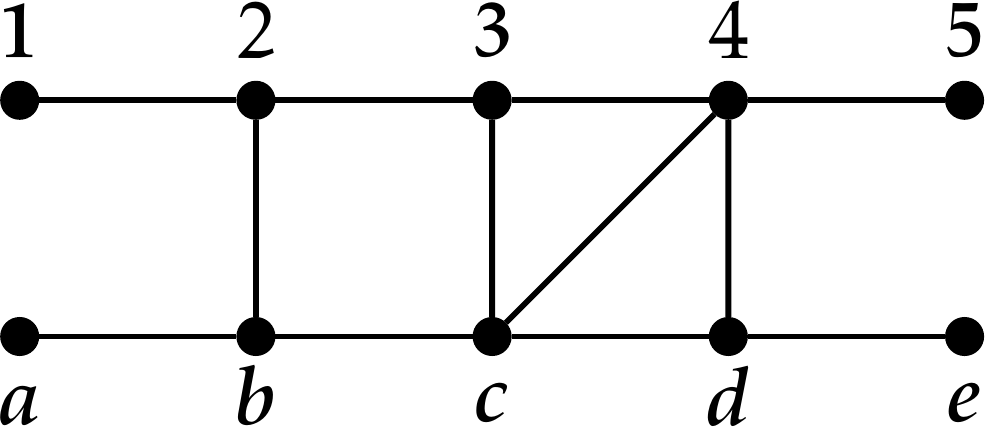
- Mostre que o número de arestas de toda árvore com \(n\geq 1\) vértices é exatamente \(n - 1\).
- Seja \(X\) o conjunto dos vértices de grau máximo de um grafo \(G\) qualquer. Mostre que se \(X\) induz um grafo acíclico em \(G\), então, \(V(G)\setminus X\) tem pelo menos \(\Delta(G)-1\) vértices.
- Sobre isomorfismo de grafos.
Os grafos abaixo são isomorfos? Justifique sua resposta.
Os grafos abaixo são isomorfos? Justifique sua resposta.
- Sobre o grafo de Petersen:
- ele é uma árvore?
- ele é um grafo bipartido?
- qual a cardinalidade de sua maior clique?
- qual a cardinalidade de seu maior conjunto independente?
- Um grafo é dito planar quando pode ser representado no
plano sem que as arestas se cruzem.
- Mostre que o \(K_4\) é planar.
- Quantos grafos não-isomorfos regulares planares e conexos com seis vértices existem? Exiba-os, representando-os no plano de modo a evidenciar sua planaridade.
★Na rede social que você criou, quando uma pessoa \(A\) adiciona uma pessoa \(B\) como amigo, tanto \(A\) aparece na lista de amigos de \(B\), quanto \(B\) aparece na lista de amigos de \(A\). Por enquanto, sua rede social possui só \(5\) usuários: Alice, Bob, Clara, Dora, e Eve. Porém, ninguém adicionou ninguém como amigo ainda, pois cada um apenas criou sua conta e não logou mais. Para movimentar sua rede social, você quer, usando seus superpoderes administrativos, estabelecer alguns relacionamentos de amizade (Sim, quando algum dos usuários logar novamente, vai ver alguns amigos que não foi ele que adicionou!), criando o menor número possível de relacionamentos de modo que o grafo da rede social se torne conexo. De quantas maneiras você pode criar esses relacionamentos atendendo às restrições do enunciado, e por que a resposta é \(125\)? Abaixo estão representadas todas as \(5\) dessas \(125\) maneiras em que existe um usuário que é amigo de todos os outros, representando cada usuário pela inicial do seu nome.
